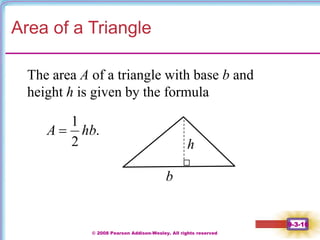
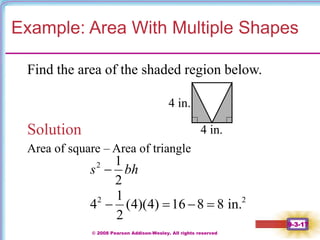
This document contains notes on perimeter, area, and circumference from a geometry textbook chapter. It defines perimeter as the distance around a shape and area as the surface covered. Formulas are provided for calculating the perimeter and area of polygons like triangles, rectangles, squares, parallelograms, and trapezoids. Circumference is defined as the distance around a circle, and formulas show circumference is equal to pi times the diameter or twice pi times the radius. The area of a circle is equal to pi times the radius squared. Examples demonstrate calculating perimeter, area, and circumference for various shapes.

1. Chapter 9
Geometry
© 2008 Pearson Addison-Wesley.
All rights reserved

2. © 2008 Pearson Addison-Wesley. All rights reserved
9-3-2
Chapter 9: Geometry
9.1 Points, Lines, Planes, and Angles
9.2 Curves, Polygons, and Circles
9.3 Perimeter, Area, and Circumference
9.4 The Geometry of Triangles: Congruence,
Similarity, and the Pythagorean Theorem
9.5 Space Figures, Volume, and Surface Area
9.6 Transformational Geometry
9.7 Non-Euclidean Geometry, Topology, and Networks
9.8 Chaos and Fractal Geometry

3. © 2008 Pearson Addison-Wesley. All rights reserved
9-3-3
Chapter 1
Section 9-3
Perimeter, Area, and Circumference

4. © 2008 Pearson Addison-Wesley. All rights reserved
9-3-4
Perimeter, Area, and Circumference
• Perimeter of a Polygon
• Area of a Polygon
• Circumference of a Circle
• Area of a Circle

5. © 2008 Pearson Addison-Wesley. All rights reserved
9-3-5
Perimeter of a Polygon
The perimeter of any polygon is the sum of
the measures of the line segments that form its
sides. Perimeter is measured in linear units.

6. © 2008 Pearson Addison-Wesley. All rights reserved
9-3-6
Perimeter of a Triangle
a
b
c
The perimeter P of a triangle with sides of
lengths a, b, and c is given by the formula
P = a + b + c.

7. © 2008 Pearson Addison-Wesley. All rights reserved
9-3-7
Perimeter of a Rectangle
The perimeter P of a rectangle with length l
and width w is given by the formula
P = 2l + 2w,
or equivalently
P = 2(l + w).
w
l

8. © 2008 Pearson Addison-Wesley. All rights reserved
9-3-8
Perimeter of a Square
The perimeter P of a square with all sides of
length s is given by the formula
P = 4s.
s
s

9. © 2008 Pearson Addison-Wesley. All rights reserved
9-3-9
Area of a Polygon
The amount of plane surface covered by a
polygon is called its area. Area is measured
in square units.

10. © 2008 Pearson Addison-Wesley. All rights reserved
9-3-10
Area of a Rectangle
The area A of a rectangle with length l and
width w is given by the formula
A = lw.
w
l

11. © 2008 Pearson Addison-Wesley. All rights reserved
9-3-11
Example: Rectangle
Find the perimeter and area of the rectangle
below.
7 ft.
15 ft.
Solution
P = 2l + 2w = 2(15) + 2(7) = 44 ft.
Perimeter
Area
A = lw = 15(7) = 105 ft.2

12. © 2008 Pearson Addison-Wesley. All rights reserved
9-3-12
Area of a Square
The area A of a square with all sides of
length s is given by the formula
P = s2.
s
s

13. © 2008 Pearson Addison-Wesley. All rights reserved
9-3-13
Area of a Parallelogram
The area A of a parallelogram with height h
and base b is given by the formula
A = bh.
b
h

14. © 2008 Pearson Addison-Wesley. All rights reserved
9-3-14
Area of a Trapezoid
The area A of a trapezoid with parallel bases
b and B and height h is given by the formula
B
h
b
 
1
.
2
A h B b
 

15. © 2008 Pearson Addison-Wesley. All rights reserved
9-3-15
Example: Area of a Parallelogram
Find the area of the trapezoid below.
Solution
13 cm.
5 cm.
7 cm.
   
1 1
(5) 7 13
2 2
A h B b
   
  2
1
(5) 20 50 cm.
2
 

16. © 2008 Pearson Addison-Wesley. All rights reserved
9-3-16
Area of a Triangle
The area A of a triangle with base b and
height h is given by the formula
h
b
1
.
2
A hb


17. © 2008 Pearson Addison-Wesley. All rights reserved
9-3-17
Example: Area With Multiple Shapes
Find the area of the shaded region below.
Solution
Area of square – Area of triangle
2 1
2
s bh

4 in.
4 in.
2 2
1
4 (4)(4) 16 8 8 in.
2
   

18. © 2008 Pearson Addison-Wesley. All rights reserved
9-3-18
Circumference of a Circle
The distance around a circle is called its
circumference.

19. © 2008 Pearson Addison-Wesley. All rights reserved
9-3-19
Circumference of a Circle
The circumference C of a circle of diameter d
is given by the formula.
or equivalently
where r is a radius.
,
C d


2 ,
C r


d
r

20. © 2008 Pearson Addison-Wesley. All rights reserved
9-3-20
Area of a Circle
The area A of a circle with radius r is given
by the formula.
2
.
A r


r

21. © 2008 Pearson Addison-Wesley. All rights reserved
9-3-21
Example: Circle
Find the area and circumference of a circle
with a radius that is 6 inches long (use 3.14
as an approximation for pi).
Solution
2 2 (6) 12 37.68 in.
C r
  
   
Circumference
Area
2 2 2
(6) 36 113.04 in.
A r
  
   