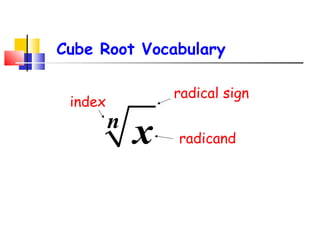
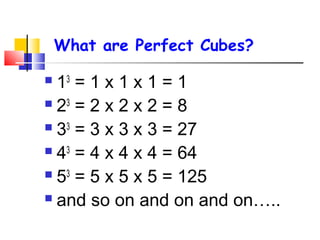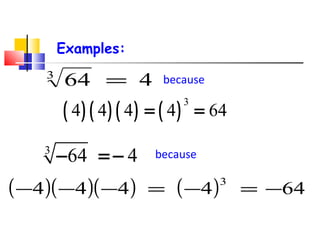The cube root of a number is the value that when multiplied by itself three times equals the original number. Some numbers have exact cube roots, called perfect cubes, which can be written as the cube of another number, such as 64 = 43. Not all numbers have exact cube roots. Cube roots can sometimes be simplified by writing the number as a product with one factor being a perfect cube and extracting that root, leaving the remaining factor under the radical.

1. The index of a cube root is
always 3.
The cube root of 64 is written as
.3
64
Cube Roots

2. What does cube root mean?
The cube root of a number is…
…the value when multiplied by itself
three times gives the original number.

3. Cube Root Vocabulary
n
x
index
radicand
radical sign

4. If a number is a perfect cube, then
you can find its exact cube root.
A perfect cube is a number that can
be written as the cube (raised to
third power) of another number.
Perfect Cubes

5. What are Perfect Cubes?
 13
= 1 x 1 x 1 = 1
 23
= 2 x 2 x 2 = 8
 33
= 3 x 3 x 3 = 27
 43
= 4 x 4 x 4 = 64
 53
= 5 x 5 x 5 = 125
 and so on and on and on…..

6. Examples:
( ) ( ) ( ) ( )
3
4 4 4 4 64= =
4643
=
because
( )( )( ) ( ) 644444
3
−=−=−−−
because
3
64 4− = −

7. Examples:
3
327 =
3
5
4
125
64






=
3
6216 =
3273
=
5
4
125
643 =
62163
=

8. Examples:
( )33
28 aa =
( )3515
464 yy −=−
( )3412
327 mm =
aa 283 3
=
53 15
464 yy −=−
43 12
327 mm =

9. Not all numbers or expressions have
an exact cube root as in the previous
examples.
If a number is NOT a perfect cube,
then you might be able to SIMPLIFY it.
Simplify Cube Roots

10. 2 Extract the cube root of the
factor that is a perfect cube.
1 Write the radicand as a product of
two factors, where one of the
factors is a perfect cube.
To simplify a cube root ...
3 The factors that are not perfect
cubes will remain as the radicand.

11. perfect cube
Examples:
=⋅3
227 3
23
3 36 3 2
125 4× =a b ab 3 22
45 abba
3
1043
64 10× =
3 36 3 23
125 4× × × =a a b b
=3
541)
=3
6402)
3 7 5
500 =a b3)

12. Not all cube roots
can be simplified!
• 30 is not a perfect cube.
• 30 does not have a perfect
cube factor.
Example: 3
30
cannot be simplified!
3
30