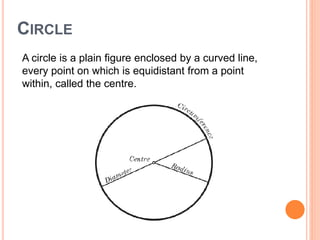
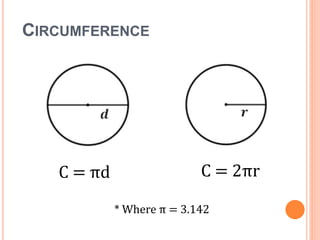
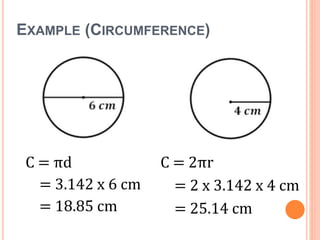
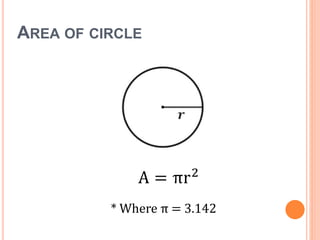
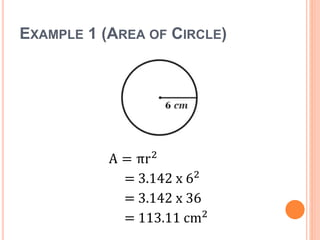
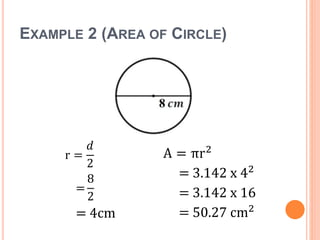
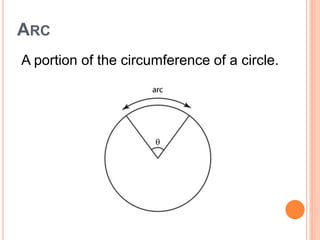
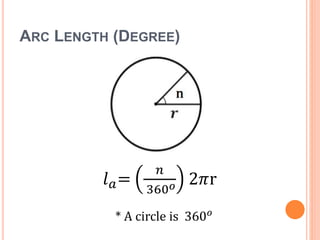
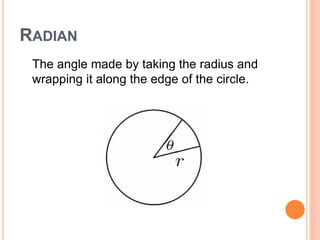
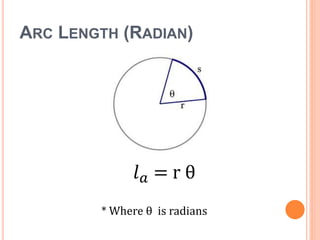
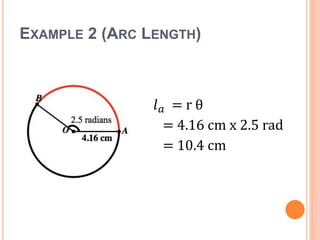
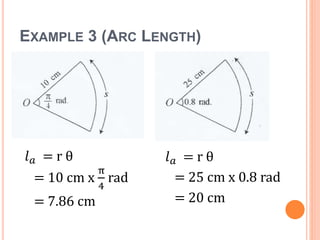
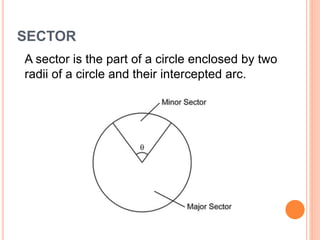
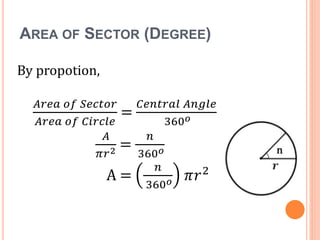
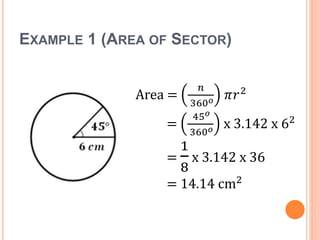
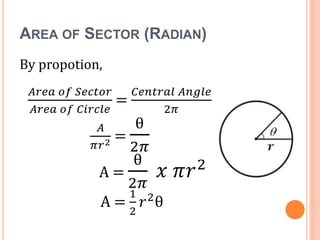
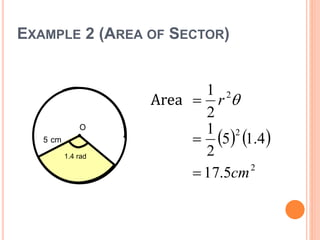
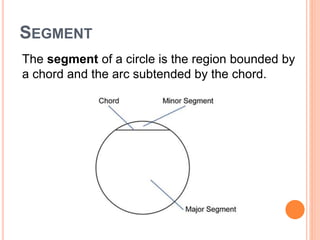
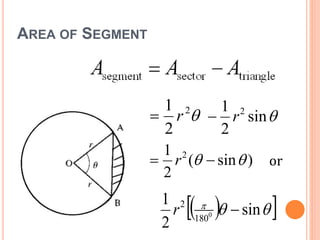
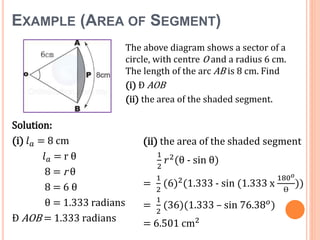
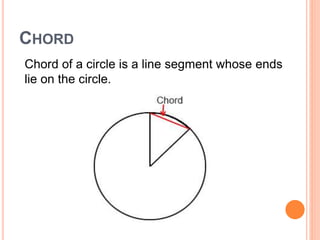
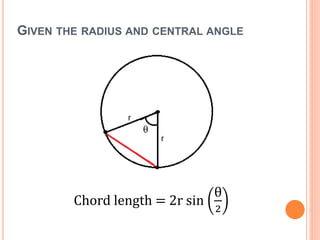
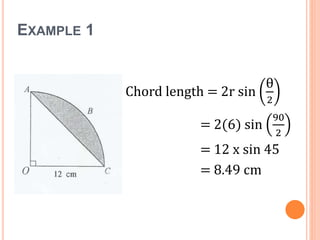
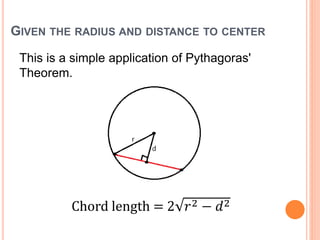
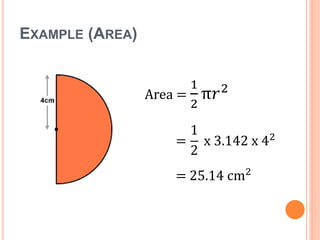
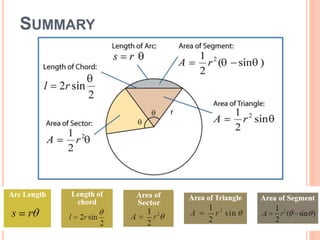
This document defines key terms and formulas related to circles, including circumference, diameter, radius, area, arcs, sectors, segments, chords, and semicircles. It provides formulas for calculating the circumference, area, arc length, area of sectors and segments, chord length, perimeter and area of semicircles. Examples are included to demonstrate how to apply the formulas to solve geometry problems involving circles.

1. CIRCLE
Prepared by : Pang Kai Yun, Sam Wei Yin,
Ng Huoy Miin, Trace Gew Yee,
Liew Poh Ka, Chong Jia Yi

2. CIRCLE
A circle is a plain figure enclosed by a curved line,
every point on which is equidistant from a point
within, called the centre.

3. DEFINITION
Circumference - The circumference of a
circle is the perimeter
Diameter - The diameter of a circle is longest
distance across a circle.
Radius - The radius of a circle is the distance
from the center of the circle to the outside
edge.

4. CIRCUMFERENCE
C = 2πrC = πd
* Where π = 3.142

5. EXAMPLE (CIRCUMFERENCE)
C = πd
= 3.142 x 6 cm
= 18.85 cm
C = 2πr
= 2 x 3.142 x 4 cm
= 25.14 cm

6. AREA OF CIRCLE
* Where π = 3.142
A = πr2

7. EXAMPLE 1 (AREA OF CIRCLE)
A = πr2
= 3.142 x 62
= 3.142 x 36
= 113.11 cm2

8. EXAMPLE 2 (AREA OF CIRCLE)
A = πr2
= 3.142 x 42
= 3.142 x 16
= 50.27 cm2
r =
𝑑
2
=
8
2
= 4cm

9. ARC
A portion of the circumference of a circle.

10. ARC LENGTH (DEGREE)
𝑙 𝑎=
𝑛
360 𝑜 2𝜋r
* A circle is 360 𝑜

11. EXAMPLE 1 (ARC LENGTH)
𝑙 𝑎 =
𝑛
360 𝑜 2𝜋r
=
45 𝑜
360 𝑜 x 2 x 3.142 x 12
=
1
8
x 75.41
= 9.43 cm

12. RADIAN
The angle made by taking the radius and
wrapping it along the edge of the circle.

13. FROM RADIAN TO DEGREE
Degree =
180 𝑜
π
x Radians
Radians =
π
180 𝑜 x Degree
FROM DEGREE TO RADIAN

14. EXAMPLE (FROM DEGREE TO RADIAN)
1. 30 𝑜
=
π
180 𝑜 x 30 𝑜
=
π
6
rad
3. 270 𝑜
=
π
180 𝑜 x 270 𝑜
=
3π
2
rad
2. 150 𝑜
=
π
180 𝑜 x 150 𝑜
=
5π
6
rad

15. EXAMPLE (FROM RADIAN TO DEGREE)
1.
π
3
rad =
180 𝑜
π
x
π
3
rad = 60 𝑜
2.
2π
3
rad =
180 𝑜
π
x
2π
3
rad = 120 𝑜
3.
5π
4
rad =
180 𝑜
π
x
5π
4
rad = 225 𝑜

16. ARC LENGTH (RADIAN)
𝑙 𝑎 = r θ
* Where θ is radians

17. EXAMPLE 2 (ARC LENGTH)
𝑙 𝑎 = r θ
= 4.16 cm x 2.5 rad
= 10.4 cm

18. EXAMPLE 3 (ARC LENGTH)
𝑙 𝑎 = r θ
= 10 cm x
π
4
rad
= 7.86 cm
𝑙 𝑎 = r θ
= 25 cm x 0.8 rad
= 20 cm

19. SECTOR
A sector is the part of a circle enclosed by two
radii of a circle and their intercepted arc.

20. AREA OF SECTOR (DEGREE)
𝐴𝑟𝑒𝑎 𝑜𝑓 𝑆𝑒𝑐𝑡𝑜𝑟
𝐴𝑟𝑒𝑎 𝑜𝑓 𝐶𝑖𝑟𝑐𝑙𝑒
=
𝐶𝑒𝑛𝑡𝑟𝑎𝑙 𝐴𝑛𝑔𝑙𝑒
360 𝑜
𝐴
𝜋𝑟2 =
𝑛
360 𝑜
A =
𝑛
360 𝑜 𝜋𝑟2
By propotion,

21. EXAMPLE 1 (AREA OF SECTOR)
Area =
𝑛
360 𝑜 𝜋𝑟2
=
45 𝑜
360 𝑜 x 3.142 x 62
=
1
8
x 3.142 x 36
= 14.14 cm2

22. AREA OF SECTOR (RADIAN)
𝐴𝑟𝑒𝑎 𝑜𝑓 𝑆𝑒𝑐𝑡𝑜𝑟
𝐴𝑟𝑒𝑎 𝑜𝑓 𝐶𝑖𝑟𝑐𝑙𝑒
=
𝐶𝑒𝑛𝑡𝑟𝑎𝑙 𝐴𝑛𝑔𝑙𝑒
2𝜋
𝐴
𝜋𝑟2 =
θ
2𝜋
A =
θ
2𝜋
𝑥 𝜋𝑟2
A =
1
2
𝑟2
θ
By propotion,

23. EXAMPLE 2 (AREA OF SECTOR)
Area
5 cm
O
1.4 rad
2
2
1
r
   
2
2
5.17
4.15
2
1
cm


24. SEGMENT
The segment of a circle is the region bounded by
a chord and the arc subtended by the chord.

25. AREA OF SEGMENT
2
2
1
r sin
2
1 2
r
)sin(
2
1 2
  r
  
sin
2
1
0
180
2
r
or

26. EXAMPLE (AREA OF SEGMENT)
Solution:
(i) 𝑙 𝑎 = 8 cm
𝑙 𝑎 = r θ
8 = r θ
8 = 6 θ
θ = 1.333 radians
Ð AOB = 1.333 radians
The above diagram shows a sector of a
circle, with centre O and a radius 6 cm.
The length of the arc AB is 8 cm. Find
(i) Ð AOB
(ii) the area of the shaded segment.
(ii) the area of the shaded segment
1
2
𝑟2(θ - sin θ)
=
1
2
(6)2(1.333 - sin (1.333 x
180 𝑜
ϴ
))
=
1
2
(36)(1.333 – sin 76.38 𝑜
)
= 6.501 cm2

27. CHORD
Chord of a circle is a line segment whose ends
lie on the circle.

28. GIVEN THE RADIUS AND CENTRAL ANGLE
Chord length = 2r sin
θ
2

29. EXAMPLE 1
Chord length = 2r sin
θ
2
= 2(6) sin
90
2
= 12 x sin 45
= 8.49 cm

30. GIVEN THE RADIUS AND DISTANCE TO CENTER
This is a simple application of Pythagoras'
Theorem.
Chord length = 2 𝑟2 − 𝑑2

31. EXAMPLE 2
Find the chord of the circle where the radius
measurement is about 8 cm that is 6 units from the
middle.
Solution:
Chord length = 2 𝑟2 − 𝑑2
= 2 82 − 62
= 2 64 − 36
= 2 28
= 10.58 cm

32. SEMICIRCLE

33. PERIMETER OF A SEMICIRCLE
 Remember that the perimeter is the distance
round the outside. A semicircle has two edges.
One is half of a circumference and the other is
a diameter
 So, the formula for the perimeter of a semicircle
is:
Perimeter = πr + 2r

34. EXAMPLE (PERIMETER)
Perimeter = πr + 2r
= (3.142)
8
2
+ 8
= 20.56 cm

35. AREA OF A SEMICIRCLE
 A semicircle is just half of a circle. To find the
area of a semicircle we just take half of the
area of a circle.
 So, the formula for the area of a semicircle is:
Area =
1
2
π𝑟2

36. EXAMPLE (AREA)
Area =
1
2
π𝑟2
=
1
2
x 3.142 x 42
= 25.14 cm2

37. SUMMARY

38. THANK YOU !