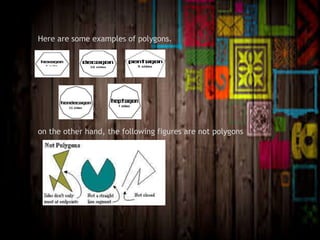
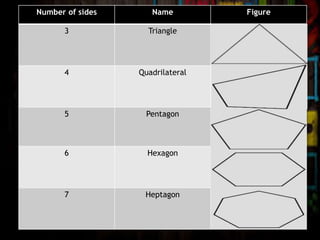
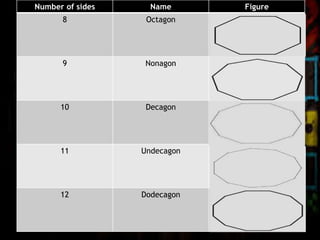
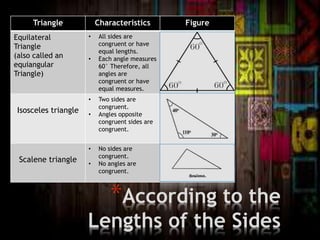
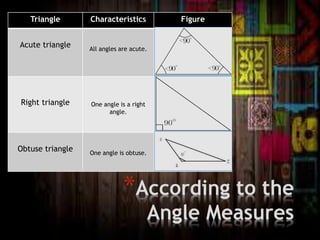
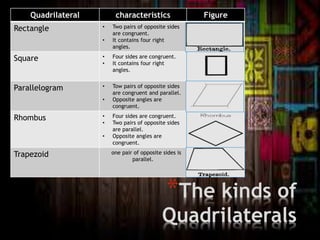
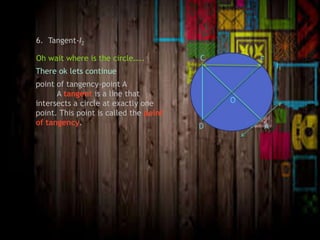
The document discusses the classification of polygons and circles, defining polygons as closed plane figures formed by line segments and highlighting circles as a distinct category due to their lack of such boundaries. It details various types of triangles and quadrilaterals, including their properties and classifications based on sides and angles. Additionally, the document explains the components of a circle, including the center, radius, diameter, chord, secant, and tangent.

1. *Polygons And
Circles
this presentation is written G

2. As your can see here……
There are triangles,
squares,rectangles,circles,
and other plane figures.
These plane figures are
called polygons.
A polygons is a closed
plane figure bounded by
line segments. A circle is
an exception. It is not a
polygon since it is not
bounded by line segments.

3. Here are some examples of polygons.
on the other hand, the following figures are not polygons

4. Number of sides Name Figure
3 Triangle
4 Quadrilateral
5 Pentagon
6 Hexagon
7 Heptagon

5. Number of sides Name Figure
8 Octagon
9 Nonagon
10 Decagon
11 Undecagon
12 Dodecagon

6. * Triangles and
quadrilaterals are further
classified into different
kinds.
Triangles are polygons with three sides, three angles, and
three vertices. The sum of the interior angles of a
triangle is 180°. Triangles are classified in two
ways…

7. *According to the
Lengths of the Sides
Triangle Characteristics Figure
Equilateral
Triangle
(also called an
equiangular
Triangle)
• All sides are
congruent or have
equal lengths.
• Each angle measures
60° Therefore, all
angles are
congruent or have
equal measures.
Isosceles triangle
• Two sides are
congruent.
• Angles opposite
congruent sides are
congruent.
Scalene triangle
• No sides are
congruent.
• No angles are
congruent.

8. *According to the
Angle Measures
Triangle Characteristics Figure
Acute triangle All angles are acute.
Right triangle One angle is a right
angle.
Obtuse triangle One angle is obtuse.

9. * are polygons
with four sides, four
angles, and four vertices.
The sum of the interior
angles of a quadrilateral is
360°
* Quadrilaterals

10. *The kinds of
Quadrilaterals
Quadrilateral characteristics Figure
Rectangle • Two pairs of opposite sides
are congruent.
• It contains four right
angles.
Square • Four sides are congruent.
• It contains four right
angles.
Parallelogram • Tow pairs of opposite sides
are congruent and parallel.
• Opposite angles are
congruent.
Rhombus • Four sides are congruent.
• Two pairs of opposite sides
are parallel.
• Opposite angles are
congruent.
Trapezoid one pair of opposite sides is
parallel.

11. A circle is a set of all points in a plane
equidistant from a fixed point. The
fixed point is called the center and the
fixed distance from the center to a
point on the circle Is the radius. A
circle is named after its center. Recall
that a circle is not a polygon because it
is not bounded by line segments.
Here is the example…..
A
O
C
D
F
I1
In the figure on the previous page, the parts of a circle are illustrated.
1. center-point O
2. Radius(plural:radii)-𝑂𝐶, 𝑂𝐴, 𝑂𝐷, 𝑂𝐹
A radius of a circle is a line segment from any point on the circle to
its center. A radius of a circle measures half its diameter.
3. chord-𝐶𝐹, 𝐶𝐷, 𝐷𝐹, 𝐶𝐴
4. diameter-𝐶𝐴, 𝐷𝐹
A chore passing through the center of a circle is called a
diameter. A diameter of a circle measures twice its radius.
5. secant-I1
A secant is a line that intersects a circle at exactly two points.

12. 6. Tangent-I2
Oh wait where is the circle…..
There ok lets continue
point of tangency-point A
A tangent is a line that
intersects a circle at exactly one
point. This point is called the point
of tangency.

13. By: Marigold So
Thaaaanks…
THE END