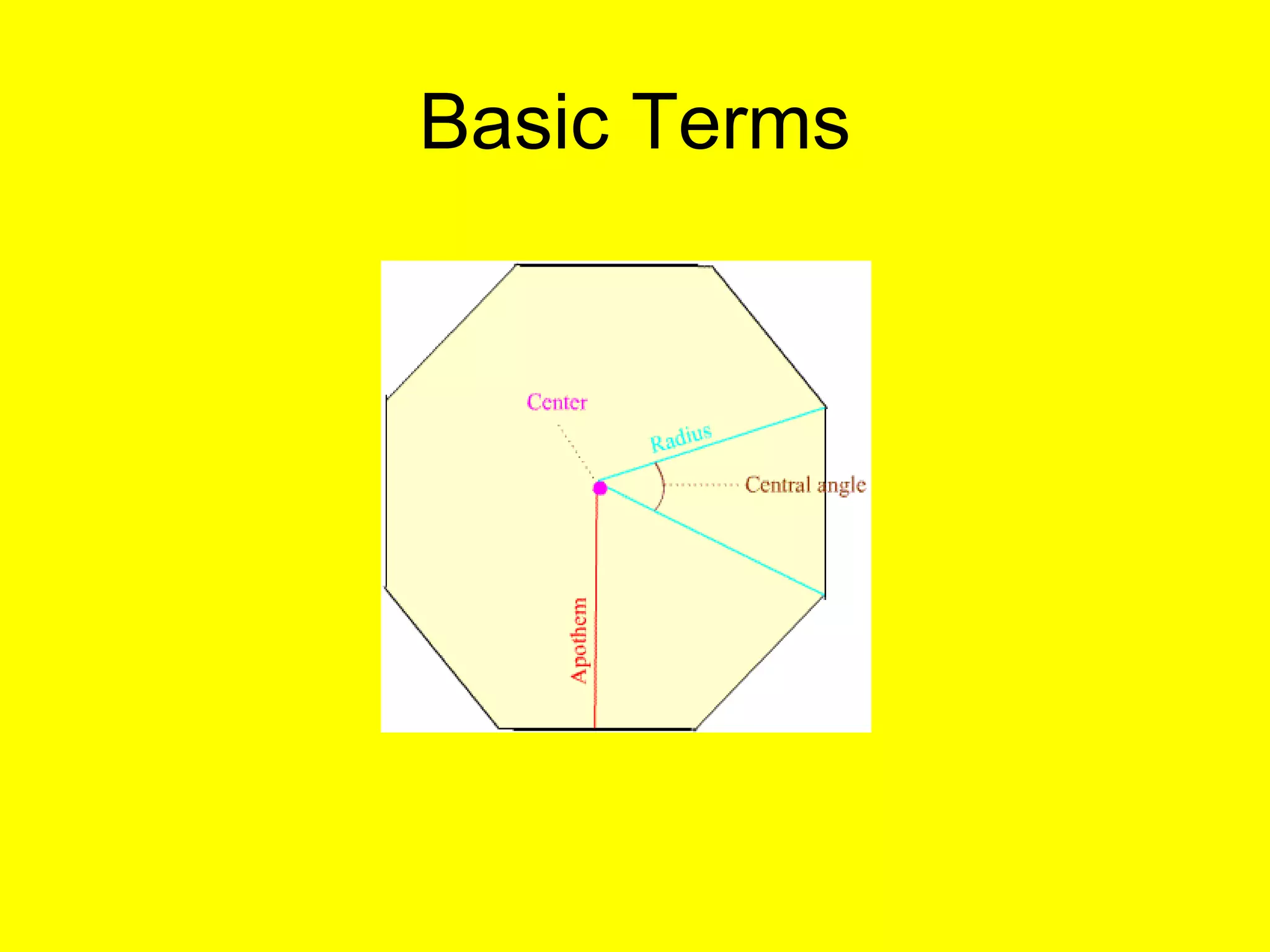
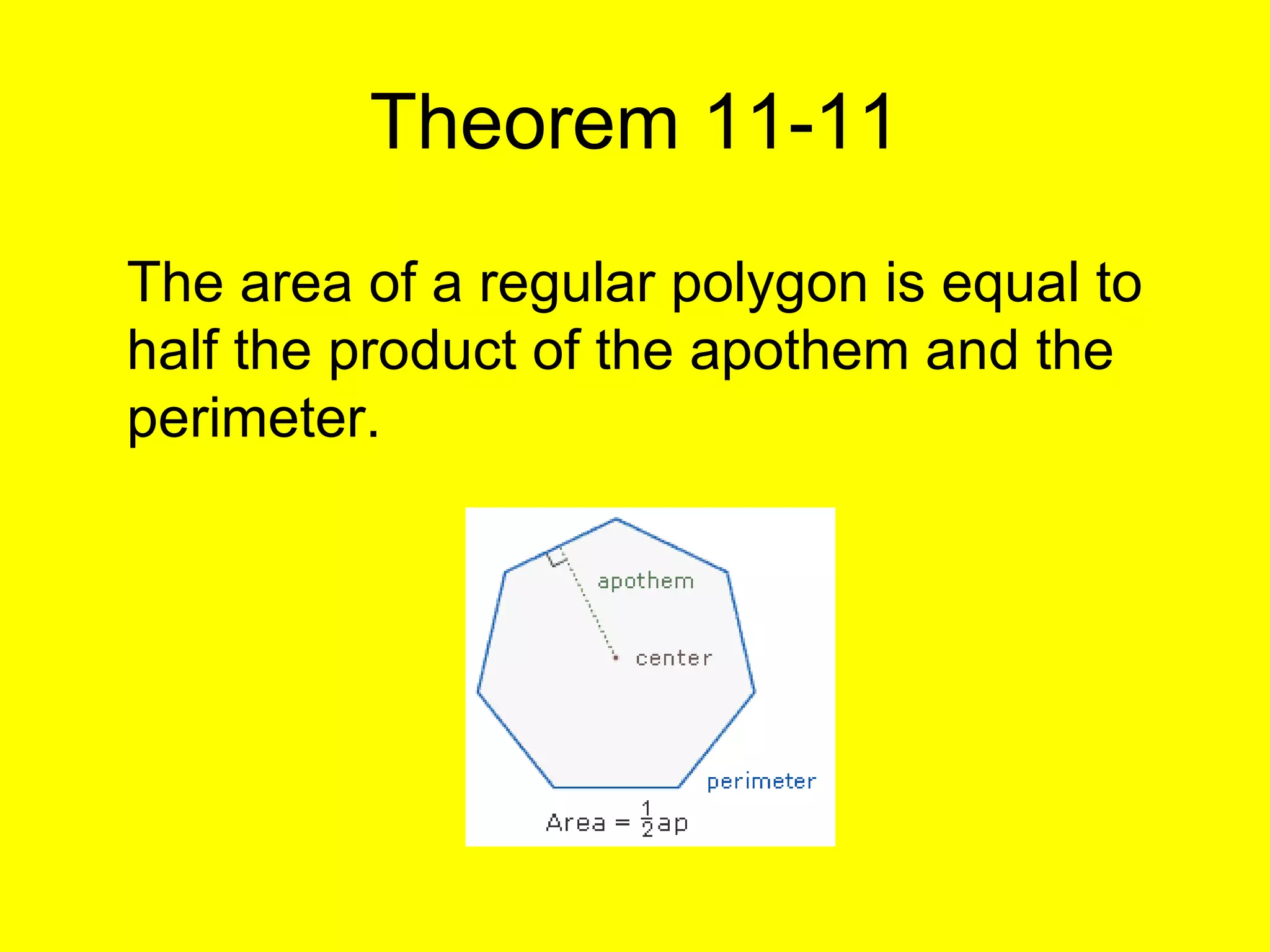
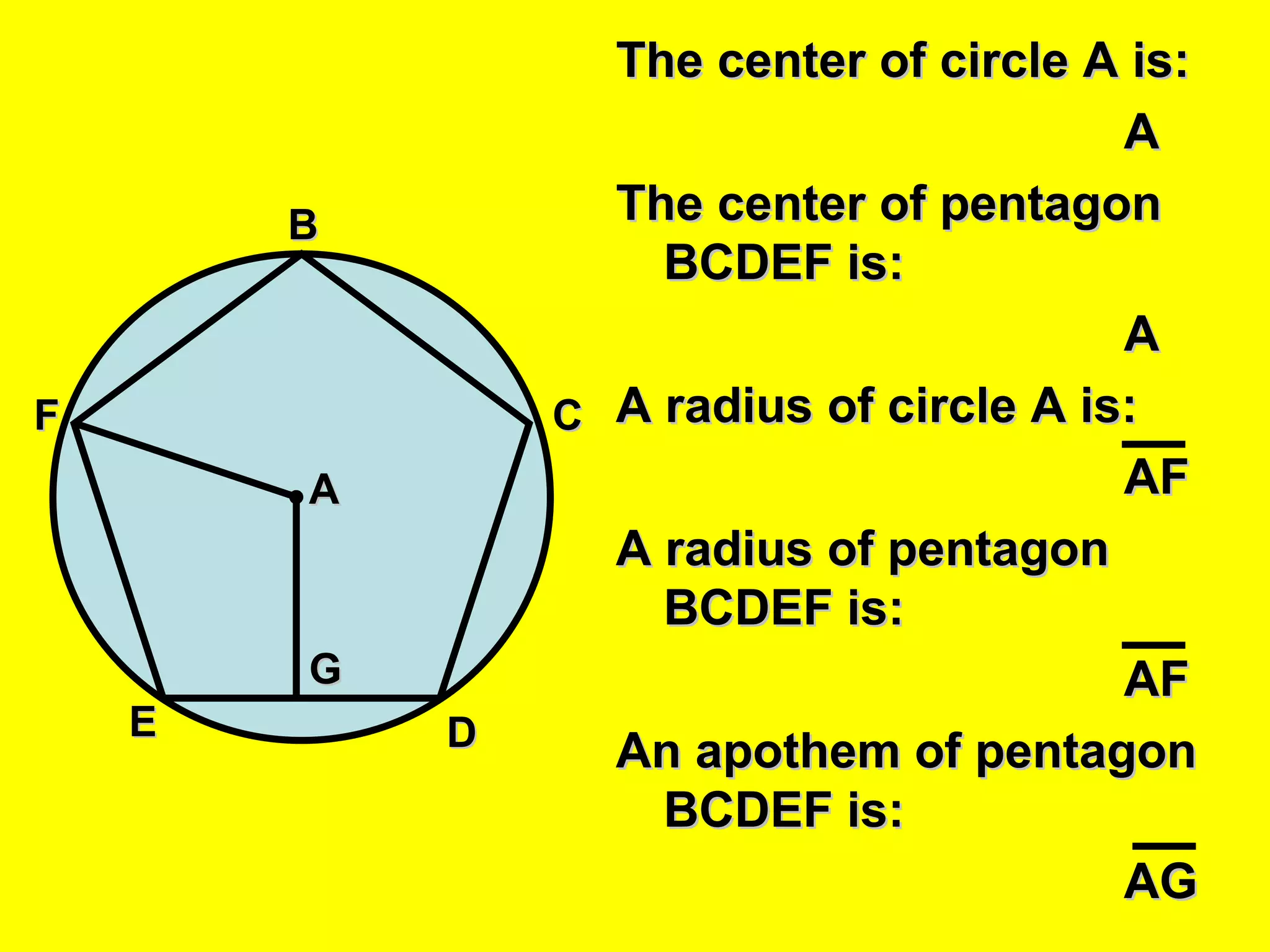
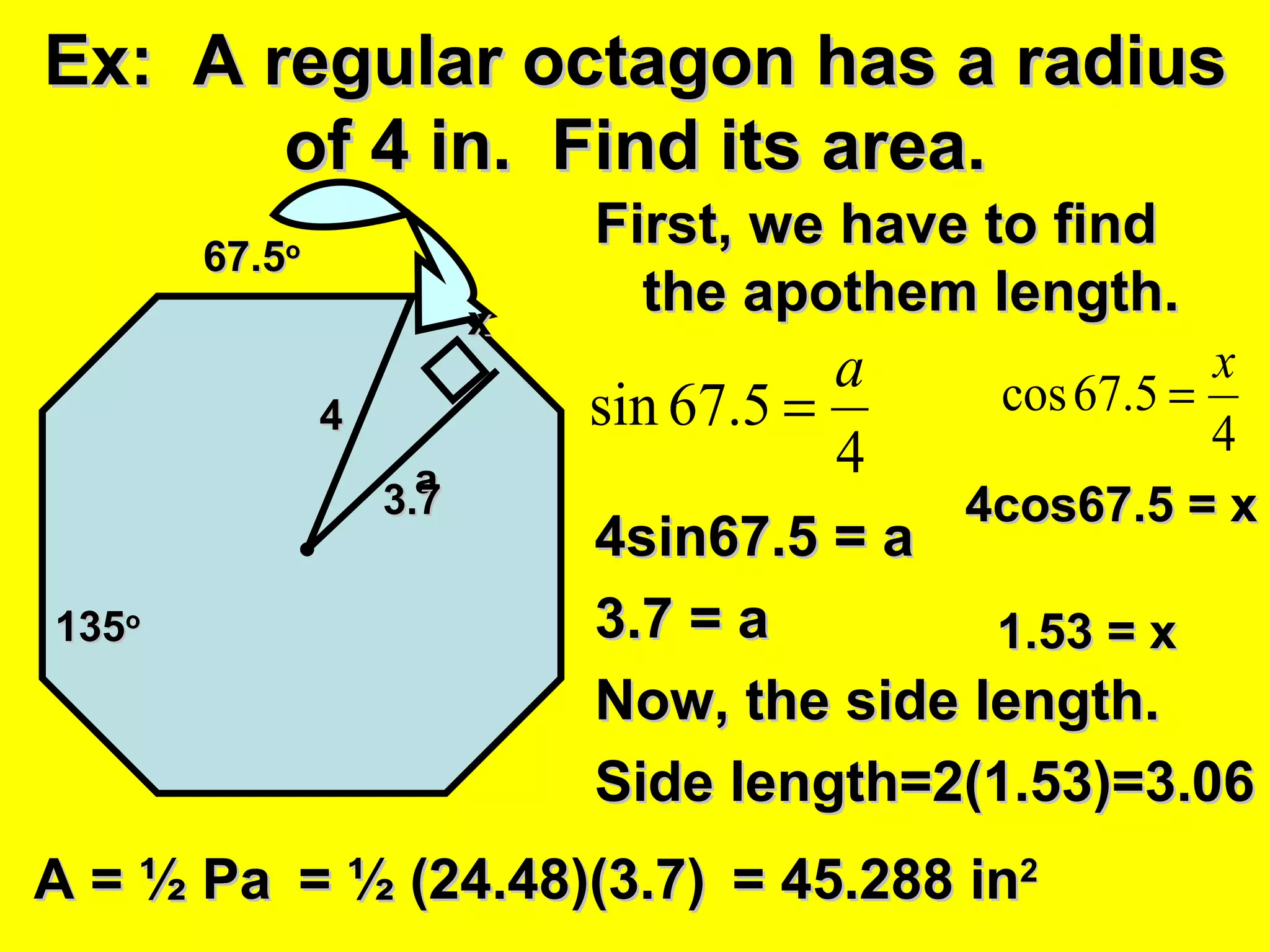
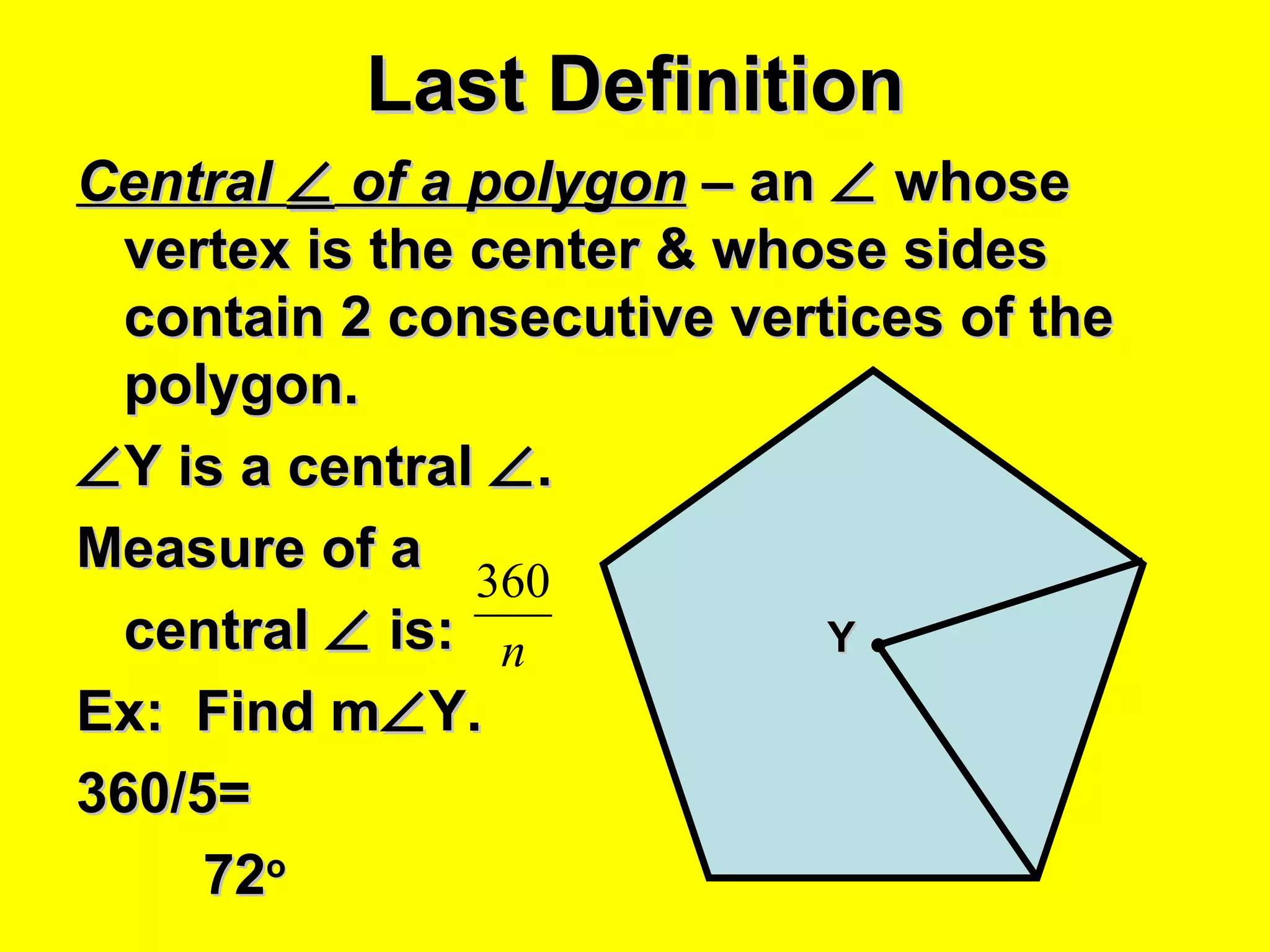
The document discusses the formulas and methods for calculating the area of regular polygons. It defines key terms like the center, radius, apothem, and central angle. It presents the theorem that the area of a regular polygon is equal to half the product of the apothem and perimeter. Examples are given of calculating areas of regular polygons by using the apothem, perimeter, and this area formula. Methods are described for finding the apothem or side length when they are not given.

1. Areas of Regular Polygons Section 11.6

2. Lesson Focus The focus of this lesson is on applying the formula for finding the area of a regular polygon.

3. Basic Terms Center of a Regular Polygon the center of the circumscribed circle Radius of a Regular Polygon the distance from the center to a vertex Central Angle of a Regular Polygon an angle formed by two radii drawn to consecutive vertices Apothem of a Regular Polygon the (perpendicular) distance from the center of a regular polygon to a side

4. Basic Terms

5. Theorem 11-11 The area of a regular polygon is equal to half the product of the apothem and the perimeter.

6. Area of a regular polygon The area of a regular polygon is: A = ½ Pa Area Perimeter apothem

7. The center of circle A is: A The center of pentagon BCDEF is: A A radius of circle A is: AF A radius of pentagon BCDEF is: AF An apothem of pentagon BCDEF is: AG B C D E F A G

8. Area of a Regular Polygon The area of a regular n-gon with side lengths (s) is half the product of the apothem (a) and the perimeter (P), so A = ½ aP, or A = ½ a • ns. NOTE: In a regular polygon, the length of each side is the same. If this length is (s), and there are (n) sides, then the perimeter P of the polygon is n • s, or P = ns The number of congruent triangles formed will be the same as the number of sides of the polygon.

9. More . . . A central angle of a regular polygon is an angle whose vertex is the center and whose sides contain two consecutive vertices of the polygon. You can divide 360 ° by the number of sides to find the measure of each central angle of the polygon. 360/n = central angle

10. Areas of Regular Polygons Center of a regular polygon: center of the circumscribed circle. Radius: distance from the center to a vertex. Apothem: Perpendicular distance from the center to a side. Example 1: Find the measure of each numbered angle. • 1 2 3 360/5 = 72 ½ (72) = 36 L 2 = 36 L 3 = 54 L 1 = 72 Example 2: Find the area of a regular decagon with a 12.3 in apothem and 8 in sides. Area of a regular polygon: A = ½ a p where a is the apothem and p is the perimeter. Perimeter: 80 in A = ½ • 12.3 • 80 A = 492 in 2 Example 3: Find the area. 10 mm • A = ½ a p p = 60 mm 5 mm LL = √3 • 5 = 8.66 a A = ½ • 8.66 • 60 A = 259.8 mm 2

11. But what if we are not given any angles.

12. Ex: A regular octagon has a radius of 4 in. Find its area. First, we have to find the apothem length. 4sin67.5 = a 3.7 = a Now, the side length. Side length=2(1.53)=3.06 4 a 135 o 67.5 o 3.7 x 4cos67.5 = x 1.53 = x A = ½ Pa = ½ (24.48)(3.7) = 45.288 in 2

13. Last Definition Central  of a polygon – an  whose vertex is the center & whose sides contain 2 consecutive vertices of the polygon.  Y is a central  . Measure of a central  is: Ex: Find m  Y. 360/5= 72 o Y

14. Check out! http://www.mathopenref.com/polygonregulararea.html