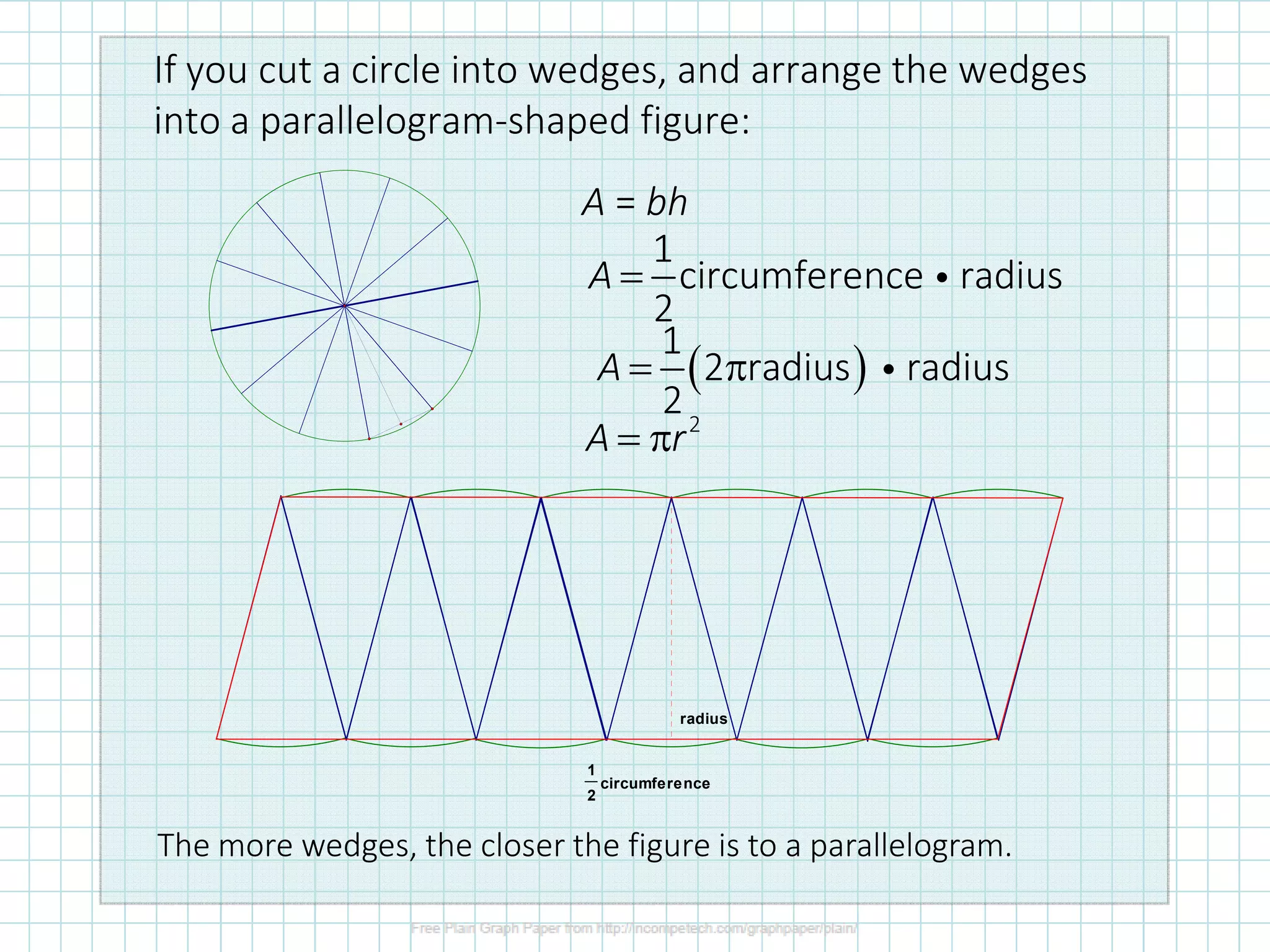
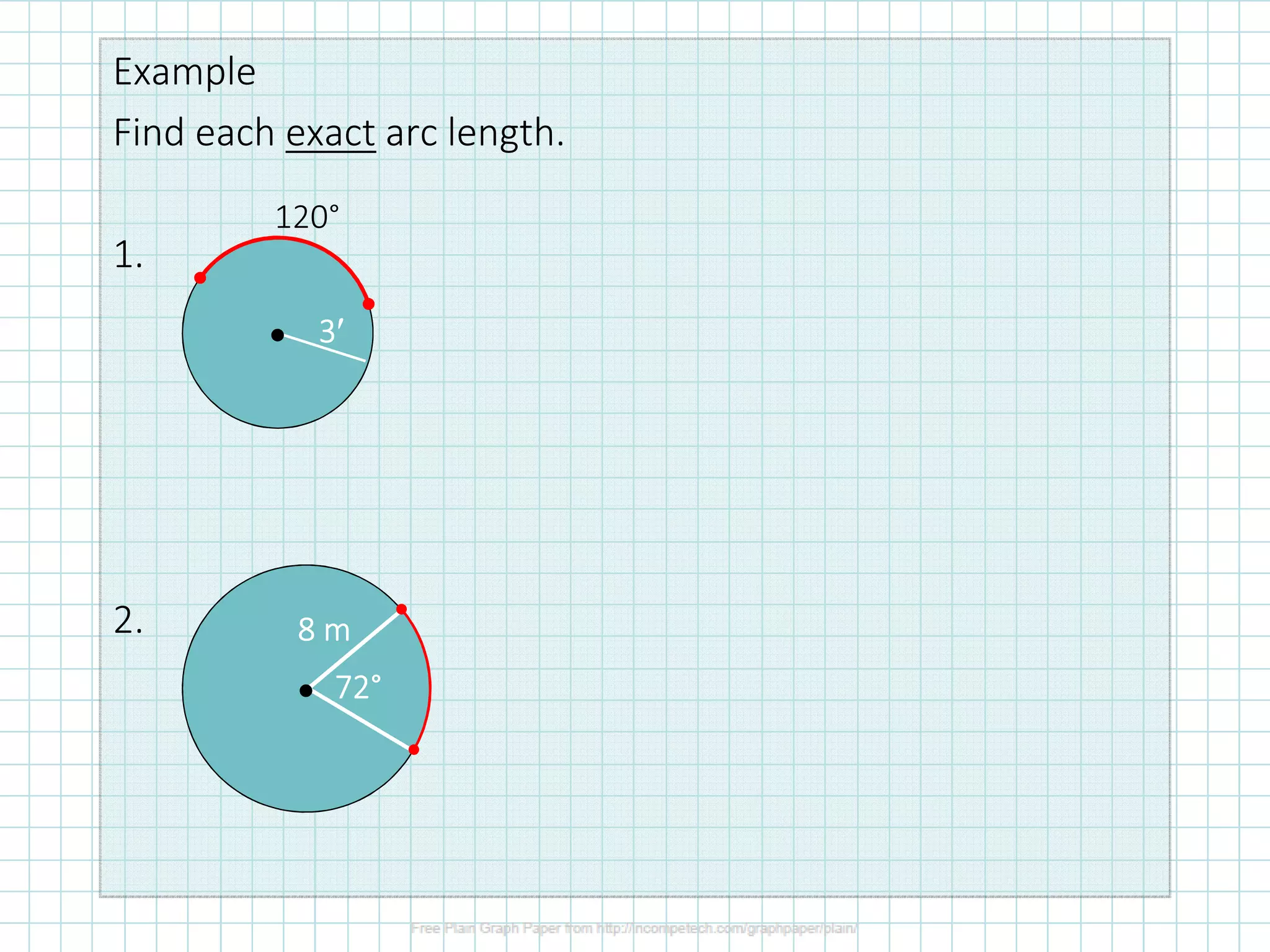
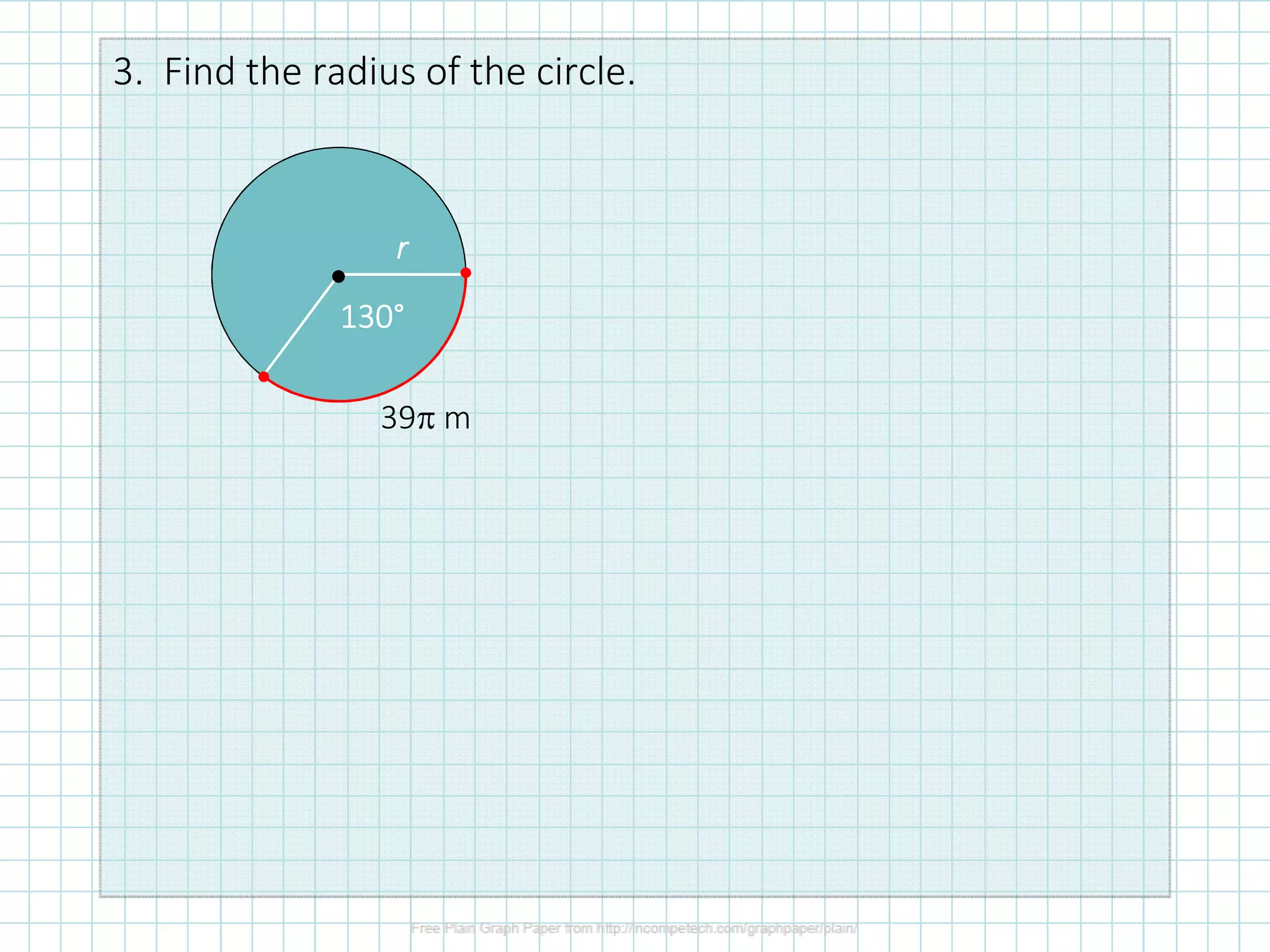
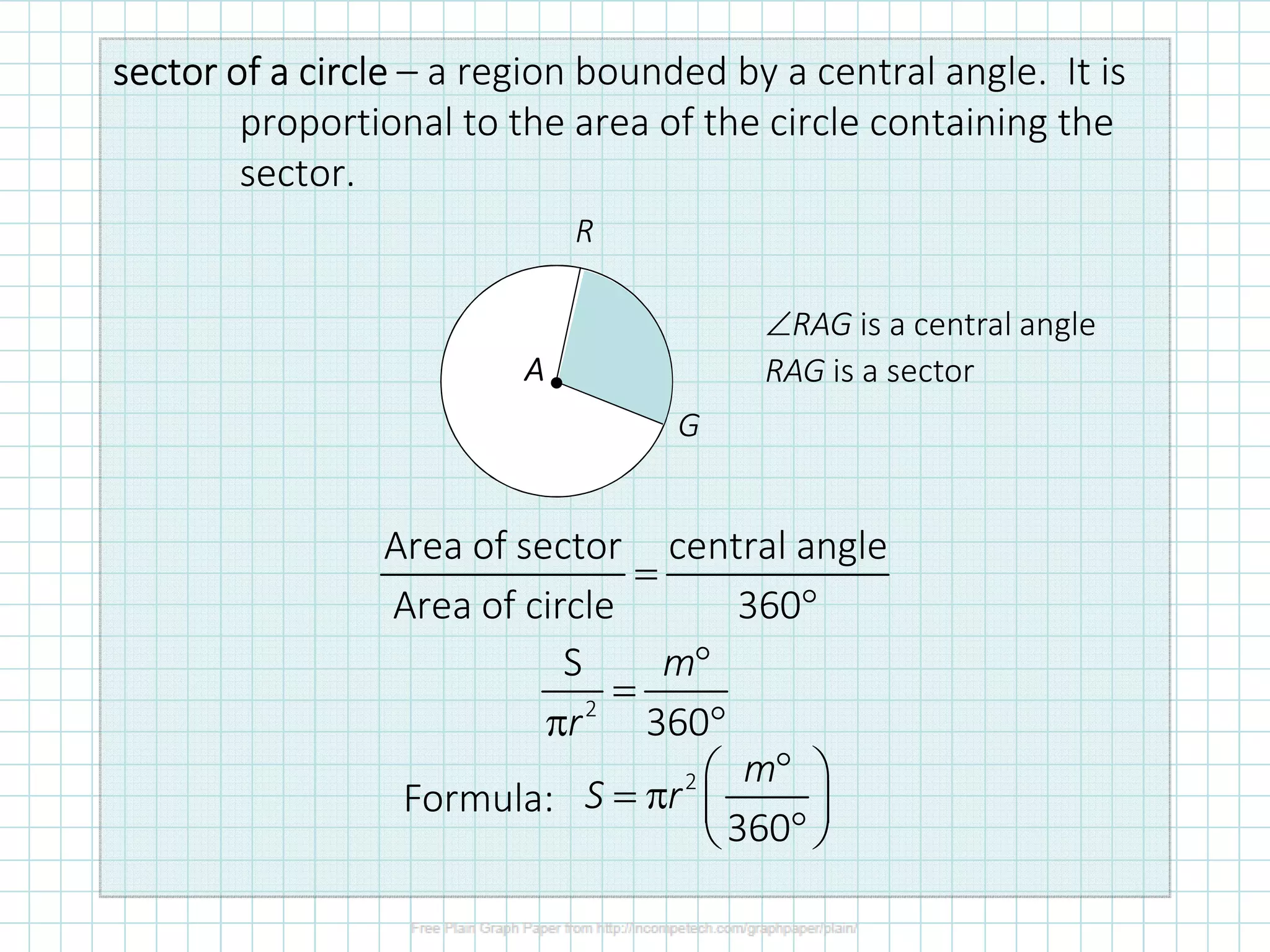
The document discusses formulas for calculating properties of circles such as circumference, area, arc length, and sector area. It defines pi (π) and shows formulas for calculating the circumference and area of a circle using its diameter or radius. Examples are provided for calculating the circumference, diameter, area, radius, arc length, and sector area of various circles.

1. Circumference and Area of Circles
The student is able to (I can):
• Develop and use formulas to find the circumference and
area of circles
• Develop and use formulas to find arc length and sector
area of circles

2. ππππ ((((pi)pi)pi)pi) – the ratio of the circumference to the diameter.
Since the diameter is twice the radius, this formula can also
be written as:
π is an irrational number – it never repeats and it
never ends. The symbol π is an exact number;
3.1415926… is an approximation.
C
d
π =
C d= π
2C r= π
which becomes

3. If you cut a circle into wedges, and arrange the wedges
into a parallelogram-shaped figure:
radius
1
2
circumference
A = bh
1
circumference radius
2
A = i
( )
1
2 radius radius
2
A = π i
2
A r= π
The more wedges, the closer the figure is to a parallelogram.

5. Examples
1. Find the exact circumference and area of a circle whose
diameter is 18 m.
2. Find the diameter and area of a circle whose
circumference is 22π ft.
3. Find the radius of a circle whose area is 81π cm2.

6. Examples
1. Find the exact circumference and area of a circle whose
diameter is 18 m.
C = πd = π(18) = 18π m
A = πr2 = π(92) = 81π m2
2. Find the diameter and area of a circle whose
circumference is 22π ft.
22π = πd
d = 22 ft
A = π(112) = 121π ft2
3. Find the radius of a circle whose area is 81π cm2.
81π = πr2
81 = r2
81 9 cmr = =

7. arcarcarcarc lengthlengthlengthlength – the distance along an arc. It is proportional to
the circumference of the circle.
or
360
m
L C
° 
=  
° 
where C is the circumference
(either C=πd or C=2πr).
•
mmmm°°°°
m° arc length central angle
circumference 360
360
L m
C
=
°
°
=
°

8. Example
Find each exact arc length.
1.
2.
120°
• 3333′′′′
72727272°°°°
8 m8 m8 m8 m
•

9. Example
Find each exact arc length.
1.
2.
120°
• 3333′′′′
( )
120
2 3
360
2 ft.
L
 
= π  
 
= π
( )
72
2 8
360
16
or 3.2 m
5
L
 
= π  
 
= π π
72727272°°°°
8 m8 m8 m8 m
•

10. 3. Find the radius of the circle.
•
130130130130°°°°
rrrr
39π m

11. 3. Find the radius of the circle.
•
130130130130°°°°
rrrr
39π m
39 130
2 360
260 14040
14040
54 m
260
r
r
r
π °
=
π °
π = π
π
= =
π

12. sector of asector of asector of asector of a circlecirclecirclecircle – a region bounded by a central angle. It is
proportional to the area of the circle containing the
sector.
•
R
AAAA
G
∠RAG is a central angle
RAG is a sector
Area of sector central angle
Area of circle 360
=
°
2
S
360
m
r
°
=
π °
2
360
m
S r
° 
= π  
° 
Formula:

13. Examples
Find the area of each sector. Leave answers in terms of π.
1.
2.
•
120° 2"2"2"2"
• 72°
10m10m10m10m

14. Examples
Find the area of each sector. Leave answers in terms of π.
1.
2.
•
120° 2"2"2"2"
• 72°
10m10m10m10m
( )2
2
120
2
360
4 120 480
360 360
4
in
3
S
°
= π
°
π⋅ π
= =
= π
( )2
2
72
10
360
7200
20 m
360
S
° 
= π  
° 
π
= = π