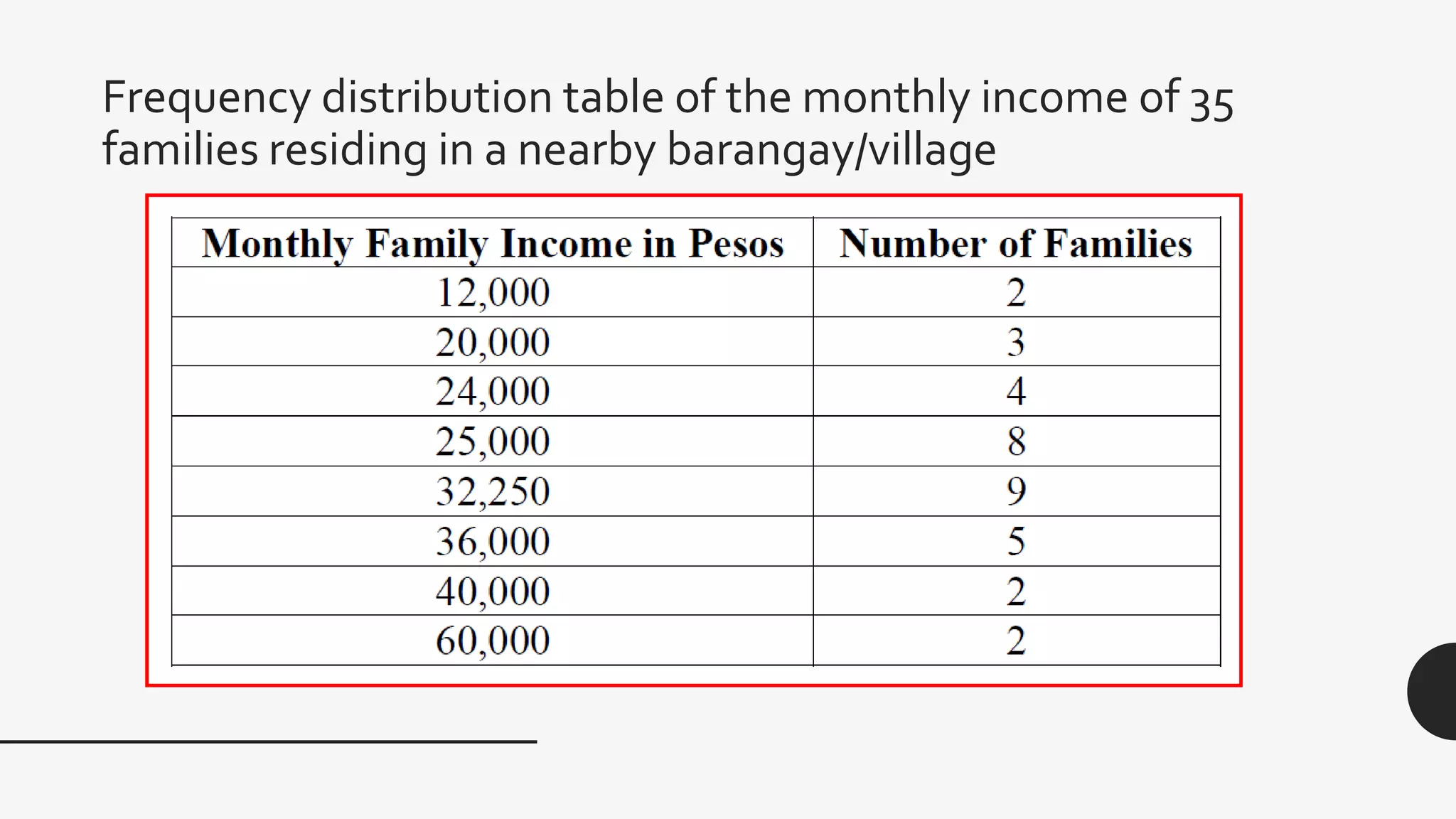
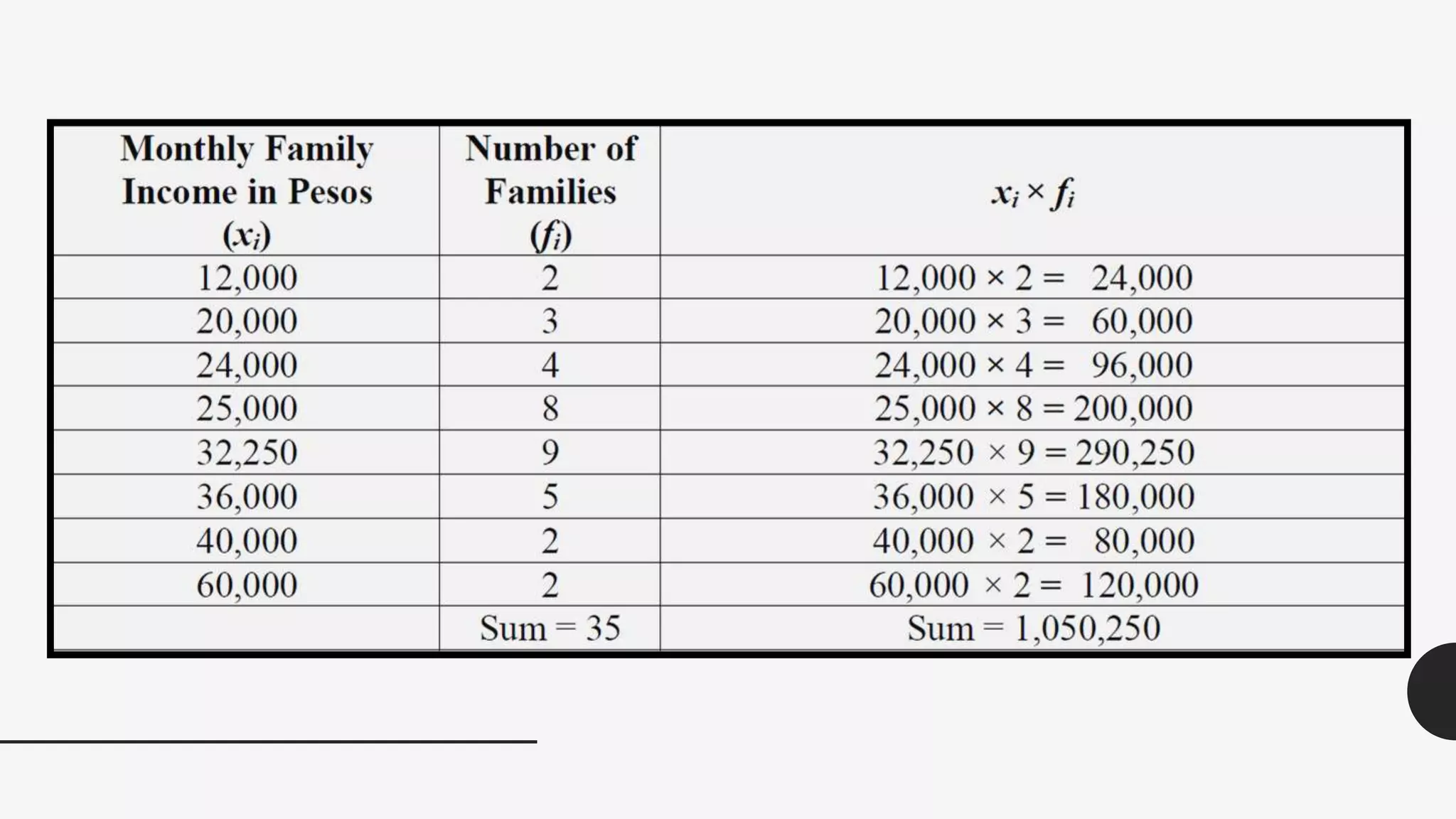
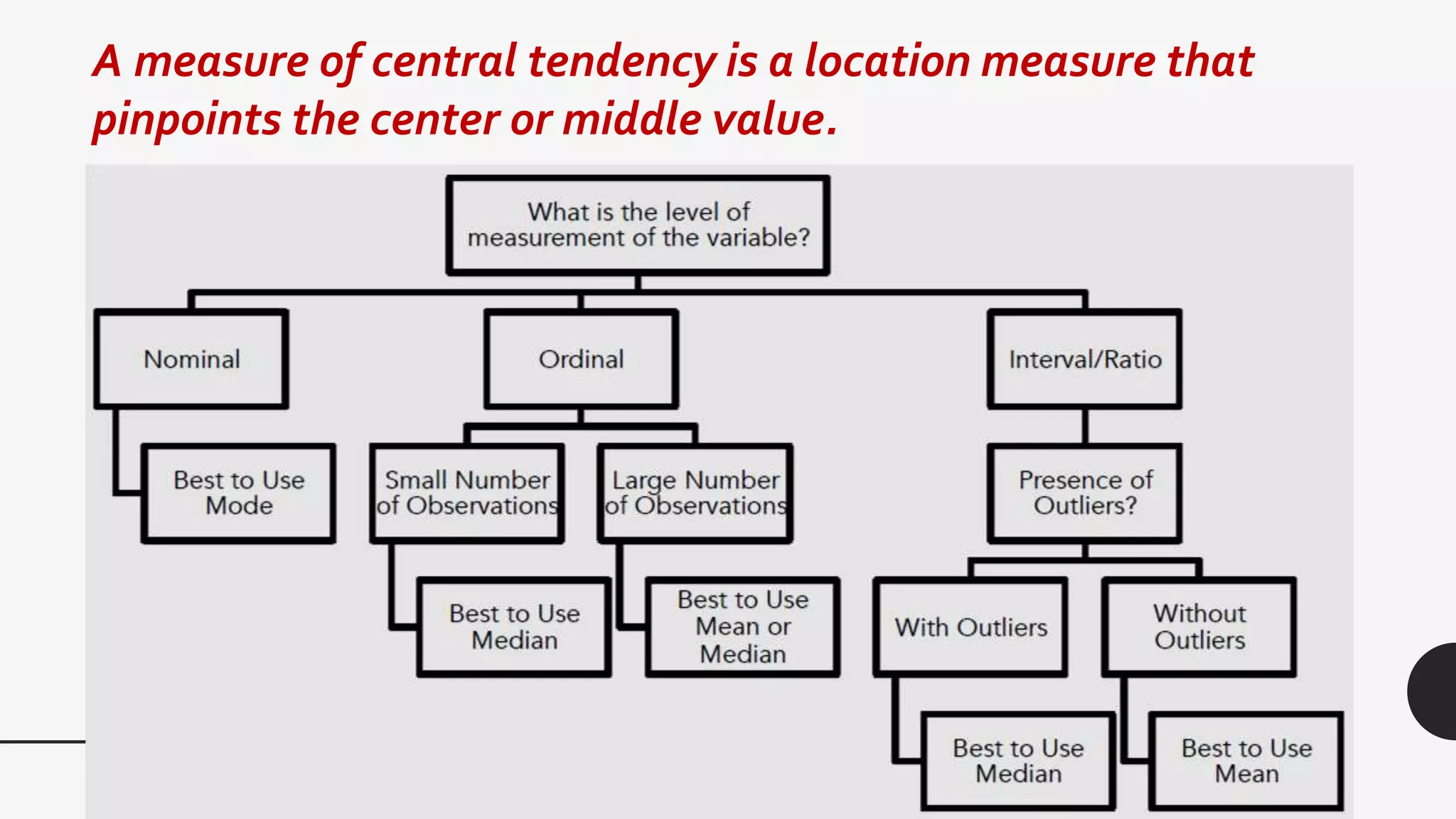
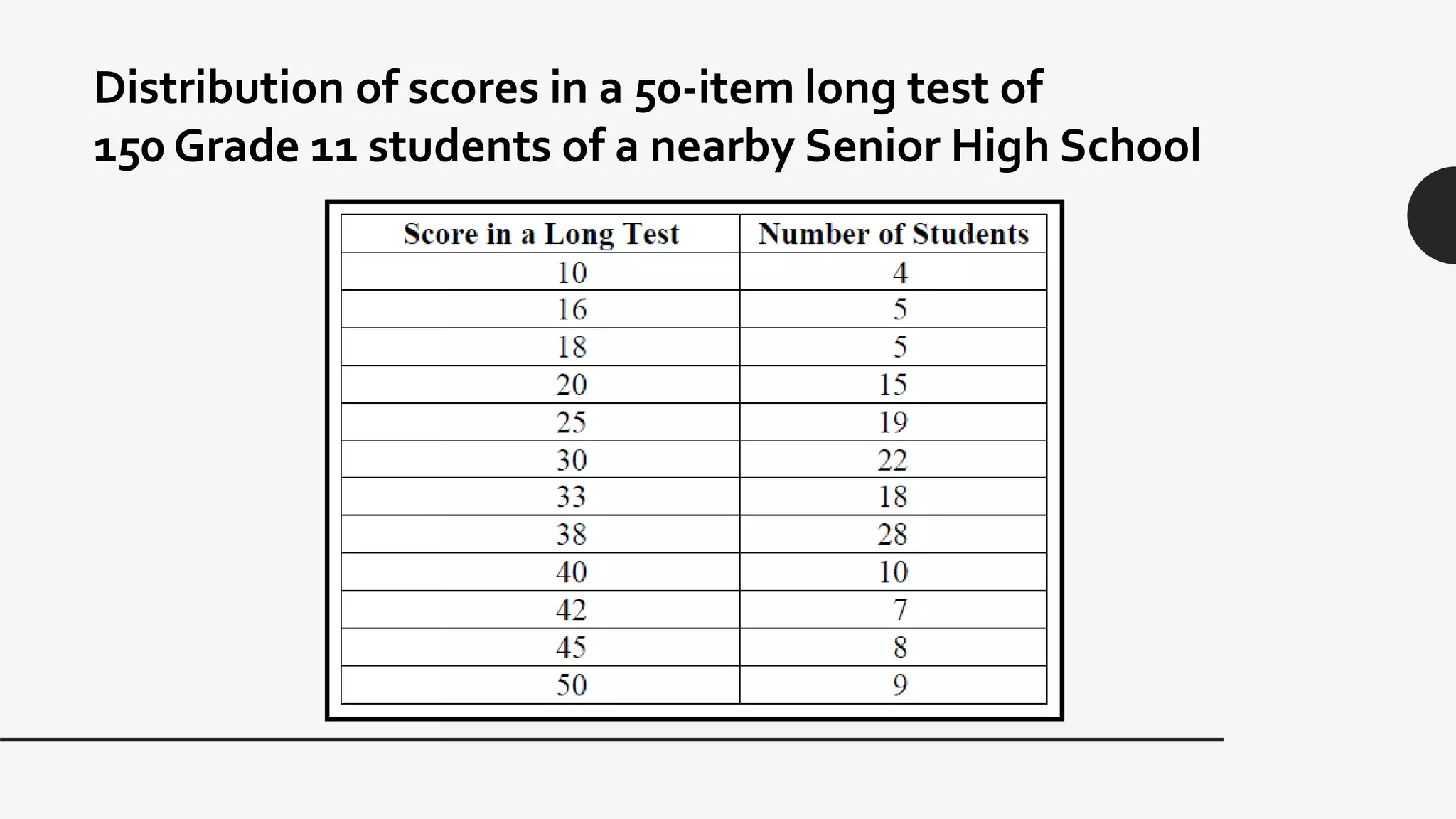
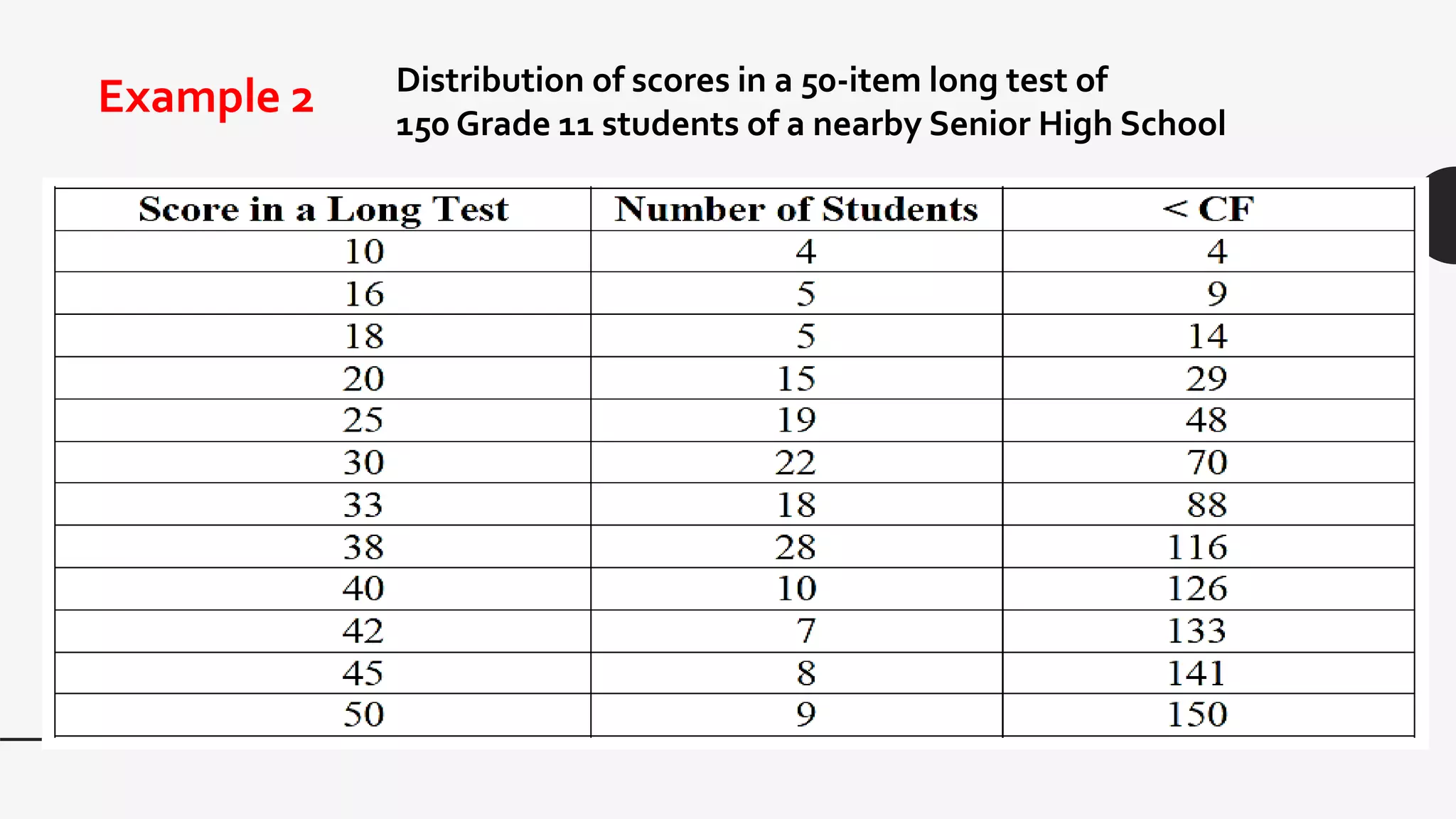
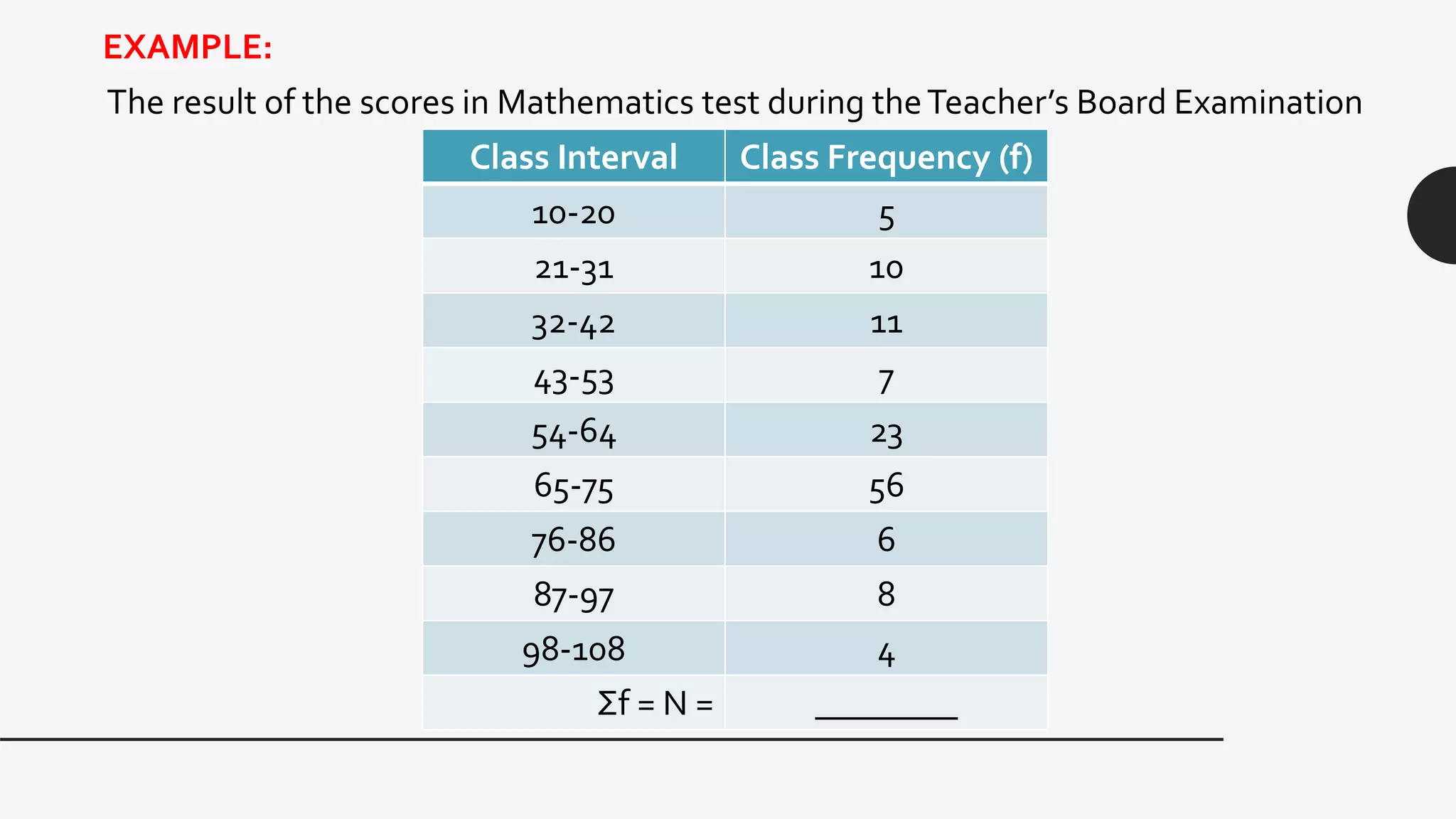
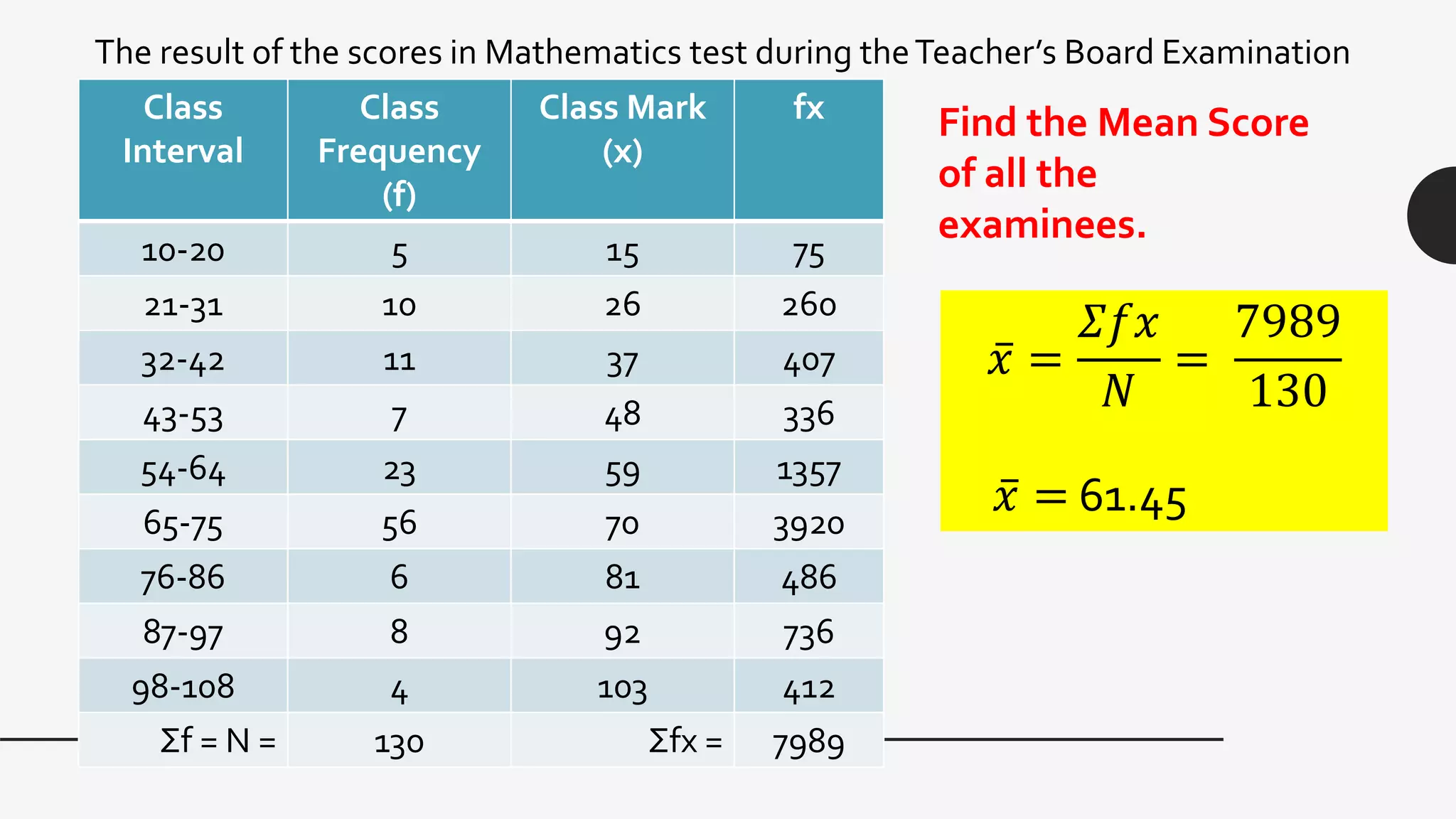
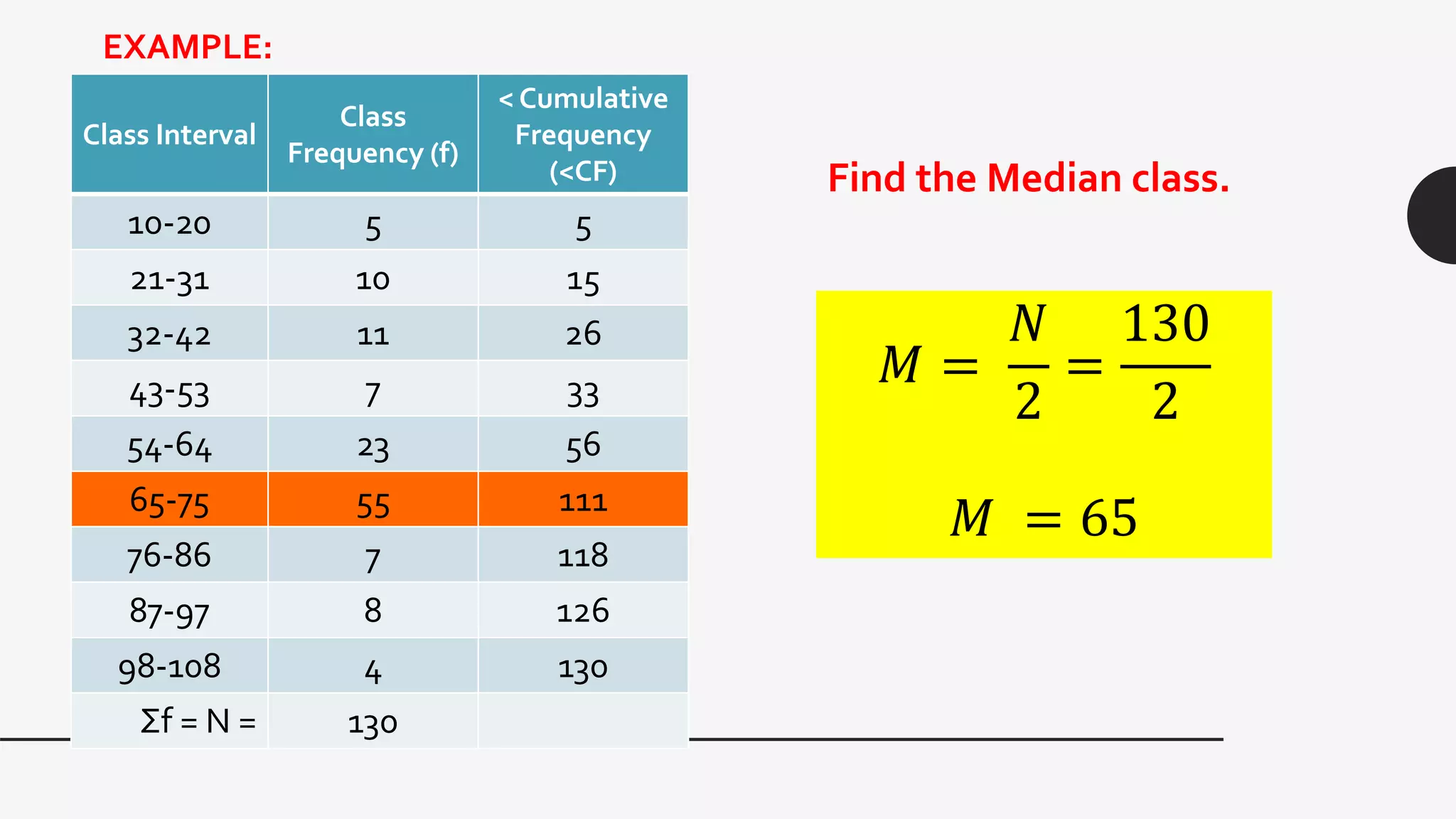
This document provides examples and explanations of key measures of central tendency (mean, median, mode) and location (percentiles, deciles, quartiles) using data from test scores. It discusses how to calculate each measure and their properties. For a grouped data set of 130 test scores ranging from 10-108, it demonstrates calculating the mean as 61.45 and identifies the median class as 54-64 since it contains the value of 65, which is the midpoint of the data set. The document provides guidance on finding percentiles, deciles, and quartiles using the percentile formula and examples.

1. STATISTICS AND
PROBABILITY
Lesson 6 and Lesson 7
Ms. Maria Christita Polinag
Miriam College Adult Education

2. MEASURES OF
CENTRAL
TENDENCY
LESSON 6

3. Frequency distribution table of the monthly income of 35
families residing in a nearby barangay/village

4. 1. What is the highest monthly family income? Lowest?
2.What monthly family income is most frequent in the village?
3. If you list down individually the values of the monthly family
income from lowest to highest, what is the monthly family
income where half of the total number of families have monthly
family income less than or equal to that value while the other
half have monthly family income greater than that value?
4.What is the average monthly family income?

5. 1. What is the highest monthly family income? Lowest?
Maximum and Minimum
- summary measures of a data set
- these measures do not give
a measure of location in the center of the distribution
Answer: Highest monthly family income is 60,000 pesos
while the lowest is 12,000 pesos.

6. 2. What monthly family income is most frequent in the village?
ModalValue or Mode
-the value with the highest frequency
-is the most fashionable value in the data set
Answer: Monthly family income that is most frequent is
32,250 pesos.

7. 3. If you list down individually the values of the monthly
family income from lowest to highest, what is the monthly
family income where half of the total number of families
have monthly family income less than or equal to that value
while the other half have monthly family income greater
than that value?

8. Median
32, 250
When arranged in increasing order or the data come in
an array as in the following:
12,000; 12,000; 20,000; 20,000; 20,000; 24,000; 24,000;
24,000; 24,000; 25,000; 25,000;25,000; 25,000; 25,000;
25,000; 25,000; 25,000; 32,250; 32,250; 32,250; 32,250;
32,250; 32,250; 32,250; 32,250; 32,250; 36,000; 36,000;
36,000; 36,000; 36,000; 40,000; 40,000; 60,000; 60,000;

9. Median
- is found in the center of the distribution.
If N is odd the Median is the observation in the
array
If N is even the Median is the average of the two middle
values or it is average of the and
observation s

10. 4. What is the average monthly family income?
Arithmetic Mean or Mean
-is computed by adding all the values and then the sum
is divided by the number of values included in the sum
- is also found somewhere in the center of the
distribution
Answer: When computed using the data values, the average
is 30,007.14 pesos.

11. Summation: ‘sum of observations represented by xi
where i takes the values from1 to N,
and N refers to the total number of
observations being added’
Arithmetic Mean or Mean

12. Using the example with 35 observations of family
income, the mean is computed as:
Mean :
μ = 30, 007.14

14. PROPERTIES OFTHE MEAN, MEDIAN AND MODE
 basis for determining what measure to use to represent
the center of the distribution
Arithmetic Mean or Mean
 computed only for quantitative variables that are
measured at least in the interval scale
 linked to a “center of gravity”

15.  each observation has a contribution to the
value of the mean

16.  are also amenable to further computation; you
can combine subgroup means to come up with
the mean for all observations
Arithmetic Mean or Mean
Example:
If there are 3 groups with means equal to 10, 5 and 7
computed from 5, 15, and 10 observations respectively.

17. Arithmetic Mean or Mean
 outliers do affect the value of the mean
-If there are extreme large values, the mean will tend to
be ‘pulled upward’
-if there are extreme small values, the mean will tend to
be ‘pulled downward’
 In the presence of extreme values or outliers, the mean is not
a good measure of the center

18. Median
 computed for quantitative variables
 but can be computed for variables measured in at
least in the ordinal scale, in determining the center of
the distribution
 it is not easily affected by extreme values or outliers

19. ModalValue or Mode
 computed for the data set which are mainly measured in the
nominal scale of measurement; sometimes referred to as the
nominal average
 can easily be picked out by ocular inspection, especially if the
data are not too many
 more helpful measure for discrete and qualitative data with
numeric codes than for other types of data

20. ModalValue or Mode
o unimodal if there is a unique mode
o bimodal if there are two modes
o multimodal if there are more than two modes

21. A measure of central tendency is a location measure that
pinpoints the center or middle value.

22. OTHER
MEASURES OF
LOCATION
LESSON 7

23. Distribution of scores in a 50-item long test of
150 Grade 11 students of a nearby Senior High School

24. 1. What is the highest score? Lowest score?
2.What is the most frequent score?
3.What is the median score?
4.What is the average or mean score?

25. 1.What is the highest score? Lowest score?
Answer: Highest score is 50 while the lowest is 10.
2.What is the most frequent score?
Answer: Most frequent score is 38 which is the score of 28
students.
3.What is the median score?
Answer: The median score is 33 which implies that 50% of the
students or around 75 students have score at most 33.
4.What is the average or mean score?
Answer: On the average, the students got 32.04667 or 32
(rounded off) out of 50 items correctly.

26. 1. What is the score where at most 75% of the 150
students scored less or equal to it?
2. Do you think the long test is easy since 75 students
have scores at most 33 out of 50?
3. Do you need to be alarmed when 10% of the class got a
score of at most 20 out of 50?
Questions could be answered by knowing other
measures of location:

27. Measures of Location: Maximum, Minimum, Percentiles,
Deciles and Quatiles
Percentile is a measure that pinpoints a location that
divides distribution into 100 equal parts.
It is usually represented by Pj, that value which
separates the bottom j% of the distribution from the
top (100-j)%.

28.  It is usually represented by Pj, that value which separates the
bottom j% of the distribution from the top (100-j)%.
- P30 is the value that separates the bottom 30% of the
distribution to the top 70%
- we say 30% of the total number of observations in the data
set are said to be less than or equal to P30 while the remaining
70% have values greater than P30.

29. Step 1: Arrange the data values in ascending order of
magnitude.
Step 2: Find the location of Pj in the arranged list by
computing L = (j/100) x N, where N is the total number of
observations in the data set.
Step 3:
a. If L is a whole number, then Pj is the mean or average of
the values in the Lth and (L+1)th positions.
b. If L is not a whole number, then Pj is the value of the next
higher position.
Steps in finding the jth percentile (Pj)

30. Example 2 Distribution of scores in a 50-item long test of
150 Grade 11 students of a nearby Senior High School

31. Step 1: Arrange the data values in ascending order of
magnitude.
To find P30 we note that j = 30
Distribution of scores in a 50-item long test of
150 Grade 11 students of a nearby Senior High SchoolExample 2
Step 2: Find the location of Pj in the arranged list by
computing L = (j/100) x N, where N is the total number of
observations in the data set.

32. Step 3:
a. If L is a whole number, then Pj is the mean or average of the values
in the Lth and (L+1)th positions.
b. If L is not a whole number, then Pj is the value of the next higher
position.
Distribution of scores in a 50-item long test of
150 Grade 11 students of a nearby Senior High School
Example 2
 45 is a whole number and thus we follow the first rule
 the average or mean of the values found in the 45th and 46th
positions, which are both 25
 the bottom 30% of the scores are said to be less than or
equal to 25
 while the top 70% of the observations (which is around 105)
are greater than 25

33. Example 2 Distribution of scores in a 50-item long test of
150 Grade 11 students of a nearby Senior High School

34. Deciles
divide the distribution into 10 equal parts
Quartiles
divide the distribution into 4 equal parts
Deciles and Quartiles

35. HOW DOWE USETHE
PERCENTILE IN
FINDINGTHE DECILES
AND QUARTILES OF A
DISTRIBUTION?

36.  Compute for the 3rd Decile or D3
 Compute for the 3rd Quartile or Q3
Using the steps in finding the Percentile:

37.  Compute for the 3rd Decile or D3
D3 = P30
 Compute for the 3rd Quartile or Q3
Q3 = P75
Using the steps in finding the Percentile:

38. MEAN, MEDIAN &
MODE (FOR
GROUPED DATA)

39. MEAN for Grouped Data:
Class
Interval
Class
Frequency (f)
Class Mark
(x)
fx
𝑥 =
𝑓1 𝑥1 + 𝑓2 𝑥2 + 𝑓3 𝑥3 + ⋯ 𝑓𝑛−1 𝑥 𝑛−1 + 𝑓𝑛 𝑥 𝑛
𝑁
=
𝛴𝑓𝑥
𝑁

40. EXAMPLE:
Class Interval Class Frequency (f)
10-20 5
21-31 10
32-42 11
43-53 7
54-64 23
65-75 56
76-86 6
87-97 8
98-108 4
Σf = N = ________
The result of the scores in Mathematics test during theTeacher’s Board Examination

41. Find the Mean Score
of all the
examinees.
Class
Interval
Class
Frequency
(f)
Class Mark
(x)
fx
10-20 5 15 75
21-31 10 26 260
32-42 11 37 407
43-53 7 48 336
54-64 23 59 1357
65-75 56 70 3920
76-86 6 81 486
87-97 8 92 736
98-108 4 103 412
Σf = N = 130 Σfx = 7989
The result of the scores in Mathematics test during theTeacher’s Board Examination
𝑥 =
𝛴𝑓𝑥
𝑁
=
7989
130
𝑥 = 61.45

42. MEDIAN for grouped Data:
Class Interval
Class Frequency
(f)
< Cumulative
Frequency (<CF)
𝑀 =
𝑁
2
Median Class is the class interval to which
M is included with respect to the less than
cumulative frequency.
𝑥 = 𝑥 𝐿𝐵 + 𝑖
𝑁
2
− < 𝑐𝑓𝑏
𝑓𝑚

43. EXAMPLE:
Class Interval
Class
Frequency (f)
< Cumulative
Frequency
(<CF)
10-20 5 5
21-31 10 15
32-42 11 26
43-53 7 33
54-64 23 56
65-75 55 111
76-86 7 118
87-97 8 126
98-108 4 130
Σf = N = 130
Find the Median class.
𝑀 =
𝑁
2
=
130
2
𝑀 = 65

44. Class Interval
Class
Frequency (f)
< Cumulative
Frequency
(<CF)
43-53 7 33
54-64 23 56
65-75 55 111
76-86 7 118
Find the Median for the grouped data
𝑥 = 𝑥 𝐿𝐵 + 𝑖
𝑁
2
− < 𝑐𝑓𝑏
𝑓𝑚
1. Lower class boundary of M
𝑥 𝐿𝐵 = 𝐿𝐿 − 0.5
𝑥 𝐿𝐵= 65 − 0.5 = 64.5
2. Class size (i)
𝑖 = 𝑈𝐿 − 𝐿𝐿 + 1
𝑖 = 75 − 65 + 1 = 11

45. Class
Interval
Class
Frequency (f)
< Cumulative
Frequency
(<CF)
43-53 7 33
54-64 23 56
65-75 55 111
76-86 7 118
Find the Median for the grouped data
𝑥 = 𝑥 𝐿𝐵 + 𝑖
𝑁
2
− < 𝑐𝑓𝑏
𝑓𝑚
= 64.5 + 11
130
2
− 56
55
𝑥 = 64.5 + 11
65 − 56
55
= 64.5 + 11
9
55
= 64.5 + 11 0.16363
𝑥 = 64.5 + 1.8 = 66.3
3. Less than cumulative frequency
before the median class
< 𝑐𝑓𝑏 = 56
4. Median class frequency
𝑓𝑚 = 55

46. MODE for grouped Data:
Class Interval Class Frequency (f)
Modal Class is the class interval with the
heights class frequency.
𝑥 = 𝑥 𝐿𝐵 + 𝑖
𝑓𝑚 − 𝑓𝑚𝑏
2𝑓𝑚 − 𝑓𝑚𝑎 − 𝑓𝑚𝑏

47. Find the Mode for the grouped data.
Class
Interval
Class
Frequency (f)
43-53 7
54-64 23
65-75 55
76-86 7
𝑥 𝐿𝐵 = 65 − 0.5 = 64.5
1. Lower class boundary of the modal class
2. Class size 𝑖 = 75 − 65 + 1 = 11
3. Class frequency of the modal class 𝑓𝑚 = 55
4. Class frequency of the class after the modal class
𝑓𝑚𝑎 = 7
5. Class frequency of the class before the modal class
𝑓𝑚𝑏 = 23
𝑥 = 𝑥 𝐿𝐵 + 𝑖
𝑓𝑚 − 𝑓𝑚𝑏
2𝑓𝑚 − 𝑓𝑚𝑎 − 𝑓𝑚𝑏
Modal class

48. Find the Mode for the grouped data.
𝑥 𝐿𝐵 = 64.5 𝑖 = 11 𝑓𝑚 = 55 𝑓𝑚𝑎 = 7 𝑓𝑚𝑏 = 23
𝑥 = 𝑥 𝐿𝐵 + 𝑖
𝑓𝑚 − 𝑓𝑚𝑏
2𝑓𝑚 − 𝑓𝑚𝑎 − 𝑓𝑚𝑏
= 64.5 + 11
55 − 23
2(55) − 7 − 23
𝑥 = 64.5 + 11
32
80
= 64.5 + 11 0.4
𝑥 = 64.5 + 4.4 = 68.9

49. Reference:
• TEACHING GUIDE FOR SENIOR HIGH SCHOOL - Statistics and Probability by CHED in
collaboration with the Philippine NormalUniversity