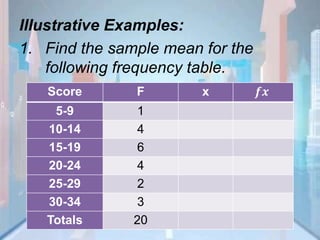
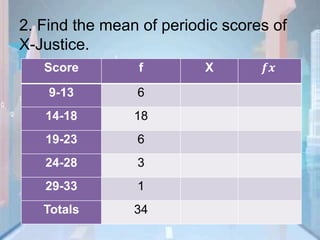
A frequency distribution table was constructed with age ranges and their frequencies for 20 workers. The mean age was calculated by summing the product of each age and its frequency, divided by the total number of workers. The mean age of the 20 workers was 26. Age Range Frequency x fx 18-20 4 8 80 21-23 3 6 18 24-26 3 6 18 28-30 3 6 18 31-33 1 3 3 34-36 1 3 3 37-39 1 3 3 Total 20 143 Mean = Sum(fx) / N = 143

1. Direction: Do as directed.
Problem 1:
Mark operates Technology Titans, a Web site service that
employs 8 people. Find the mean age of his workers if
the ages of the employees are as follows:
55, 63, 34, 59, 29, 46, 51, 41
Problem 2:
Stephen has been working on programing and updating
a Web site for his company for the past 15 months. The
following numbers represent the number of hours
Stephen has worked on this Web site for each of the past
7 months: 24, 25, 31, 50, 53, 66, 78. What is the mean
(average) number of hours that Stephen worked on this
Web site each month?

2. What if you will need to solve for
the mean of large number of data,
is it applicable to use the common
method? Or there is any method to
use in order to solve for the mean
of these data easily?

4. Objectives:
After the discussion, you should be
able to:
1. Calculate the measures of
central tendency of ungrouped
and grouped data.

5. MEAN OF GROUPED DATA
• A grouped data is data that has been
bundled together in categories. The formula
in getting the mean of grouped data is given
as follows:
𝒙 =
𝒇𝒙
𝑵
𝒘𝒉𝒆𝒓𝒆:
𝒙 = 𝒎𝒆𝒂𝒏 ; 𝒇 = 𝒇𝒓𝒆𝒒𝒖𝒆𝒏𝒄𝒚;
𝒙 = 𝒄𝒍𝒂𝒔𝒔 𝒎𝒂𝒓𝒌;
𝑵 = 𝒕𝒐𝒕𝒂𝒍 𝒏𝒖𝒎𝒃𝒆𝒓 𝒐𝒇 𝒅𝒂𝒕𝒂

6. Steps in solving the mean of grouped
data
1) Find the class mark (x) for each class
interval.
2) Multiply the class mark (x) by the
frequency (f).
3) Get the sum of each column frequency
(f) and class mark (x).
4) Substitute the answers in the formula in
getting the mean of grouped data.

7. Illustrative Examples:
1. Find the sample mean for the
following frequency table.
Score F x 𝒇𝒙
5-9 1
10-14 4
15-19 6
20-24 4
25-29 2
30-34 3
Totals 20

8. Solution:
• Find the midpoint (x) for each class
interval.
• Multiply the midpoint (x) by the frequency
(f).
• Get the sum of each column frequency
(f) and midpoint (x).
𝒙 =
𝒇𝒙
𝑵
=
𝟑𝟗𝟓
𝟐𝟎
= 𝟏𝟗. 𝟕𝟓
Therefore, the sample mean is 19.75.

9. 2. Find the mean of periodic scores of
X-Justice.
Score f X 𝒇𝒙
9-13 6
14-18 18
19-23 6
24-28 3
29-33 1
Totals 34

10. Solution:
• Find the midpoint (x) for each class interval.
• Multiply the midpoint (x) by the frequency
(f).
• Get the sum of each column frequency (f)
and midpoint (x).
𝒙 =
𝒇𝒙
𝑵
=
𝟓𝟖𝟗
𝟑𝟒
= 𝟏𝟕. 𝟑𝟐
Therefore, the sample mean is 17.32.

11. What are the steps in
getting the mean of
grouped data?

12. Steps in solving the mean of grouped
data
1) Find the midpoint (x) for each class
interval.
2) Multiply the midpoint (x) by the
frequency (f).
3) Get the sum of each column frequency
(f) and midpoint (x).
4) Substitute the answers in the formula in
getting the mean of grouped data.

13. Reflection of the Mind
and Heart:
“Great minds discuss ideas;
average minds discuss events;
small minds discuss people.” -
Arthur Helps

14. Directions: Do as directed.
Solve:
A class of 40 students took a mock
exam in math. They were given
percentage marks as follows:
73, 45, 62, 34, 59, 20, 48, 50, 78, 38, 52, 91,57,
82, 46, 51, 62, 58,39, 50,72, 73,63,52, 41, 37, 28,
46, 71, 75, 36, 28, 44, 90, 51, 28, 60, 18, 47, 40.
Construct a Frequency Distribution Table and find
the mean.

16. Assignment: Find the mean.
The data shows the ages of 20 workers in
an office.
𝟐𝟑, 𝟑𝟓, 𝟐𝟏, 𝟐𝟎, 𝟐𝟖, 𝟑𝟐, 𝟏𝟗, 𝟑𝟗, 𝟐𝟎, 𝟏𝟖,
𝟑𝟕, 𝟐𝟗, 𝟏𝟗, 𝟐𝟓, 𝟑𝟒, 𝟐𝟔, 𝟐𝟒, 𝟑𝟏, 𝟐𝟐, 𝟑𝟎.
• Make a frequency distribution table.
• Find the mean of the age of workers.