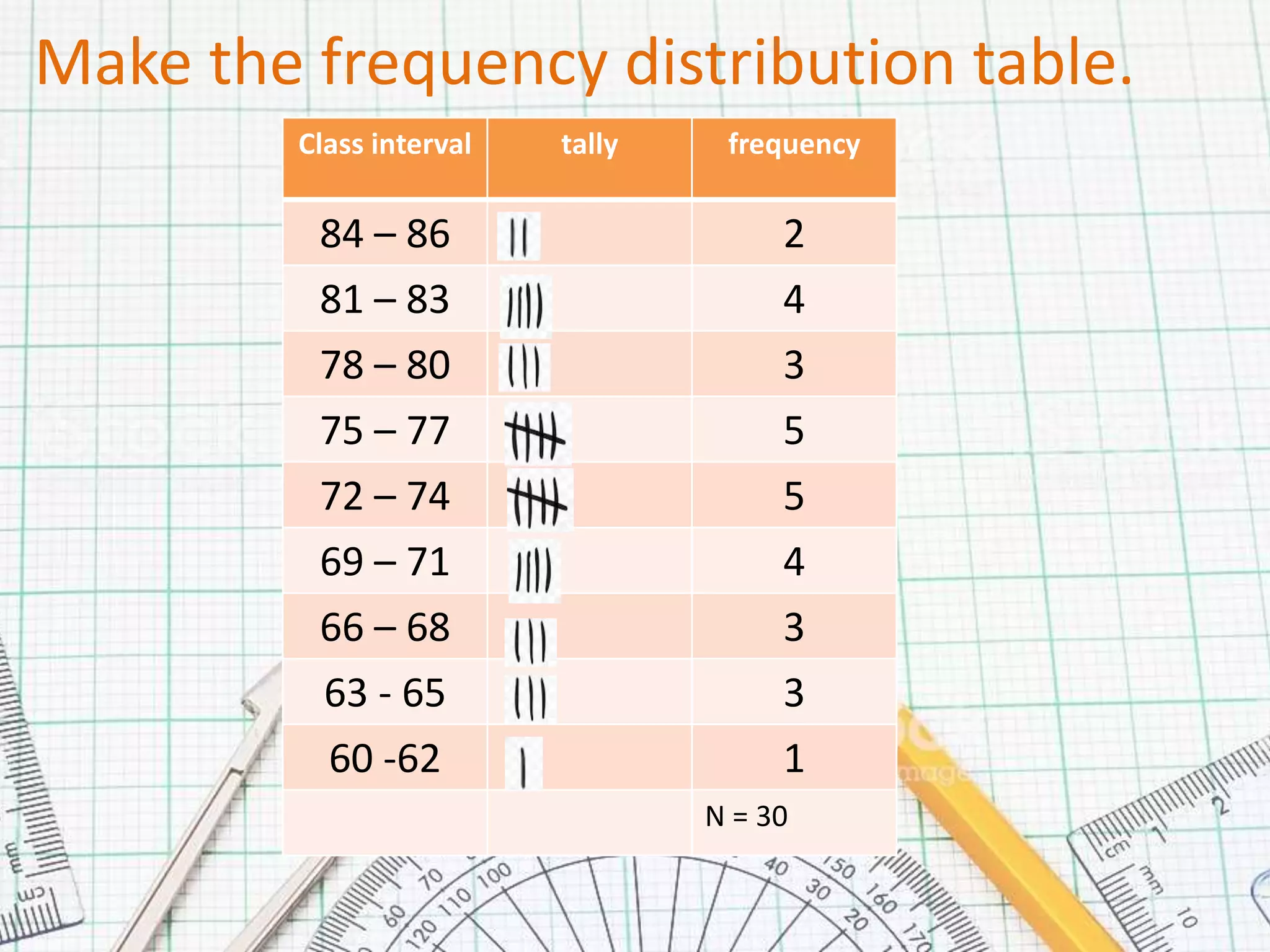
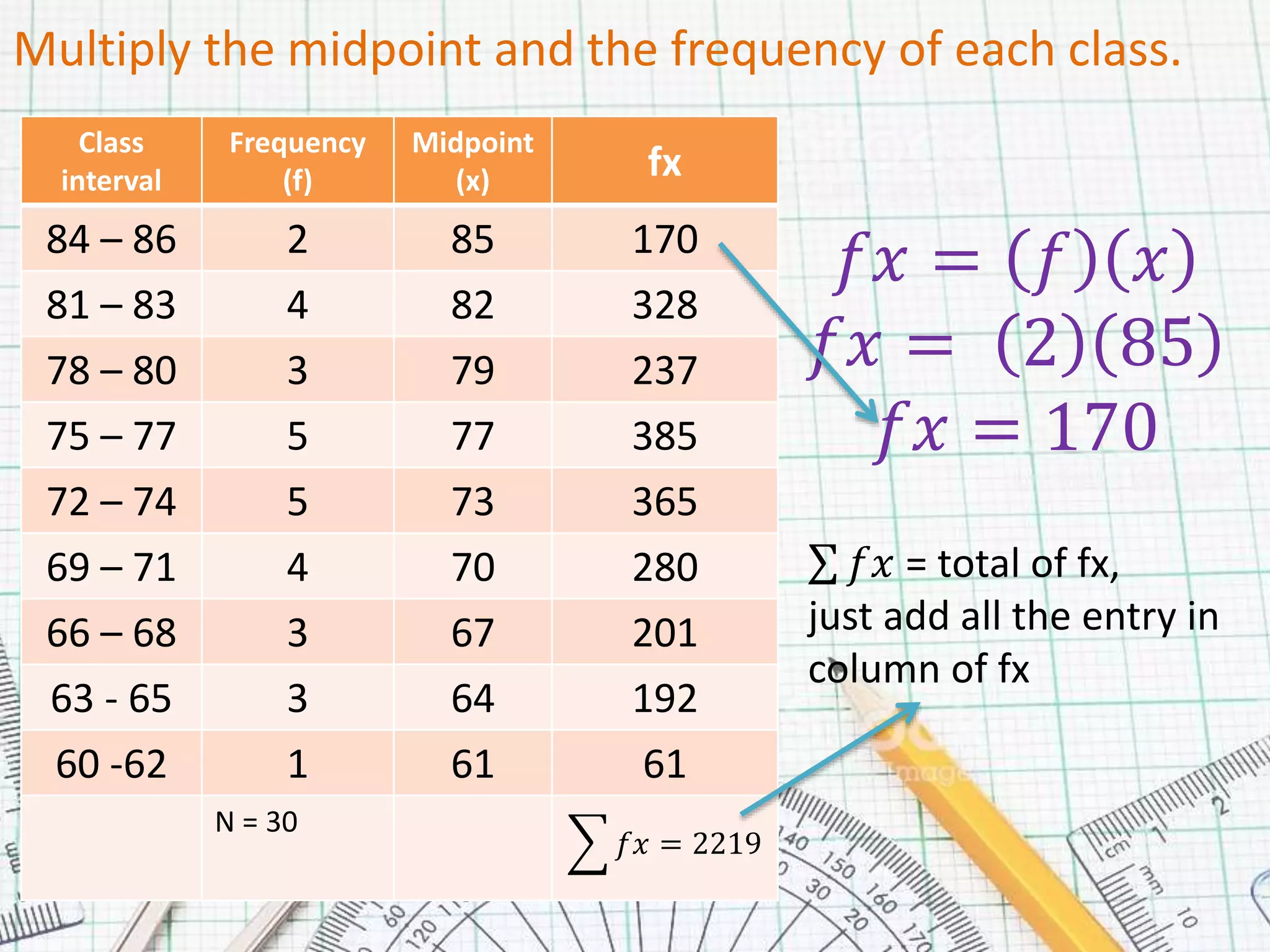
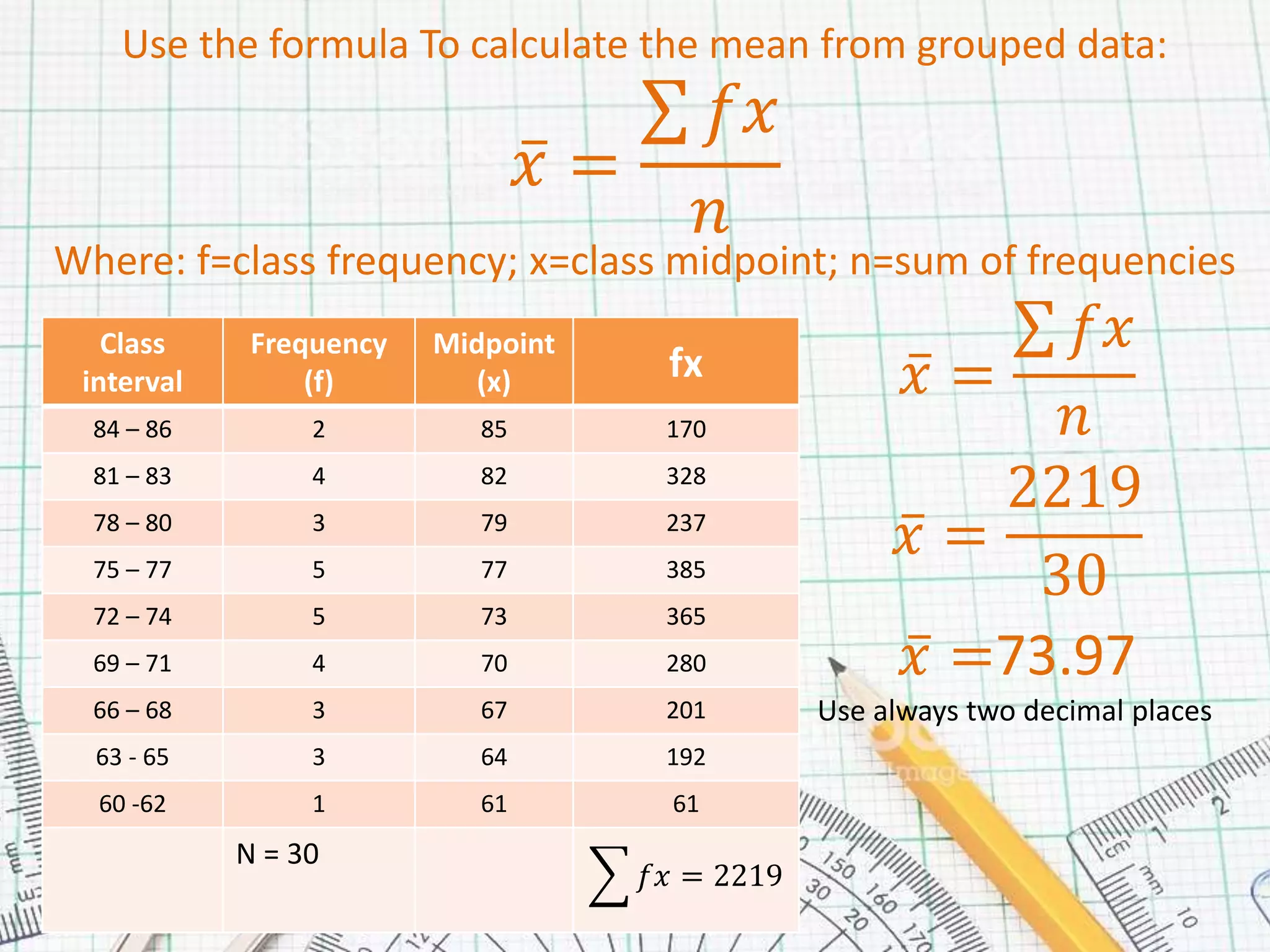
This document provides steps for calculating the mean of grouped data: 1. Make a frequency distribution table with class intervals, frequencies, and midpoints. 2. Multiply the midpoint and frequency for each class to calculate the fx value. 3. Use the formula x=fx/n, where f is the frequency, x is the midpoint, and n is the total frequency, to calculate the mean. For example, given data grouped into classes with frequencies totaling 30, the mean was calculated to be 73.97.

1. MEAN of
Grouped Data
By: Maryleigh P. Castillo

2. Objectives:
• Make frequency distribution
table
• Compute for the Mean

3. Steps in calculating mean of grouped
data
• Make the frequency distribution table.
• Find for the midpoint (x) of each class interval
• Multiply the midpoint and the frequency of
each class.
• Use the formula To calculate the mean from
grouped data: 𝑥 =
𝑓𝑥
𝑛
Where: f=class frequency; x=class midpoint;
n=sum of frequencies

4. Example:
Class interval tally frequency
84 – 86
81 – 83
78 – 80
75 – 77
72 – 74
69 – 71
66 – 68
63 - 65
60 -62
72 75 77 67 72
67 82 76 76 70
61 67 84 69 64
78 65 86 73 81
71 63 72 72 83
78 83 80 71 75

5. Make the frequency distribution table.
Class interval tally frequency
84 – 86 2
81 – 83 4
78 – 80 3
75 – 77 5
72 – 74 5
69 – 71 4
66 – 68 3
63 - 65 3
60 -62 1
N = 30

6. Find for the midpoint (x) of each class interval.
Class interval Frequency
(f)
Midpoint
(x)
84 – 86 2 85
81 – 83 4 82
78 – 80 3 79
75 – 77 5 77
72 – 74 5 73
69 – 71 4 70
66 – 68 3 67
63 - 65 3 64
60 -62 1 61
N = 30
To find midpoint simply add the lower
score and the highest score of each
class interval then divide by 2.
Do it in every class interval.
𝒙 =
𝑳𝑺 + 𝑯𝑺
𝟐
𝒙 =
𝟖𝟒 + 𝟖𝟔
𝟐
𝒙 =
𝟏𝟕𝟎
𝟐
𝒙 = 𝟖𝟓

7. Multiply the midpoint and the frequency of each class.
Class
interval
Frequency
(f)
Midpoint
(x) fx
84 – 86 2 85 170
81 – 83 4 82 328
78 – 80 3 79 237
75 – 77 5 77 385
72 – 74 5 73 365
69 – 71 4 70 280
66 – 68 3 67 201
63 - 65 3 64 192
60 -62 1 61 61
N = 30
𝑓𝑥 = 2219
𝑓𝑥 = 𝑓 𝑥
𝑓𝑥 = 2 85
𝑓𝑥 = 170
𝑓𝑥 = total of fx,
just add all the entry in
column of fx

8. Use the formula To calculate the mean from grouped data:
𝑥 =
𝑓𝑥
𝑛
Where: f=class frequency; x=class midpoint; n=sum of frequencies
Class
interval
Frequency
(f)
Midpoint
(x) fx
84 – 86 2 85 170
81 – 83 4 82 328
78 – 80 3 79 237
75 – 77 5 77 385
72 – 74 5 73 365
69 – 71 4 70 280
66 – 68 3 67 201
63 - 65 3 64 192
60 -62 1 61 61
N = 30
𝑓𝑥 = 2219
𝑥 =
𝑓𝑥
𝑛
𝑥 =
2219
30
𝑥 =73.97
Use always two decimal places