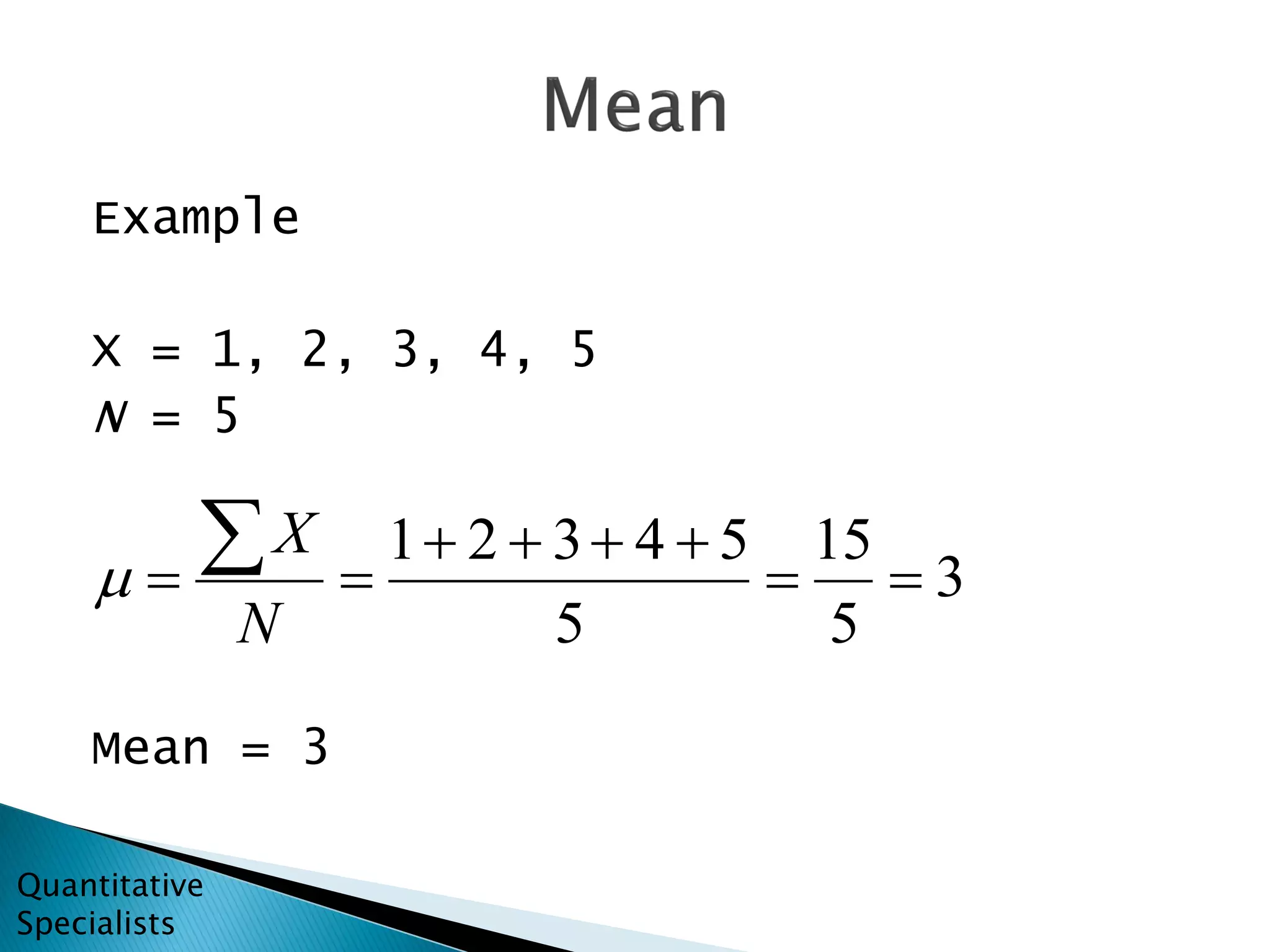
The document defines and provides examples for mode, median, and mean - three common measures of central tendency used in statistics. Mode is defined as the most frequently occurring value, median is defined as the middle value when values are ordered from lowest to highest, and mean is defined as the arithmetic average calculated by summing all values and dividing by the total number of values. Special considerations are discussed for calculating the median when the number of values is even versus odd. The document encourages the viewer to subscribe to the Quantitative Specialists YouTube channel for more statistics content and courses.

1. Quantitative Specialists

2. Mode – the most frequently occurring
score
Median – the middle score
Mean – the arithmetic average
Quantitative
Specialists

3. The most frequently occurring score
Example: 1, 2, 2, 2, 3, 3, 4
Mode = 2
Quantitative
Specialists

4. Example: 1, 2, 2, 3, 3, 4
Bimodal (two modes) = 2, 3
Quantitative
Specialists

5. Example: 1, 2, 2, 3, 3, 4, 4
Multimodal (three or more modes) = 2,
3, 4
Quantitative
Specialists

6. The middle value
Example: 1, 2, 3, 4, 5
Median = 3
Quantitative
Specialists

7. Example: 1, 2, 3, 4, 5, 6
Two middle scores: 3, 4
To find the median, take the average
of the two middle scores: (3+4)/2 =
3.5
Median = 3.5
Quantitative
Specialists

8. Odd N: When there are an odd number of
values, the median is the middle
score
(1, 2, 3, 4, 5; N=5) median = 3
Even N: When there are an even number
of values, the median is equal to the
average of the two middle scores
(1, 2, 3, 4, 5, 6; N=6) median = 3.5
Quantitative
Specialists

9. Prior to calculating the median, be
sure that the numbers are ordered
from smallest to largest (don’t
pick the middle number of a set of
numbers if they are not first
ordered)
Example: 2, 3, 1, 3, 1, 6
Reordered: 1, 1, 2, 3, 3, 6
Median = 2.5
Quantitative
Specialists

10. Mean = the arithmetic average
Mean:
Where µ = the population mean, ΣX is
the sum of the variable X (add the
values of X together), and N is the
total number of values
N
X
Quantitative
Specialists

11. Example
X = 1, 2, 3, 4, 5
N = 5
Mean = 3
3
5
15
5
54321




N
X

Quantitative
Specialists

12. YouTube Channel: Quantitative Specialists
Subscribe to our channel at:
https://www.youtube.com/statisticsinstructor
(typing “quantitative specialists” in the search box will also find
us). New videos uploaded regularly.
Comprehensive statistics courses available on
Udemy.com. Search for Quantitative Specialists (use
offer SS50 for a discount on any of our Statistics/SPSS
courses with our thanks for viewing us on slideshare)
Statistical consultation questions? Contact us at:
quantitativespecialists@gmail.com