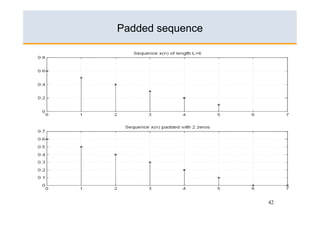
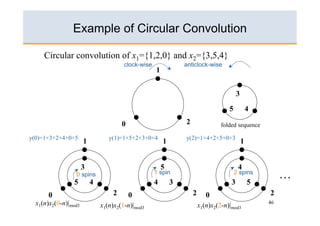
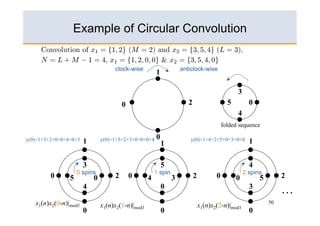
The document discusses concepts related to the Discrete Fourier Transform (DFT) and its applications, focusing on topics like circular convolution, zero-padding, and standard convolution. It explains how DFT can be used for linear filtering by computing standard convolution products. Key points include the transformation of signals into the frequency domain and the numerical equivalent of the Fourier Transform for digital computation.

1. More on DFT
Elena Punskaya
www-sigproc.eng.cam.ac.uk/~op205
Some material adapted from courses by
Prof. Simon Godsill, Dr. Arnaud Doucet,
Dr. Malcolm Macleod and Prof. Peter Rayner
39

2. DFT Interpolation
normalised
40

3. Zero padding
41

4. Padded sequence
42

5. Zero-padding
π
N
43

6. Zero-padding
just visualisation, not additional information! 44

7. Circular Convolution
xxxxxxxxx
m
circular convolution
45

8. Example of Circular Convolution
Circular convolution of x1={1,2,0} and x2={3,5,4}
clock-wise anticlock-wise
1
3
5 4
0 2 folded sequence
y(0)=1×3+2×4+0×5 y(1)=1×5+2×3+0×4 y(2)=1×4+2×5+0×3
1 1 1
3 5 4
0 spins 1 spin 2 spins
…
5 4 4 3 3 5
0 2 0 2 0 2
x1(n)x2(0-n)|mod3 x1(n)x2(1-n)|mod3 x1(n)x2(2-n)|mod3 46

9. Example of Circular Convolution
clock-wise anticlock-wise
47

10. IDFT
m +
+
+
+
+
48

11. Standard Convolution using Circular Convolution
It can be shown that circular
convolution of the padded
sequence corresponds to the
standard convolution
49

12. Example of Circular Convolution
clock-wise anticlock-wise
1
3
0 2 5 0
4
folded sequence
y(0)=1×3+2×0+0×4+0×5 y(0)=1×5+2×3+0×0+0×4 0 y(0)=1×4+2×5+0×3+0×0
1 1 1
3 5 4
0 spins 1 spin 2 spins
0 5 0 2 0 4 3 2 0 0 5 2
4 0 3
…
x1(n)x2(0-n)|mod3 x1(n)x2(1-n)|mod3 x1(n)x2(2-n)|mod3 50
0 0 0

13. Standard Convolution using Circular Convolution
51

14. Proof of Validity
Circular convolution of the padded sequence corresponds to the standard
convolution
52

15. Linear Filtering using the DFT
FIR filter:
Frequency domain equivalent:
DFT and then IDFT can be used to compute standard convolution
product and thus to perform linear filtering.
53

16. Summary So Far
• Fourier analysis for periodic functions focuses on the
study of Fourier series
• The Fourier Transform (FT) is a way of transforming
a continuous signal into the frequency domain
• The Discrete Time Fourier Transform (DTFT) is a
Fourier Transform of a sampled signal
• The Discrete Fourier Transform (DFT) is a discrete
numerical equivalent using sums instead of integrals
that can be computed on a digital computer
• As one of the applications DFT and then Inverse DFT
(IDFT) can be used to compute standard convolution
product and thus to perform linear filtering 54