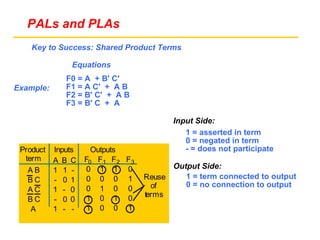
This document summarizes programmable logic devices including PALs and PLAs. It describes how PALs and PLAs can be personalized by making or breaking connections between pre-fabricated AND and OR gates. An example is provided to illustrate how a PAL or PLA can be programmed to implement different logic functions by selectively connecting product terms to outputs. The key differences between PALs and PLAs are also outlined.

1. CS370 – Spring 2003
Programmable Logic Devices
PALs/PLAs

2. PALs and PLAs
Pre-fabricated building block of many AND/OR gates (or NOR, NAND)
"Personalized" by making or breaking connections among the gates
Programmable Array Block Diagram for Sum of Products Form
Inputs
Dense array of Dense array of
AND gates Product OR gates
terms
Outputs

3. PALs and PLAs
Key to Success: Shared Product Terms
Equations
F0 = A + B' C'
Example: F1 = A C' + A B
F2 = B' C' + A B
F3 = B' C + A
Input Side:
1 = asserted in term
0 = negated in term
Product Inputs Outputs - = does not participate
term A B C F0 F1 F2 F3
AB 1 1 - 0 1 1 0 Output Side:
BC - 0 1 0 0 0 1 Reuse 1 = term connected to output
of 0 = no connection to output
AC 1 - 0 0 1 0 0
terms
BC - 0 0 1 0 1 0
A 1 - - 1 0 0 1

4. PALs and PLAs
Example Continued All possible connections are available
before programming
A B C
F0 F1 F2 F3

5. PALs and PLAs
Example Continued
A B C
Unwanted connections are "blown"
AB
/BC
A /C
/B /C
A
Note: some array structures
work by making connections
rather than breaking them F0 F1 F3
F2

6. PALs and PLAs
Alternative representation for high fan-in structures
Short-hand notation
so that all the wires need
not be drawn!
A B C D
AB
AB
Notation for implementing
CD F0 = A B + A' B'
F1 = C D' + C' D
CD
AB+AB CD + CD

7. PALs and PLAs
A B C
Design Example ABC
A
B
C
Multiple functions of A, B, C A
B
F1 = A B C
C
F2 = A + B + C ABC
ABC
F3 = A B C
ABC
F4 = A + B + C ABC
ABC
F5 = A xor B xor C
ABC
F6 = A xnor B xnor C ABC
F1 F2 F3 F4 F5 F6

8. PALs and PLAs
Difference between Programmable Array Logic (PAL) and
Programmable Logic Array (PLA):
PAL concept -- implemented by Monolithic Memories
constrained topology of the OR Array – I.e., the OR
array cannot be fully programmed.
A given column of the OR array
has access to only a subset of
the possible product terms
PLA concept generalized topologies in AND and OR planes

9. PALs and PLAs
Design Example: BCD to Gray Code Converter
Truth Table A B C D W X Y Z K-maps
0 0 0 0 0 0 0 0
0 0 0 1 0 0 0 1 AB
A
AB
A
0 0 1 0 0 0 1 1 CD 00 01 11 10 CD 00 01 11 10
0 0 1 1 0 0 1 0
00 0 0 X 1 00 0 1 X 0
0 1 0 0 0 1 1 0
0 1 0 1 1 1 1 0
01 0 1 X 1 01 0 1 X 0
0 1 1 0 1 0 1 0
D D
0 1 1 1 1 0 1 1 0 1 X X 0 0 X X
11 11
1 0 0 0 1 0 0 1 C C
1 0 0 1 1 0 0 0 10 0 1 X X 10 0 0 X X
1 0 1 0 X X X X
1 0 1 1 X X X X B B
1 1 0 0 X X X X K-map for W K-map for X
1 1 0 1 X X X X
1 1 1 0 X X X X A A
1 1 1 1 X X X X AB AB
CD 00 01 11 10 CD 00 01 11 10
00 0 1 X 0 00 0 0 X 1
Minimized Functions:
01 0 1 X 0 01 1 0 X 0
W=A+BD+BC 11 1 1 X X
D
11 0 1 X X
D
X = B C' C C
Y=B+C 10 1 1 X X 10 1 0 X X
Z = A'B'C'D + B C D + A D' + B' C D' B B
K-map for Y K-map for Z

10. PALs and PLAs A B C D
A
BD
Programmed PAL: BC
0
BC
0
0
0
B
C
0
0
ABCD
BCD
AD
BCD
4 product terms per each OR gate W X Y Z

11. PALs and PLAs
Code Converter Discrete Gate Implementation
A A
A 1
B
4
C
B D
2 3 W
D
B
C 3
B 2 D
C 4 4 Z
A
5
B D 1 D
2
2 1 X B
C 1
C 3
C D
1: 7404 hex inverters
2 Y
B 1 2,5: 7400 quad 2-input NAND
B 3: 7410 tri 3-input NAND
4: 7420 dual 4-input NAND
4 SSI Packages vs. 1 PLA/PAL Package!

12. PALs and PLAs
Example: Magnitude Comparator A B C D
A A ABCD
AB AB
CD 00 01 11 10 CD 00 01 11 10 ABCD
00 1 0 0 0 00 0 1 1 1
ABCD
01 0 1 0 0 01 1 0 1 1
D D
ABCD
11 0 0 1 0 11 1 1 0 1
C C
AC
10 0 0 0 1 10 1 1 1 0
AC
B B
BD
K-map for EQ K-map for NE
BD
A A
AB AB ABD
CD 00 01 11 10 CD 00 01 11 10
00 0 0 0 0 00 0 1 1 1
BCD
ABC
01 1 0 0 0 01 0 0 1 1
D D BCD
11 1 1 0 1 11 0 0 0 0
C C
10 1 1 0 0 10 0 0 1 0
B B
EQ NE LT GT
K-map for LT K-map for GT