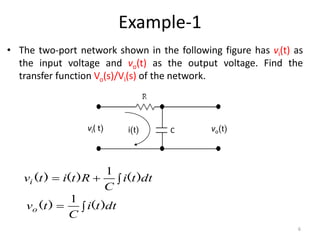
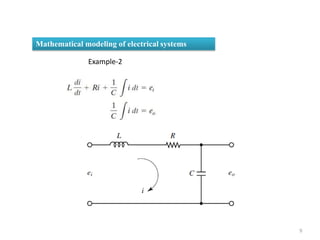
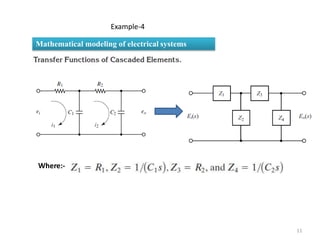
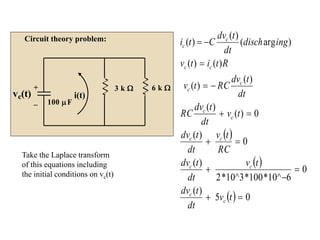
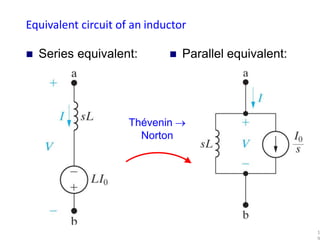
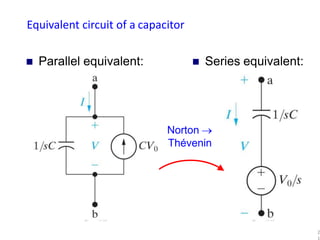
The document provides a comprehensive overview of modeling electrical systems, focusing on the basic elements such as resistors, capacitors, and inductors, including their time-domain expressions and Laplace transforms. It includes solved examples, demonstrating the calculation of transfer functions in two-port networks and analyzing circuits with initial conditions. The text illustrates how to apply Laplace transforms to various circuit theory problems involving electrical components.

1. Modeling of Electrical System
•Basic Elements Modeling-R,L,C
•Solved Examples with RLC circuit
•L, C Modeling with Non-Zero Initial condition
1

2. Modeling of Electrical System
• The time domain expression relating voltage and current for the
resistor is given by Ohm’s law i-e
R
t
i
t
v R
R )
(
)
( 
• The Laplace transform of the above equation is
R
s
I
s
V R
R )
(
)
( 
R
s
I
s
V R
R 
)
(
/
)
(

3. Basic Elements of Electrical Systems
• The time domain expression relating voltage and current for the
Capacitor is given as:
dt
t
i
C
t
v c
c 
 )
(
)
(
1
• The Laplace transform of the above equation (assuming there is no
charge stored in the capacitor) is
)
(
)
( s
I
Cs
s
V c
c
1

Cs
s
I
s
V c
c
1
)
(
/
)
( 

4. Basic Elements of Electrical Systems
• The time domain expression relating voltage and current for the
inductor is given as:
dt
t
di
L
t
v L
L
)
(
)
( 
• The Laplace transform of the above equation (assuming there is no
energy stored in inductor) is
)
(
)
( s
LsI
s
V L
L 
Ls
s
I
s
V L
L 
)
(
/
)
(

5. V-I and I-V relations
5
Component Laplace V-I Relation I-V Relation
Resistor R
Capacitor
Inductor
dt
t
di
L
t
v L
L
)
(
)
( 
dt
t
i
C
t
v c
c 
 )
(
)
(
1
R
t
i
t
v R
R )
(
)
( 
R
t
v
t
i R
R
)
(
)
( 
dt
t
dv
C
t
i c
c
)
(
)
( 
dt
t
v
L
t
i L
L 
 )
(
)
(
1
Ls
Cs
1

6. Example-1
• The two-port network shown in the following figure has vi(t) as
the input voltage and vo(t) as the output voltage. Find the
transfer function Vo(s)/Vi(s) of the network.
6
C
i(t)
vi( t) vo(t)


 dt
t
i
C
R
t
i
t
vi )
(
)
(
)
(
1

 dt
t
i
C
t
vo )
(
)
(
1

7. Example-1
• Taking Laplace transform of both equations, considering initial
conditions to zero.
• Re-arrange both equations as:
7


 dt
t
i
C
R
t
i
t
vi )
(
)
(
)
(
1

 dt
t
i
C
t
vo )
(
)
(
1
)
(
)
(
)
( s
I
Cs
R
s
I
s
Vi
1

 )
(
)
( s
I
Cs
s
Vo
1

Cs
s
I
s
V
s
I
s
CsV
o
o
/
)
(
)
(
)
(
)
(


)
)(
(
)
(
Cs
R
s
I
s
Vi
1



8. Example-1
• .
8
Cs
s
I
s
Vo /
)
(
)
( 
)
)(
(
)
(
Cs
R
s
I
s
Vi
1


)
(
/
)
( s
V
s
V
nction
TransferFu i
o

)
1
)(
(
/
)
(
)
(
)
(
Cs
R
s
I
Cs
s
I
s
V
s
V
i
o


RCs
s
V
s
V
i
o


1
1
)
(
)
(
)
1
(
1
)
(
)
(
Cs
R
Cs
s
V
s
V
i
o



9. Mathematical modeling of electrical systems
9
Example-2

10. Mathematical modeling of electrical systems
10

11. Mathematical modeling of electrical systems
Where:-
11
Example-4

12. Mathematical modeling of electrical systems
12

13. Mathematical modeling of electrical systems
13

14. Mathematical modeling of electrical systems
14

15. Example-4
Use Laplace transforms to find v(t) for t > 0.
+
_
 

t = 0 6 k 
3 k 
100 F
+
_
v(t)
12 V
volts
v 4
)
0
( 

16. Circuit theory problem:
+
_
vc(t) i(t)
3 k 
100 F
6 k 
 
 
  0
5
)
(
0
6
^
10
*
100
*
3
^
10
*
2
)
(
0
)
(
0
)
(
)
(
)
(
)
(
)
(
)
(
)
arg
(
)
(
)
(














t
v
dt
t
dv
t
v
dt
t
dv
RC
t
v
dt
t
dv
t
v
dt
t
dv
RC
dt
t
dv
RC
t
v
R
t
i
t
v
ing
disch
dt
t
dv
C
t
i
c
c
c
c
c
c
c
c
c
c
c
c
c
c
Take the Laplace transform
of this equations including
the initial conditions on vc(t)

17. Circuit theory problem:
)
(
4
)
(
5
4
)
(
0
)
(
5
4
)
(
0
)
(
5
)
(
5
t
u
e
t
v
s
s
V
s
V
s
sV
t
v
dt
t
dv
t
c
c
c
c
c
c










18. An inductor in the s domain
 iv-relation in the time domain
v(t)  L
d
i(t).
dt
 By operational Laplace transform:
Lv(t) LLi(t) L Li(t),
V(s)  LsI(s)  I0  sL I(s)  LI0.
initial current
1

19. Equivalent circuit of an inductor
 Series equivalent:  Parallel equivalent:
Thévenin 
Norton
1

20. A capacitor in the s domain
 iv-relation in the time domain
i(t)  C
d
v(t).
dt
 By operational Laplace transform:
Li(t) LCv(t) C  Lv(t),
 I(s)  C sV(s) V0  sC V (s)  CV0.
initial voltage
2

21. Equivalent circuit of a capacitor
 Parallel equivalent:  Series equivalent:
Norton 
Thévenin
2