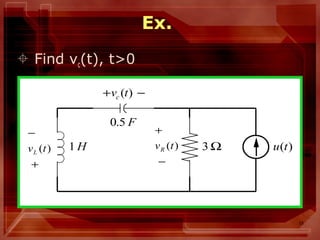
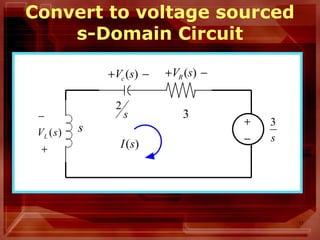
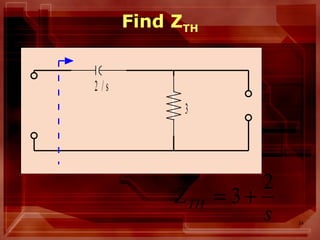
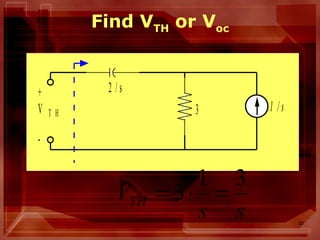
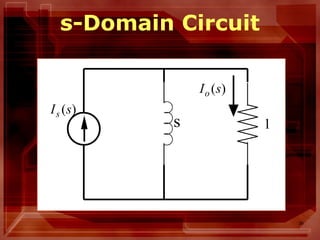
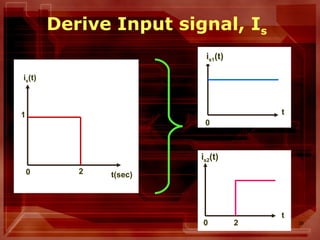
This document describes circuit analysis using Laplace transforms. It discusses analyzing both linear and nonlinear circuits in the Laplace domain. Key steps include taking the Laplace transform of circuit elements and sources, setting up equations for elements like resistors, inductors and capacitors in the s-domain, and using circuit analysis techniques like KVL, KCL to solve for output variables. It also addresses analyzing circuits with both zero and non-zero initial conditions. Examples are provided to illustrate the process.

1. 1
CIRCUIT ANALYSIS
USING LAPLACE
TRANSFORM

2. 2
METHODOLOGY
Examples of nonlinear
circuits:
logic circuits, digital circuits,
or any circuits where the
output is not linearly
proportional to the input.
Examples of linear circuits:
amplifiers, lots of OPM
circuits, circuits made of
passive components (RLCs).
If the circuit is a linear circuit
Laplace transform of the sources
of excitation: s(t) → S(s)
Laplace transform of the all the
elements in the circuit
Find the output O(s) in the
Laplace freq. domain
Obtain the time response O(t) by
taking the inverse Laplace
transform
Stop or approximate
the circuit into a linear
circuit and continue
NO
YES

3. 3
THE s-DOMAIN CIRCUITS
 Equation of circuit analysis:
integrodifferential equations.
 Convert to phasor circuits for AC
steady state.
 Convert to s-domain using Laplace
transform.
 KVL, KCL, Thevenin,etc.

4. 4
KIRCHHOFF’S VOLTAGE LAW
 Consider the KVL in time domain:
 Apply the Laplace transform:
0)()()()( 4321 =++++ tvtvtvtv
0)()()()( 4321 =++++ sVsVsVsV

5. 5
KIRCHHOFF’S CURRENT LAW
 Consider the KCL in time domain:
 Apply the Laplace transform:
0)()()()( 4321 =++++ tItItItI
0)()()()( 4321 =++++ titititi

6. 6
OHM’S LAW
 Consider the
Ohm’s Law in
time domain 
 Apply the
Laplace
transform 
RsIsV RR )()( =
Rtitv RR )()( =

7. 7
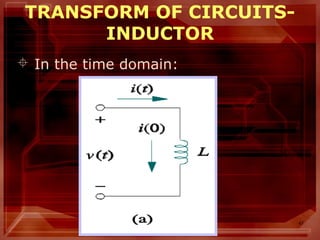
INDUCTOR
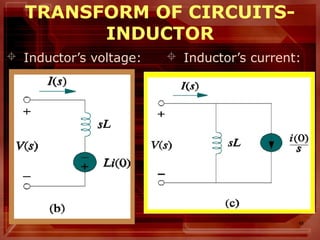
 Inductor’s voltage
– In the time domain:
– In the s-domain:
dt
di
LtvL =)(
)]0()([)( −
−= LLL issILsV

8. 8
INDUCTOR
 Inductor’s current
– Rearrange VL(s) equation:
s
i
sL
sV
sI L
L
)0()(
)(
−
+=

9. 9
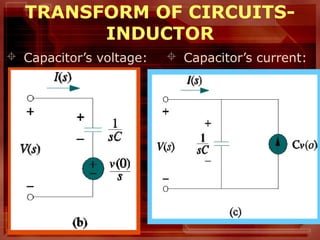
CAPACITOR
 Capacitor’s current
– In the time domain:
– In the s-domain:
dt
dv
Ctic =)(
)]0()([ −
−= ccc vssVC(s)I

10. 10
CAPACITOR
 Capacitor’s voltage
– Rearranged IC(s) equation:
( ) ( ) )(v
s
(s)I
sC
(s)V ccc
−
+= 011

11. 11
RLC VOLTAGE
 The voltage across the RLC elements
in the s-domain is the sum of a term
proportional to its current I(s) and a
term that depends on its initial
condition.
)]0()([)( −
−= LLL issILsV
( ) ( ) )(v
s
(s)I
sC
(s)V ccc
−
+= 011

12. 12
CIRCUIT ANALYSIS FOR
ZERO INITIAL
CONDITIONS (ICs = 0)

13. 13
IMPEDANCE
 If we set all initial conditions to zero,
the impedance is defined as:
[all initial conditions=0]
)(
)()(
sI
sVsZ =

14. 14
IMPEDANCE & ADMITANCE
 The impedances in
the s-domain are
 The admittance is
defined as:
sC
sZ
sLsZ
RsZ
C
L
R
1
)(
)(
)(
=
=
=
sCsY
sL
sY
R
sY
C
L
R
=
=
=
)(
1
)(
1
)(

15. 15
Ex.
 Find vc(t), t>0
H1
F5.0
Ω3 )(tu
−+ )(tvc
+
−
)(tvL
−
+
)(tvR

16. 16
Obtain s-Domain Circuit
 All ICs are zero since there is no
source for t<0
s
s
2
3
s
1
−+ )(sVc
+
−
)(sVL
−
+
)(sVR
)(sI

17. 17
Convert to voltage sourced
s-Domain Circuit
s
s
2
3
s
3
−+ )(sVc
+
−
)(sVL
−+ )(sVR
)(sI −
+

18. 18
23
3
)(
0
3
)(3
2
2
++
−
=⇒
=+





++
ss
sI
s
sI
s
s:KVLBy
Find I(s)

19. 19
Find Capacitor’s Voltage
 The capacitor’s voltage:
 Rewritten:
)23(
6
)(
2
)( 2
++
−
=⋅=
sss
sI
s
sVc
)2)(1(
6
)23(
6
)( 2
++
−
=
++
−
=
ssssss
sVc

20. 20
Using PFE
 Expanding Vc(s) using PFE:
 Solved for K1, K2, and K3:
21)2)(1(
6
)( 321
+
−
+
+=
++
−
=
s
K
s
K
s
K
sss
sVc
2
3
1
63
)2)(1(
6
)(
+
−
+
+
−
=
++
−
=
ssssss
sVc

21. 21
Find v(t)
 Using look up table:
2
3
1
63
)2)(1(
6
)(
+
−
+
+
−
=
++
−
=
ssssss
sVc
( ) )(363)( 2
tueetv tt
c
−−
−+−=

22. 22
Ex.
 Find the Thevenin and Norton
equivalent circuit at the terminal of
the inductor.
1 H
0 .5 F
3 Ω u ( t )

23. 23
Obtain s-domain circuit
s
2 / s
3 1 / s

24. 24
Find ZTH
2 / s
3
s
ZTH
2
3+=

25. 25
Find VTH or Voc
2 / s
3 1 / s
+
V T H
-
ss
VTH
31
3 =⋅=

26. 26
Draw The Thevenin Circuit
 Using ZTH and VTH:
2 / s 3
+
- 3 / s

27. 27
Obtain The Norton Circuit
 The norton current is:
2 / s
3
3 / ( 3 s + 2 )
23
3
23
3
+
=
+
==
s
s
s
Z
V
I
TH
TH
N

28. 28
Ex.
 Find v0(t) for t>0.

29. 29
s-Domain Circuit Elements
Laplace
transform
all
circuit’s
elements
ssC
s
F
ssLH
tu
31
3
1
1
1
)(
=→
=→
→

30. 30
s-Domain Circuit

31. 31
Apply Mesh-Current
Analysis
21
3
5
3
1
1
I
s
I
s
−





+=Loop 1
Loop 2
( ) 2
2
1
21
35
3
1
3
5
3
0
IssI
I
s
sI
s
++=∴






+++−=

32. 32
Substitute I1 into eqn loop 1
( )
( )
sss
I
Isss
I
s
Iss
s
188
3
1883
3
35
3
1
5
3
1
1
232
2
23
22
2
++
=∴
++=






−++





+=

33. 33
Find V0(s)
22
2
20
)2()4(
2
2
3
188
3
)(
++
=
++
=
=
s
ss
sIsV

34. 34
Obtain v0(t)
tetv t
2sin
2
3
)( 4
0
−
=
22
)2()4(
2
2
3
)(
++
=
s
sVo

35. 35
Ex.
 The input, is(t) for the circuit below is
shown as in Fig.(b). Find i0(t)
1
0 2 t(s)
is(t)
(b)
)(tis
Ω1H1
)(tio
(a)

36. 36
s-Domain Circuit
)(sIs
1s
)(sIo

37. 37
 Using current divider:
)1()(
1
)( →





+
= sI
s
s
sIo

38. 38
1
0 2 t(sec)
is(t)
Derive Input signal, Is
0
t
is1(t)
0 2
t
is2(t)
−

39. 39
Obtain Is(t) and Is(s)
 Expression for is(t):
 Laplace transform of is(t):
)2()()( −−= tututis
( ) )2(1
111
)( 22
→−=−= −− ss
s e
ss
e
s
sI

40. 40
 Substitute eqn. (2) into (1):
11
1
)1(
)1(
)(
2
2
0
+
−
+
=
+
−
=
−
−
s
e
s
ss
es
sI
s
s

41. 41
)2()()( )2(
−−= −−−
tuetueti tt
o
Inverse Laplace
transform

42. 42
CIRCUIT ANALYSIS FOR
NON-ZERO INITIAL
CONDITION (ICs ≠ 0)

43. 43
TIME DOMAIN TO s-DOMAIN
CIRCUITS
 s replaced t in the unknown currents
and voltages.
 Independent source functions are
replaced by their s-domain transform
pair.
 The initial condition serves as a
second element, the initial condition
generator.

44. 44
THE ELEMENTS LAW OF s-
DOMAIN
)0(
1
)(
1
)(
)0()()(
)()(
−
−
+=⇒
−=⇒
=⇒
CCC
LLL
RR
v
sC
sI
sC
sV
LissLIsV
sRIsV

45. 45
THE ELEMENTS LAW OF s-
DOMAIN
)0()()(
)0()(
)(
)(
)(
−
−
−=⇒
+=⇒
=⇒
CC
LL
L
R
R
CvssCVsI
s
i
sL
sV
sI
R
sV
sI

46. 46
TRANSFORM OF CIRCUITS-
RESISTOR
 In the time
domain:
 In the s-domain:
i ( t ) + v ( t ) -
R
v ( t ) = i ( t ) R
I ( s ) + V ( s ) -
R
V ( s ) = I ( s ) R

47. 47
TRANSFORM OF CIRCUITS-
INDUCTOR
 In the time domain:

48. 48
TRANSFORM OF CIRCUITS-
INDUCTOR
 Inductor’s voltage:  Inductor’s current:

49. 49
TRANSFORM OF CIRCUITS-
CAPACITOR
 In the time domain:

50. 50
TRANSFORM OF CIRCUITS-
INDUCTOR
 Capacitor’s voltage:  Capacitor’s current:

51. 51
Ex.
 Find v0(t) if the initial voltage is given
as v0(0-
)=5 V

52. 52
s-Domain Circuit

53. 53
Apply nodal analysis method
5.2
1
1
)2(
10
1
5.2
10101
1
10
5.02
1010
0
10
)1(
10
0
+
+
=+⇒
=++
+
−⇒
+=++
− +
s
sV
sVV
s
V
VVV
o
oo
s
oos

54. 54
Cont’d
)2)(1(
3525
25
1
10
)2(
0
++
+
=∴
+
+
=+
ss
s
V
s
sVo

55. 55
Using PFE
 Rewrite V0(s) using PFE:
 Solved for K1 and K2:
21)2)(1(
3525 21
+
+
+
=
++
+
=
s
K
s
K
ss
s
Vo
15;10 21 == KK

56. 56
Obtain V0(s) and v0(t)
 Calculate V0(s):
 Obtain V0(t) using look up table:
2
15
1
10
)(
+
+
+
=
ss
sVo
)()1510()( 2
tueetv tt
o
−−
+=