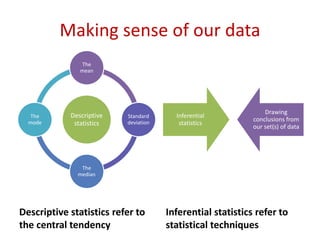
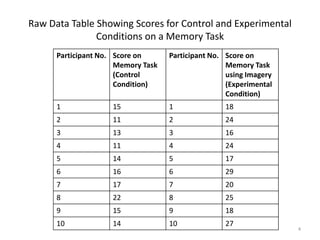
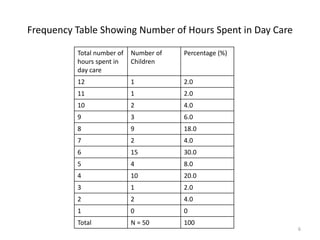
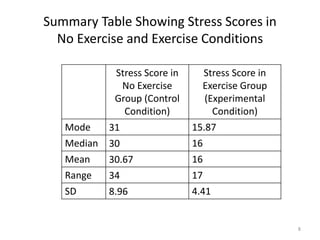
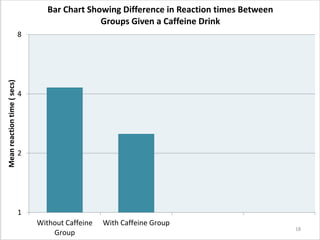
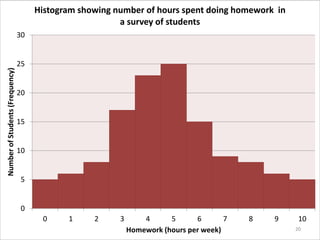
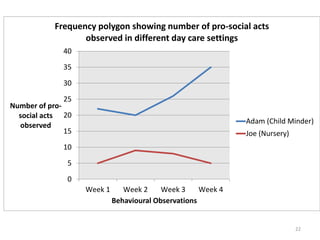
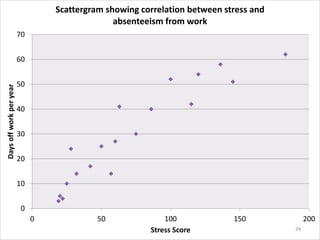
This document provides an overview of descriptive statistics and data representation techniques. It discusses measures of central tendency including the mean, median, and mode. It also covers different ways to present quantitative data visually, including graphs, tables, scatterplots, bar charts, histograms, and frequency polygons. The key purposes of descriptive statistics and data representation are to summarize patterns in data sets and communicate information effectively.

1. Data representation & analysis
• Descriptive statistics: measures of central
tendency – mean, median, mode, calculation
of mean, median and mode.
• Presentation and display of quantitative data:
graphs, tables, scattergrams, bar charts.
• Introduction to statistical testing: the sign test.
1

2. Making sense of our data
Descriptive statistics refer to
the central tendency
Inferential statistics refer to
statistical techniques
Descriptive
statistics
The
mean
Standard
deviation
The
median
The
mode
Inferential
statistics
Drawing
conclusions from
our set(s) of data

3. Tables of Raw Data
• Show scores prior to analysis
• Hard to identify patterns in the data
• Raw data cannot tell us much
3

4. Participant No. Score on
Memory Task
(Control
Condition)
Participant No. Score on
Memory Task
using Imagery
(Experimental
Condition)
1 15 1 18
2 11 2 24
3 13 3 16
4 11 4 24
5 14 5 17
6 16 6 29
7 17 7 20
8 22 8 25
9 15 9 18
10 14 10 27
Raw Data Table Showing Scores for Control and Experimental
Conditions on a Memory Task
4

5. Frequency Tables
• More useful than a raw data table
• Can organise the values into groups when
there are a large number of them, e.g., a 24-
hour period could be organised into 3-hour
segments of 8 values
• Patterns in the data are clearer
5

6. Frequency Table Showing Number of Hours Spent in Day Care
Total number of
hours spent in
day care
Number of
Children
Percentage (%)
12 1 2.0
11 1 2.0
10 2 4.0
9 3 6.0
8 9 18.0
7 2 4.0
6 15 30.0
5 4 8.0
4 10 20.0
3 1 2.0
2 2 4.0
1 0 0
Total N = 50 100
6

7. Summary Tables
• Include:
Measures of central tendency – mean,
median, mode
Measures of dispersion – range, standard
deviation
• Provide a clear
summary of data
7

8. Summary Table Showing Stress Scores in
No Exercise and Exercise Conditions
Stress Score in
No Exercise
Group (Control
Condition)
Stress Score in
Exercise Group
(Experimental
Condition)
Mode 31 15.87
Median 30 16
Mean 30.67 16
Range 34 17
SD 8.96 4.41
8

9. 9
The mean is the average
of a set of data.
It is calculated by adding
up all the numbers in a
set of data and then
dividing them by the total
number.

10. 1. Starts from true zero, e.g., physical quantities
such as time, height, weight
2. Are on a scale of fixed units separated by equal
intervals that allow us to make accurate comparisons,
e.g., someone completing a memory task in 20
seconds did it twice as fast as someone taking 40
seconds
The mean makes use of all the data.
The mean can only be used to measure
data that:
The mean is also
affected by extreme
scores

11. 11
Extreme scores
• Time in seconds to solve a puzzle:
• 135, 109, 95, 121, 140
• Mean = 600 secs ÷ 5 participants =120 secs
• Add a 6th participant, who stares at it for 8 mins
• 135, 109, 95, 121, 140, 480
• Mean = 1080÷6=180 secs

12. 12
Median
• The middle value of scores arranged in an
ordered list.
• It is not affected by extreme scores.
• It is not as sensitive as the mean because
not all scores are reflected in the median.

13. 13
Mode
• The mode is the value that is most common in a data set,
e.g.,2, 4, 6, 7, 7, 7, 10,12 mode = 7.
• It is useful when the data is in categories, such as the
number of people who like blue, read books, play a musical
instrument.
• Not useful if there are many numbers that are the same.

14. 14
Disadvantages of the Mode
 Small changes can make a big difference, e.g.,
1. 3, 6, 8, 9, 10, 10 mode=10
2. 3, 3, 6, 8, 9, 10 mode=3
 Can be bi/multimodal, e.g.,
3,5,8,8,10,12,16,16,16,20

15. 15
Calculating the mean, median
and mode.
• Complete the worksheet for task 2.

16. Using Graphs to
Represent Data
• Graphs summarize quantitative data
• They act as a visual aid allowing us to see
patterns in a data set
• To communicate information effectively, a graph
must be clear and simple and have:
A title
Each axis labelled
 With experimental data, the IV is placed on the
horizontal x-axis while the DV is on the vertical y-
axis
16

17. Bar Chart
• Used to represent ‘discrete data’ where the data
is in categories, which are placed on the x-axis
• The mean or frequency is on the y-axis
• Columns do not touch and have equal width and
spacing
• Examples:
Differences in males/females on a spatial task
Score on a depression scale before and after
treatment
17

18. 1
2
4
8
Without Caffeine
Group
With Caffeine Group
Meanreactiontime(secs) Bar Chart Showing Difference in Reaction times Between
Groups Given a Caffeine Drink
18

19. Histogram
• Used to represent data on a ‘continuous’ scale
• Columns touch because each one forms a
single score (interval) on a related scale, e.g.,
time - number of hours of homework students
do each week
• Scores (intervals) are placed on the x-axis
• The height of the column shows the frequency
of values, e.g., number of students in each
interval – this goes on the y-axis
19

20. 0
5
10
15
20
25
30
0 1 2 3 4 5 6 7 8 9 10
NumberofStudents(Frequency)
Homework (hours per week)
Histogram showing number of hours spent doing homework in
a survey of students
20

21. Frequency Polygon
• Can be used as an alternative to the histogram
• Lines show where mid-points of each column
on a histogram would reach
• Particularly useful for comparing two or more
conditions simultaneously
21

22. 0
5
10
15
20
25
30
35
40
Week 1 Week 2 Week 3 Week 4
Number of pro-
social acts
observed
Behavioural Observations
Frequency polygon showing number of pro-social acts
observed in different day care settings
Adam (Child Minder)
Joe (Nursery)
22

23. Scattergram
• Used for measuring the relationship between
two variables
• Data from one variable is presented on the x-
axis, while the other is presented on the y-axis
• We plot an ‘x’ on the graph where the two
variables meet
• The pattern of plotted points reveals different
types of correlation, e.g., positive, negative or
no relationship
23

24. 0
10
20
30
40
50
60
70
0 50 100 150 200
Daysoffworkperyear
Stress Score
Scattergram showing correlation between stress and
absenteeism from work
24

25. Exam Hints
• You must be able to:
State the strength and direction of a correlation,
e.g., a weak negative correlation or a strong
positive correlation
Interpret information in tables
Interpret information in different types of graphs
Know the most appropriate graph to use to
display a given data set
Correctly label columns and rows on all tables
25

26. Exercise
• Groups of patients with depression were
assessed after six months for the effectiveness
of different treatments. The higher the score the
greater their improvement.
• Choose an appropriate graph to display the
following data:
Treatment Average Improvement
in Symptoms Score
CBT 67
Psychoanalysis 13
ECT 30
Medication 72
26