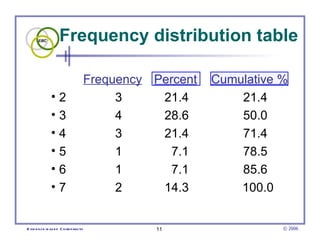
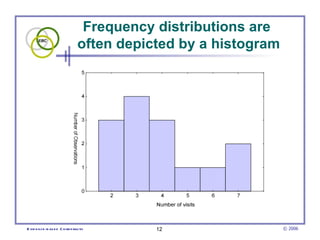
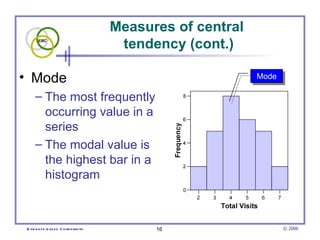
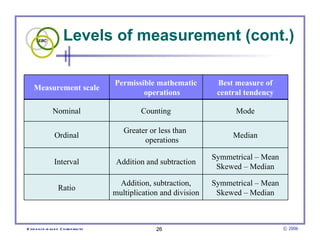
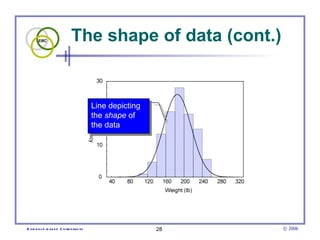
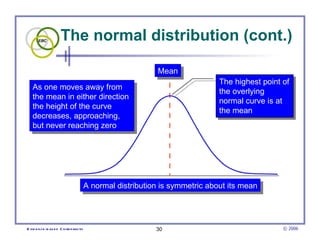
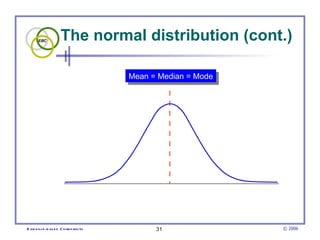
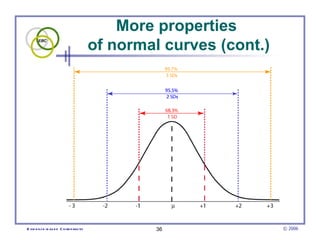
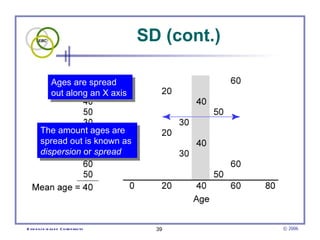
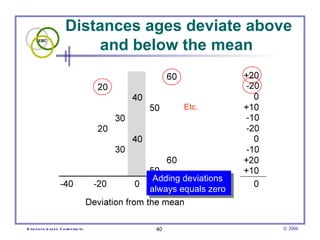
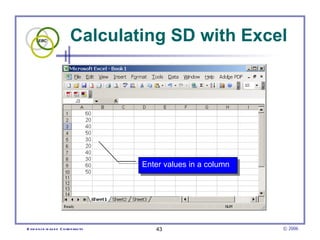
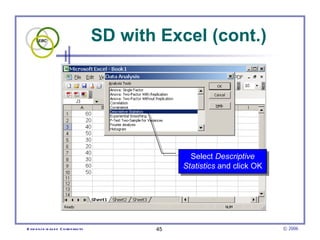
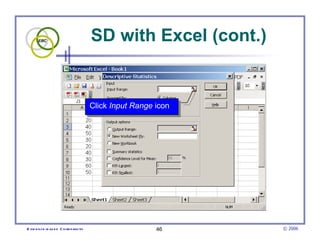
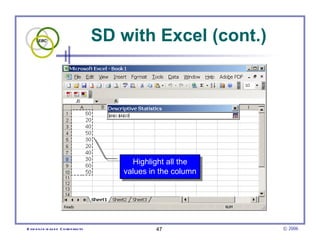
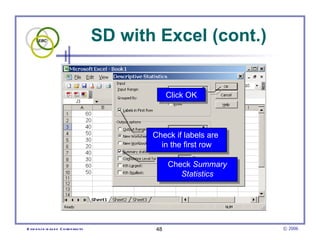
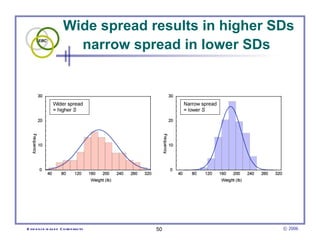
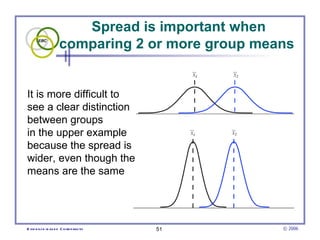
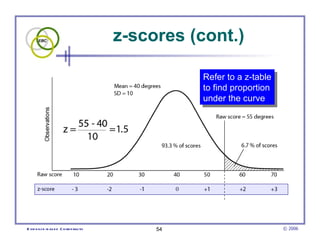
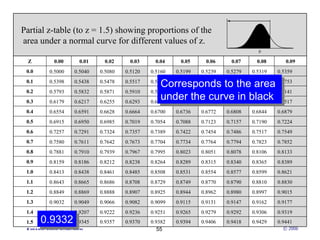
This document provides an introduction to common statistical terms and concepts used in biostatistics. It defines key terms like variables, populations, samples, descriptive statistics, and levels of measurement. It also explains how to calculate measures of central tendency like mean, median, and mode. Additionally, it describes properties of normal and skewed distributions, how to interpret the shape of data, and how to calculate and interpret standard deviation as a measure of variability.

1. Biostatistics Basics An introduction to an expansive and complex field

2. Common statistical terms Data Measurements or observations of a variable Variable A characteristic that is observed or manipulated Can take on different values

3. Statistical terms (cont.) Independent variables Precede dependent variables in time Are often manipulated by the researcher The treatment or intervention that is used in a study Dependent variables What is measured as an outcome in a study Values depend on the independent variable

4. Statistical terms (cont.) Parameters Summary data from a population Statistics Summary data from a sample

5. Populations A population is the group from which a sample is drawn e.g., headache patients in a chiropractic office; automobile crash victims in an emergency room In research, it is not practical to include all members of a population Thus, a sample (a subset of a population) is taken

6. Random samples Subjects are selected from a population so that each individual has an equal chance of being selected Random samples are representative of the source population Non-random samples are not representative May be biased regarding age, severity of the condition, socioeconomic status etc.

7. Random samples (cont.) Random samples are rarely utilized in health care research Instead, patients are randomly assigned to treatment and control groups Each person has an equal chance of being assigned to either of the groups Random assignment is also known as randomization

8. Descriptive statistics ( DSs) A way to summarize data from a sample or a population DSs illustrate the shape , central tendency , and variability of a set of data The shape of data has to do with the frequencies of the values of observations

9. DSs (cont.) Central tendency describes the location of the middle of the data Variability is the extent values are spread above and below the middle values a.k.a., Dispersion DSs can be distinguished from inferential statistics DSs are not capable of testing hypotheses

10. Hypothetical study data (partial from book) Case # Visits 1 7 2 2 3 2 4 3 5 4 6 3 7 5 8 3 9 4 10 6 11 2 12 3 13 7 14 4 Distribution provides a summary of: Frequencies of each of the values 2 – 3 3 – 4 4 – 3 5 – 1 6 – 1 7 – 2 Ranges of values Lowest = 2 Highest = 7 etc.

11. Frequency distribution table Frequency Percent Cumulative % 2 3 21.4 21.4 3 4 28.6 50.0 4 3 21.4 71.4 5 1 7.1 78.5 6 1 7.1 85.6 7 2 14.3 100.0

12. Frequency distributions are often depicted by a histogram

13. Histograms (cont.) A histogram is a type of bar chart, but there are no spaces between the bars Histograms are used to visually depict frequency distributions of continuous data Bar charts are used to depict categorical information e.g., Male–Female, Mild–Moderate–Severe, etc.

14. Measures of central tendency Mean (a.k.a., average ) The most commonly used DS To calculate the mean Add all values of a series of numbers and then divided by the total number of elements

15. Formula to calculate the mean Mean of a sample Mean of a population (X bar) refers to the mean of a sample and refers to the mean of a population  X is a command that adds all of the X values n is the total number of values in the series of a sample and N is the same for a population

16. Measures of central tendency (cont.) Mode The most frequently occurring value in a series The modal value is the highest bar in a histogram Mode

17. Measures of central tendency (cont.) Median The value that divides a series of values in half when they are all listed in order When there are an odd number of values The median is the middle value When there are an even number of values Count from each end of the series toward the middle and then average the 2 middle values

18. Measures of central tendency (cont.) Each of the three methods of measuring central tendency has certain advantages and disadvantages Which method should be used? It depends on the type of data that is being analyzed e.g., categorical, continuous, and the level of measurement that is involved

19. Levels of measurement There are 4 levels of measurement Nominal, ordinal, interval, and ratio Nominal Data are coded by a number, name, or letter that is assigned to a category or group Examples Gender (e.g., male, female) Treatment preference (e.g., manipulation, mobilization, massage)

20. Levels of measurement (cont.) Ordinal Is similar to nominal because the measurements involve categories However, the categories are ordered by rank Examples Pain level (e.g., mild, moderate, severe) Military rank (e.g., lieutenant, captain, major, colonel, general)

21. Levels of measurement (cont.) Ordinal values only describe order, not quantity Thus, severe pain is not the same as 2 times mild pain The only mathematical operations allowed for nominal and ordinal data are counting of categories e.g., 25 males and 30 females

22. Levels of measurement (cont.) Interval Measurements are ordered (like ordinal data) Have equal intervals Does not have a true zero Examples The Fahrenheit scale, where 0° does not correspond to an absence of heat (no true zero) In contrast to Kelvin, which does have a true zero

23. Levels of measurement (cont.) Ratio Measurements have equal intervals There is a true zero Ratio is the most advanced level of measurement, which can handle most types of mathematical operations

24. Levels of measurement (cont.) Ratio examples Range of motion No movement corresponds to zero degrees The interval between 10 and 20 degrees is the same as between 40 and 50 degrees Lifting capacity A person who is unable to lift scores zero A person who lifts 30 kg can lift twice as much as one who lifts 15 kg

25. Levels of measurement (cont.) NOIR is a mnemonic to help remember the names and order of the levels of measurement N ominal O rdinal I nterval R atio

26. Levels of measurement (cont.) Symmetrical – Mean Skewed – Median Addition, subtraction, multiplication and division Ratio Symmetrical – Mean Skewed – Median Addition and subtraction Interval Median Greater or less than operations Ordinal Mode Counting Nominal Best measure of central tendency Permissible mathematic operations Measurement scale

27. The shape of data Histograms of frequency distributions have shape Distributions are often symmetrical with most scores falling in the middle and fewer toward the extremes Most biological data are symmetrically distributed and form a normal curve (a.k.a, bell-shaped curve)

28. The shape of data (cont.) Line depicting the shape of the data

29. The normal distribution The area under a normal curve has a normal distribution (a.k.a., Gaussian distribution) Properties of a normal distribution It is symmetric about its mean The highest point is at its mean The height of the curve decreases as one moves away from the mean in either direction, approaching, but never reaching zero

30. The normal distribution (cont.) Mean A normal distribution is symmetric about its mean As one moves away from the mean in either direction the height of the curve decreases, approaching, but never reaching zero The highest point of the overlying normal curve is at the mean

31. The normal distribution (cont.) Mean = Median = Mode

32. Skewed distributions The data are not distributed symmetrically in skewed distributions Consequently, the mean, median, and mode are not equal and are in different positions Scores are clustered at one end of the distribution A small number of extreme values are located in the limits of the opposite end

33. Skewed distributions (cont.) Skew is always toward the direction of the longer tail Positive if skewed to the right Negative if to the left The mean is shifted the most

34. Skewed distributions (cont.) Because the mean is shifted so much, it is not the best estimate of the average score for skewed distributions The median is a better estimate of the center of skewed distributions It will be the central point of any distribution 50% of the values are above and 50% below the median

35. More properties of normal curves About 68.3% of the area under a normal curve is within one standard deviation (SD) of the mean About 95.5% is within two SDs About 99.7% is within three SDs

36. More properties of normal curves (cont.)

37. Standard deviation (SD) SD is a measure of the variability of a set of data The mean represents the average of a group of scores, with some of the scores being above the mean and some below This range of scores is referred to as variability or spread Variance ( S 2 ) is another measure of spread

38. SD (cont.) In effect, SD is the average amount of spread in a distribution of scores The next slide is a group of 10 patients whose mean age is 40 years Some are older than 40 and some younger

39. SD (cont.) Ages are spread out along an X axis The amount ages are spread out is known as dispersion or spread

40. Distances ages deviate above and below the mean Adding deviations always equals zero Etc.

41. Calculating S 2 To find the average, one would normally total the scores above and below the mean, add them together, and then divide by the number of values However, the total always equals zero Values must first be squared, which cancels the negative signs

42. Calculating S 2 cont. Symbol for SD of a sample  for a population S 2 is not in the same units (age), but SD is

43. Calculating SD with Excel Enter values in a column

44. SD with Excel (cont.) Click Data Analysis on the Tools menu

45. SD with Excel (cont.) Select Descriptive Statistics and click OK

46. SD with Excel (cont.) Click Input Range icon

47. SD with Excel (cont.) Highlight all the values in the column

48. SD with Excel (cont.) Check if labels are in the first row Check Summary Statistics Click OK

49. SD with Excel (cont.) SD is calculated precisely Plus several other DSs

50. Wide spread results in higher SDs narrow spread in lower SDs

51. Spread is important when comparing 2 or more group means It is more difficult to see a clear distinction between groups in the upper example because the spread is wider, even though the means are the same

52. z-scores The number of SDs that a specific score is above or below the mean in a distribution Raw scores can be converted to z-scores by subtracting the mean from the raw score then dividing the difference by the SD

53. z-scores (cont.) Standardization The process of converting raw to z-scores The resulting distribution of z-scores will always have a mean of zero, a SD of one, and an area under the curve equal to one The proportion of scores that are higher or lower than a specific z-score can be determined by referring to a z-table

54. z-scores (cont.) Refer to a z-table to find proportion under the curve

55. z-scores (cont.) 0.9332 Corresponds to the area under the curve in black 0.9441 0.9429 0.9418 0.9406 0.9394 0.9382 0.9370 0.9357 0.9345 0.9332 1.5 0.9319 0.9306 0.9292 0.9279 0.9265 0.9251 0.9236 0.9222 0.9207 0.9192 1.4 0.9177 0.9162 0.9147 0.9131 0.9115 0.9099 0.9082 0.9066 0.9049 0.9032 1.3 0.9015 0.8997 0.8980 0.8962 0.8944 0.8925 0.8907 0.8888 0.8869 0.8849 1.2 0.8830 0.8810 0.8790 0.8770 0.8749 0.8729 0.8708 0.8686 0.8665 0.8643 1.1 0.8621 0.8599 0.8577 0.8554 0.8531 0.8508 0.8485 0.8461 0.8438 0.8413 1.0 0.8389 0.8365 0.8340 0.8315 0.8289 0.8264 0.8238 0.8212 0.8186 0.8159 0.9 0.8133 0.8106 0.8078 0.8051 0.8023 0.7995 0.7967 0.7939 0.7910 0.7881 0.8 0.7852 0.7823 0.7794 0.7764 0.7734 0.7704 0.7673 0.7642 0.7611 0.7580 0.7 0.7549 0.7517 0.7486 0.7454 0.7422 0.7389 0.7357 0.7324 0.7291 0.7257 0.6 0.7224 0.7190 0.7157 0.7123 0.7088 0.7054 0.7019 0.6985 0.6950 0.6915 0.5 0.6879 0.6844 0.6808 0.6772 0.6736 0.6700 0.6664 0.6628 0.6591 0.6554 0.4 0.6517 0.6480 0.6443 0.6406 0.6368 0.6331 0.6293 0.6255 0.6217 0.6179 0.3 0.6141 0.6103 0.6064 0.6026 0.5987 0.5948 0.5910 0.5871 0.5832 0.5793 0.2 0.5753 0.5714 0.5675 0.5636 0.5596 0.5557 0.5517 0.5478 0.5438 0.5398 0.1 0.5359 0.5319 0.5279 0.5239 0.5199 0.5160 0.5120 0.5080 0.5040 0.5000 0.0 0.09 0.08 0.07 0.06 0.05 0.04 0.03 0.02 0.01 0.00 Z Partial z-table (to z = 1.5) showing proportions of the area under a normal curve for different values of z.