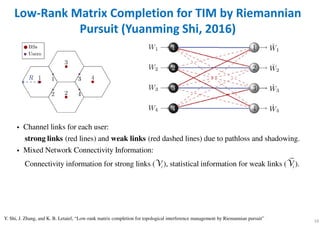
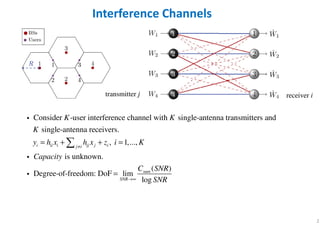
This document discusses topological interference management (TIM) techniques for interference channels. TIM exploits interference alignment principles under realistic channel state information assumptions. The key ideas are: - Focus on canceling strong interference links based on knowledge of the interference pattern - There is a connection between TIM and the index coding problem - The goal of TIM is to maximize degrees of freedom (DoF) based on network topology information - Examples show how transmitting signals over multiple channel uses and exploiting the interference pattern can achieve different DoF values through interference alignment

1. Brief Introduction about
Topological Interference
Management (TIM)
Nov. 26, 2018
Jay Chang
1

2. 2
Interference Channels
transmitter j receiver i
Consider -user interference channel with single-antenna transmitters and
single-antenna receivers.
, 1,...,
is unknown.
Degree-of-freedom: DoF lim
i ii i ij j ij i
SNR
K K
K
y h x h x z i K
Capacity
≠
→
= + + =
=

i
i
i
( )
log
sumC SNR
SNR∞

3. 3
Interference Alignment (Cadambe and Jafar, 2008)
Assume the channel coefficients change over time:
( ) ( ) ( ) ( ) ( ) ( ), 1,...,
Consider channel uses :
(1) (1) (1)
( ) ( ) ( )
i ii i ij j ij i
i ii i
i ii i
y t h t x t h t x t z t i K
T
y h x
y T h T x T
≠
= + + =
     
     =     
         

i
i
⋮ ⋱ ⋮
( )
(1) (1) (1)
( ) ( ) ( )
If we can find precoding matrices and decoding matrices such that
1.
ij j i
j i
ij j i
i ii i ij j ij i
T m m T
i i
i ii i
h x z
h T x T z T
rank m
≠
≠
× ×
     
     + +     
         
= + +
∈ ∈
=

Y H X H X Z
V U
U H V
⋱ ⋮ ⋮
i ℂ ℂ
1 1 , 1 1 , 1 12. ... ... 0
for all 1,..., each user can send symbols interference free across channel uses!
(Thus, DoF ).
When , 1 is achieved by time sh
i i i i i i i i in n
i K m T
m
T K m
− − + +  = 
=
=
= =
U H V H V H V H V
i aring. (DoF 1)=
Cadambe, V., and Jafar, S., ‘Interference alignment and the degrees of freedom of the K user interference channel’, IEEE Trans. Inf. Theory,
2008, 8, pp. 3425–3441

4. 4
Interference Alignment (Cadambe and Jafar, 2008)
( )
1 1 , 1 1 , 1 1
1 11 1 1
1
1.
2. ... ... 0
can we do better than 1?
As an optimization problem :
max
sub
i ii i
i i i i i i i i in n
n
n n nn n
rank m
m
U H H V
rank
U H H V
− − + +
=
  = 
=
      
       =      
            
U H V
U H V H V H V H V
A
⋯
⋱ ⋮ ⋮ ⋱
⋯
ject to a diagonal matrix.
if the diagonal are time-varying and generic then
as , / 2 is almost surely asymptotically achievable. i.e. DoF .
2
ijH
K
T m T
× 
 =  
 × 
→ ∞ = =
A ⋱

5. 5
Topological Interference Management (Jafar, 2014)
• Exploit interference alignment (IA) principles under realistic assumptions on channel state
information at the transmitters (CSIT).
• Knowledge of only the interference pattern at the transmitters. Weak interference links are
negligible, and focusing on canceling strong interference links.
• Tight connection to the index coding problem.
• The problem of studying the DoFs in the partially connected interference channels based on
the network topology information is known as the topological interference management
(TIM) problem.
interference pattern Matrix entry pattern
S. A. Jafar, “Topological interference management through index coding,” IEEE Trans. Inf. Theory, vol. 60, no. 1, pp. 5402-5432, Jan. 2014.

6. 6
Topological Interference Management (Jafar, 2014)
• The following sets of nodes can transmit interference-free: {1,2}, {3,4}, {5}
• For example, {1,2} can transmit in the 1st time slot, {3,4} in the second, and {5} in the
third. Thus, DoF = 1/3.
1 0 0 1 1 0 0 0
1 1 0 0 01 0 0 1 1 0 0 0
0 0 1 1 00 1 0 0 0 1 1 0
0 0 0 0 10 1 0 0 0 1 1 0
0 0 1 0 0 0 0 1
   
   
    
    =
    
     
      
Can we make DoF larger
or minimum matrix rank r
or minimum channel uses N ?
transmit interference-free
transmit interference-free
transmit interference-free
rank = 3

7. 7
Topological Interference Management (Jafar, 2014)
• For example, let each transmitter transmit one signal over two channel uses each:
3 41 5
1 2 3 4 5
32 4
3 34 41
1 11 13 14 1 2 22 23 24 2
3 34 2 4
3 1
3 33 31
3
0
, , , ,
0 0
0
,
0
0
s ss s
X X X X X
ss s
s ss ss
Y h h h Z Y h h h Z
s ss s s
s s
Y h h
s
− −       
= = = = =       
       
− −− −         
= + + + = + + +         
          
−   
= +   
  
45 1 5
35 3 4 44 41 45 4
4
5
5 55 52 5
2
,
0 0 0
0
0
ss s s
h Z Y h h h Z
s
s
Y h h Z
s
−      
+ + = + + +      
      
  
= + +  
   

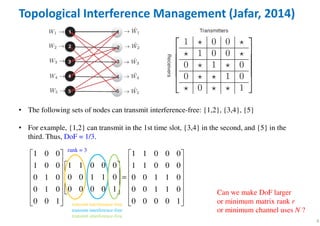
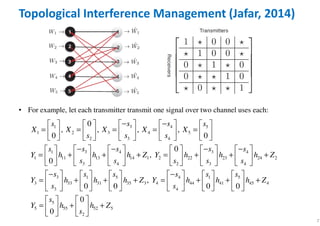
8. 8
• For example, let each transmitter transmit one signal over two channel uses each:
3 41 5
1 2 3 4 5
32 4
3 34 41
1 11 13 14 1 2 22 23 24 2
3 34 2 4
3 1
3 33 31
3
0
, , , ,
0 0
0
,
0
0
s ss s
X X X X X
ss s
s ss ss
Y h h h Z Y h h h Z
s ss s s
s s
Y h h
s
− −       
= = = = =       
       
− −− −         
= + + + = + + +         
          
−   
= +   
  
45 1 5
35 3 4 44 41 45 4
4
5
5 55 52 5
2
,
0 0 0
0
0
ss s s
h Z Y h h h Z
s
s
Y h h Z
s
−      
+ + = + + +      
      
  
= + +  
   
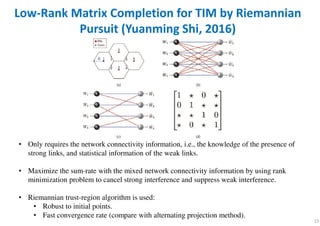
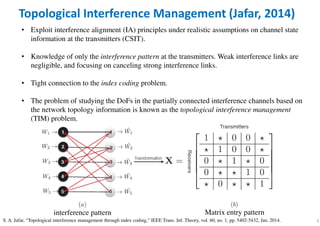
Topological Interference Management (Jafar, 2014)
1 1 1 1 0 0 1
1 1 1 1 0 0 1
1 0 1 1 1
0 1 0 1 1 1 0
0 1 1 1 0
0 1 0 1 1 1 0
1 0 1 0 1 1 1
   
   
   − − 
   = 
    
   
   − −   
DoF = 1/2[ ] [ ] [ ]1 3 5 interference-fre1 1 , 0 1 , 1 0 transmit at the 1st timee slotY Y Y
transmit interference-free
transmit interference-free
rank = 2
Can we make DoF larger
or minimum matrix rank r
or minimum channel uses N ?

9. 9
• Set of all pairs (i, j) such that receiver i has interference from transmitter j.
1 if ,
0 if ( , ) and ,
otherwise.
Suppose we have a rank completion .
Over time slots :
transmitter transmits where is the -th column of and receiv
ij
i i i
i j
A i j S i j
r
r
i s i
=

= ∈ ≠
×
=A UV
v v Vi
( )
er receives
.
receiver decodes by .
where is the -th row of .
i ii i j ij j ij i
i i i ii i j ij j i i i ii i i j ij j i ij i j i
i
i
h s h s z
s h s h s z h s h s z
i
≠
≠ ≠
+ +
+ + = + +

 
v v
u v v u v u v u
u U
i
Topological Interference Management (Jafar, 2014)
• Interference alignment condition without CSIT
is precoding vector and is decoding vector of -th receiver,
is the channel coefficien
0,
t from transmitter to receiver
, interference
.
cancellation
0, 1,...,
H
i j i
r r
i i
ij
H
i i
j j i
i
i
h j i
= ∀ 
=
∈
≠
≠
∈
∈u v
u
v
V
v
uℂ ℂ
. desired message preservationK


 where ( ) denotes the conjugate transposeH
⋅

10. 10
Connection to Low Rank Matrix Completion
1
DoF
r
=
• Challenges :
• What is the minimum possible rank r for a given interference pattern ?
• For a given r, how to find such matrices (if they exist) ?
• How to use low-rank matrix completion approach to solve the TIM problem ?
is precoding vector and is decoding vector of -th receiver,
is the channel coefficient from transmitter to receiver .
0, , interference cancellation
0, 1,...,
r r
i i
ij
H
i j i
H
i i
i
h j i
j j i
i
∈ ∈
= ∀ ∈ ≠ 
≠ =
v u
u v V
u v
ℂ ℂ
, can be rewritten as ( )
. desired message preservation
where [ ] with , is identity matrix, and
: is orthogonal projection operator onto the subspace of
M
M M
ij i Mi
M M M M
K
M M M M
Ω
×
× ×
Ω

=

= ∈ = ×
→

A I
A A I
P
P
ℂ
ℝ ℝ
1 1
matrices i.e.
, if ( , )
( ) .
0, otherwise
assume , [ ] , with [ ,..., ] , [ ,..., ]
we have ( ) .
ij
H H M M H M N N M
i j K K
i j
N M
rank N
Ω
× × ×
∈Ω
= 

≤ = = ∈ = ∈ = ∈
=
A
A
A u v U V U u u V v v
A
P
ℂ ℂ ℂ

11. 11
Connection to Low Rank Matrix Completion
• Low Rank Matrix Completion (LRMC) Problem (non-convex optimization):
• Relaxed to Nuclear Norm Minimization (NNM) Problem (convex optimization):
• Unfortunately, NNM will always return the solution A = I, which is full rank. Because:
• Alternating Optimization Approaches I (non-convex optimization):
minimize ( )
subject to ( ) .
M M
M
rank×
∈
Ω =
A
A
A I
ℝ
P
minimize
subject to ( ) .
where is the sum of the singular values of .
M M
M
× ∗∈
Ω
∗
=
A
A
A I
A A
ℝ
P
( ) ( )Tr( ) Tr TrH H H H
i i i i i i i i i i i i ii i i i i
σ σ σ σ σ ∗
= = = ≤ ≤ =    A u v u v v u v u A
( )
2
,
Express the unknown rank matrix as the product of two smaller matrices i.e.
minimizeM r M r
T
M
F
r
× × Ω
∈ ∈
−
U V
A
UV I
ℝ ℝ
P

12. 12
• Cons:
• Low convergence rate and fails to utilize the second-order information to improve the
convergence rate, e.g., the Hessian of the objective function.
• It requires the optimal rank as a prior information, which is not available in problem LRMC.
Connection to Low Rank Matrix Completion
( )
2
,
minimizeM r M r
T
M
F× × Ω
∈ ∈
−
U V
UV I
ℝ ℝ
P

13. • Alternating Optimization Approaches II (non-convex optimization):
• Instead of searching for the optimal r, seek a completion for a fixed r.
• Matrix Completion Problem:
The matrix A should lie in the sets:
(S1) Rank r matrices
(S2) Matrices with the entry pattern
Observation: project any given matrix onto the sets (S1) and (S2) individually.
Algorithm: Alternating Projection Method.
• Cons:
• The method does not always yield the optimal rank so needs convergence analysis.
13
Connection to Low Rank Matrix Completion
find
subject to ( )
( )rank r
Ω =
=
A
A I
A
P
( )Ω =A IP

14. 14
Connection to Low Rank Matrix Completion
So what’s next ?
• Algorithmic issues: theoretical analysis, fast implementation
• What are good initializations for the various Alternating Projection (AP) methods ?
• Can we give conditions for optimality of the solution of AP method, or performance bounds
otherwise?
• Other matrix completion-based approaches, e.g. Riemannian Pursuit, Bayesian approach ?
• How to combine this with MIMO

15. 15
Low-Rank Matrix Completion for TIM by Riemannian
Pursuit (Yuanming Shi, 2016)
• Only requires the network connectivity information, i.e., the knowledge of the presence of
strong links, and statistical information of the weak links.
• Maximize the sum-rate with the mixed network connectivity information by using rank
minimization problem to cancel strong interference and suppress weak interference.
• Riemannian trust-region algorithm is used:
• Robust to initial points.
• Fast convergence rate (compare with alternating projection method).

16. 16
Low-Rank Matrix Completion for TIM by Riemannian
Pursuit (Yuanming Shi, 2016)
Channel links for each user:
(red lines) and (red dashed lines) due to pathloss and shadowing.
Mixed Network Connectivity Information:
Connectivity information for
strong links weak links
i
i
strong links , statistical information for weak links( ) ( .)i iV V
Y. Shi, J. Zhang, and K. B. Letaief, “Low-rank matrix completion for topological interference management by Riemannian pursuit”

17. 17
Low-Rank Matrix Completion for TIM by Riemannian
Pursuit (Yuanming Shi, 2016)
Proposed: Interference Leakage Minimization
Goal: Achieve high sum rate per channel use with mixed network connectivity information
Proposed Approach: tradeoff of interference leakage and channel use
Low Rank Approach:
Unique Challenges: non-convex, nuclear norm relaxation always yields identity matrix
.H H
i i i ii i i j ij j ij i
y h s h s n≠
= + +u v u v
2 2
2 22
1
1
log(1 ),
HK
i i ii
sum i i
H
i
i i j ijj i
h
C SINR SINR
r hσ=
≠
= + =
+


u v
u u v

18. 18
References
• V. Cadambe, and S. Jafar, ‘Interference alignment and the degrees of freedom of the K user
interference channel’, IEEE Trans. Inf. Theory, 2008, 8, pp. 3425–3441
• S. A. Jafar, “Topological interference management through index coding,” IEEE Trans. Inf. Theory,
vol. 60, no. 1, pp. 529–568, Jan 2014.
• Y. Shi, J. Zhang, and K. B. Letaief, “Low-rank matrix completion for topological interference
management by Riemannian pursuit,” IEEE Trans. Wireless Comm., vol. PP, no. 99, pp. 1–1, 2016.
• B. Hassibi, “Topological interference alignment in wireless networks,” Smart Antennas Workshop,
Aug. 2014.

19. 19
Thank you for your attention

20. 20