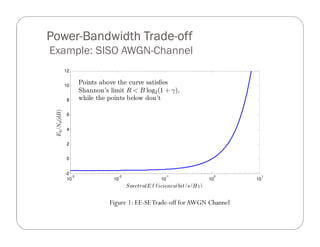
The document discusses the power-bandwidth tradeoff in MIMO systems. It begins with background on MIMO systems, including their structure and key performance improvements like spatial multiplexing gain and diversity gain. It then defines spectral efficiency and energy efficiency, noting that maximizing both is not possible due to the inherent tradeoff between them known as the EE-SE tradeoff. The concept of this tradeoff is explained through mathematical formulations. As an example, the EE-SE tradeoff for an AWGN channel is shown. Approximation methods for determining the EE-SE tradeoff in MIMO systems are also presented.

1. The Power-Bandwidth Tradeoff in
MIMO Systems
Marwan A. Hammouda
August 15, 2012

2. The Purpose of this Presentation ..
The purpose of this presentation is to highlight the concept of
power-bandwidth trade-off in MIMO systems.
Methods/techniques might be used to optimize/deal with
this trade-off are out of the scope.

3. Agenda
MIMO Systems
Background
System Structure
Performance Improvements
• Power-Bandwidth Trade-off
The Concept
Example: SISO AWGN-Channel
EE-SE Trade-off for MIMO System
• EE-ES Trade-off for MIMO Systems
MIMO Capacity
EE-SE Approximations – 1
EE-SE Approximations – 2
Simulation Results
Discussion
• Conclusions
• References

4. MIMO Systems
Background
Four Basic Models:

5. MIMO Systems
System Structure
h11
s1 y1
h12
s2 . y2
User data stream User data stream
. .
. .
. Channel
. .
sm Matrix H yn
s y
Transmitted vector y = Hs + n Received vector
m
h11 h21 …….. hm1 hij is a Complex Gaussian
random variable that models
h12 h22 …….. hm2
Where H = n fading gain between the ith
. . …….. . transmit and jth receive antenna
h1n h2n …….. hmn

6. MIMO Systems
Performance Improvements
1. Spatial multiplexing gain spectral efficiency
Yields a linear (in the minimum of the number of transmit
and receive antennas) increase in capacity for no additional
power or bandwidth expenditure
The corresponding gain is realized by simultaneously
transmitting independent data streams in the same frequency
band.
In rich scattering environments, the receiver exploits
differences in the spatial signatures of the multiplexed
streams to separate the different signals, thereby realizing a
capacity gain.

7. MIMO Systems
Performance Improvements
1. Spatial multiplexing gain

8. MIMO Systems
Performance Improvements
2. Diversity gain link reliability
A powerful technique to mitigate fading and increase
robustness to interference
Principle: provide the receiver with multiple identical
copies of a given signal over (ideally) independent fading
paths.
Intuitively, the more independently fading, identical copies
of a given signal the receiver is provided with, the faster the
bit error rate (BER) decreases as a function of the per signal
SNR.

9. MIMO Systems
Performance Improvements
2. Diversity gain
At high SNR values, it has been shown that.
where d represents the diversity gain and the coding gain.
Definition: For a given transmission rate R, the diversity gain
is:
Where is the BER at the given rate and SNR.

10. MIMO Systems
Performance Improvements
3. Array gain power efficiency
Achieved in MIMO systems through the enhancement of
average signal-to-noise ratio (SNR) due to the transmission
and reception by multiple antennas.
Availability of channel state information (CSI) at the
transmitter/receiver is necessary to realize transmit/receive
array gains.
Principle: To obtain the full array gain, one should transmit
using the maximum eigenmode of the channel

11. MIMO Systems
Performance Improvements
3. Array gain
Hint: For maximum array gain, use only the maximum
eigenchannel.
Where
Is the singular value decomposition (SVD) of H, and

12. Power-
Power-Bandwidth Trade-off
Trade-
The concept
Two basic definitions:
Spectral efficiency (SE): directly related to the channel capacity
in bit/s. This metric indicates how efficiently a limited frequency
spectrum is utilized. SE is quantified by: (in bit/s/Hz),
where R is the data rate and B is the channel bandwidth.
Energy Efficiency (EE): closely related to the power consumption
of the communication system. EE is usually quantified by the energy-
per-bit to noise power spectral density ratio, , where
(in Joules) and P is the signal power.
The efficiency of a communication system has traditionally been
measured in terms of SE and EE.

13. For any communication systems, it is desired to minimize the
consumed power, and minimize the required bandwidth as
well for a given R, or equivalently maximizing both SE and
EE.
However, this is not possible!
As a simple example, for AWGN channel, any achievable data
rate is upper bounded by
The power-bandwidth trade-off is commonly known
as EE-SE trade-off, where maximizing both EE and SE is
Equivalent to maximizing one and minimizing the other.

14. Power-
Power-Bandwidth Trade-off
Trade-
The concept
To mathematically formulate the EE-SE trade-off, lets follow the
following steps:
Via the Shannon’s capacity theorem, as far as the maximum
achievable SE, C, is concerned, it can be expressed as:
Where is the signal-to-noise ratio (SNR).
Without loss of generality,
Now, considering the achievable SE, , then can be
expresses as:

15. Power-
Power-Bandwidth Trade-off
Trade-
The concept
Then, by inserting (2) in (1), the EE-SE trade-off can be easily
expressed as:
Where is the inverse
function of f.
So, as indicated in (3), the problem of defining a closed-form
Expression for the EE-SE trade-off is generally equivalent to
obtaining an explicit expression for the inverse function of the
channel capacity per unit bandwidth,

16. Power-
Power-Bandwidth Trade-off
Trade-
Example: SISO AWGN-Channel
As a simple example, consider a simple additive white
Gaussian noise (AWGN) channel. In this case,
And hence, is directly given by
Substituting this formula in (3), and using C instead of S, EE-
SE trade-off for AWGN channel can be expressed as:

17. Power-
Power-Bandwidth Trade-off
Trade-
Example: SISO AWGN-Channel
12
10
Points above the curve satisfies
Shannon’s limit R < B log2 (1 + γ),
8 while the points below don’t
Eb /N0 (dB)
6
N
4
2
0
-2
-3 -2 -1 0 1
10 10 10 10 10
SpectralEf f iciency(bit/s/Hz)
Figure 1: EE-SE Trade-off for AWGN Channel

18. Power-
Power-Bandwidth Trade-off
Trade-
EE-SE Trade-off for MIMO System
In MIMO systems, the closed form of EE-SE trade-off is
more complicated since doesn’t have a straightforward
formulation. In this case, approximations of can
provide an acceptable solution.
As known, capacity expression for MIMO differs according
to the channel model used. In this presentation, the channel
is assumed to be a Rayleigh Fading channel with Gaussian
noise, which is a general case and other cases can be
considered as special cases.

19. EE- Trade-
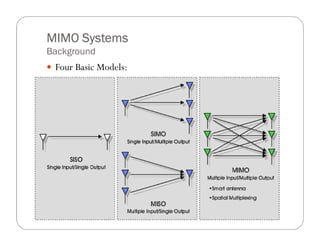
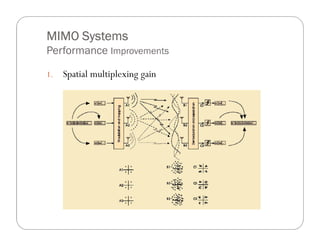
EE-ES Trade-off for MIMO Systems
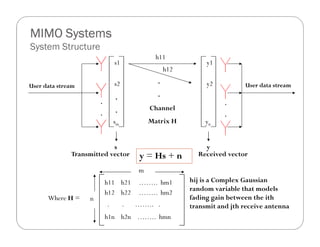
MIMO Capacity
Consider the MIMO-system model
y = Hx + n
With:
o The signal is transmitted over M transmit antennas
and received over N received antennas,
o , is a random matrix having independent and
identically distributed (i.i.d.) complex circular Gaussian
entries with zero-mean and unit variance.
o n: zero–mean complex Gaussian noise. Independent and
equal variance real and imaginary parts. E[nn†] = IN

20. EE- Trade-
EE-ES Trade-off for MIMO Systems
MIMO Capacity
o Also consider , where
is the total transmitted power.
o Then, the ergodic channel capacity per unit bandwidth of the
MIMO Rayleigh fading channel is accordingly expressed as:
H matrix is assumed to be unknown at the transmitter.
Considering the special case when the channel is a deterministic
Gaussian and H still Unknown at the transmitter, (4) can be
re-expressed as:

21. EE- Trade-
EE-ES Trade-off for MIMO Systems
MIMO Capacity
o Since it is not easy to find a closed-form for of (4),
two main approaches are usually used to plot EE-SE trade-off
curves,
Numerically, where different values for are computed
numerically for different SNR levels and corresponding Eb/No
values are also computed for those SNR values.
Approximated expressions for (4) are first introduced such
that the inverse can be computed and obtained in a closed-form
expression.
We will mention two of the research work done to obtain
approximated closed-form for the EE-SE.

22. EE- Trade-
EE-ES Trade-off for MIMO Systems
EE-SE Approximations - 1
o In [1], they approximated the EE-SE trade-off for the
situation of low SE and low EE.
o The approximated EE-SE trade-off is expressed as:
(5)
Where donates the minimum required for reliable
communication, and denotes the slope of spectral
efficiency in b/s/Hz/(3 dB) at the point

23. EE- Trade-
EE-ES Trade-off for MIMO Systems
EE-SE Approximations - 1
Where are the first and second derivatives of
, respectively.
For our assumed channel model,

24. EE- Trade-
EE-ES Trade-off for MIMO Systems
EE-SE Approximations - 2
o In [2], a closed-form approximation is provided for (4), as
follow:
Where
And is the ratio between receive and transmit
antennas
o This approximation was approved to have an acceptable
accuracy for M or N >2

25. EE- Trade-
EE-ES Trade-off for MIMO Systems
EE-SE Approximations - 2
o A simpler formulation can even be expressed as:
Where , and
o Solving this approximated expression to find its inverses, gave
the following solutions:
Case I: M=N, ,
Then:
(6)

26. EE- Trade-
EE-ES Trade-off for MIMO Systems
EE-SE Approximations - 2
Case II: M≠N, , then
(7)
Where: ,
and
are values depending on the value of (see table I
in [2])

27. EE- Trade-
EE-ES Trade-off for MIMO Systems
EE-SE Approximations - 2
In (6) and (7), is the real branch of the Lambert W function
which is the inverse of the function and thus it
satisfies , and then,

28. EE- Trade-
EE-ES Trade-off for MIMO Systems
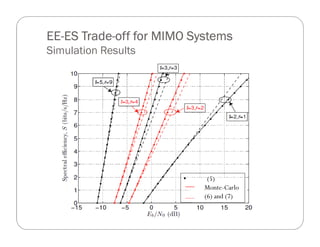
Simulation Results
The following simulation result presented in [2], where the EE-
SE trade-offs is plotted for three methods:
Numerical computation: as mentioned previously using Monte
Carlo simulation to get the inverse of (4).
Using approximation-1 as described in (5), and detailed in [1].
Using approximation-2 as described in (6) and (7) and detailed
in [2].
Results are simulated for different number of transmit (t) and
receive (r) antennas.

29. EE- Trade-
EE-ES Trade-off for MIMO Systems
Simulation Results
• (5)
Monte-Carlo
(6) and (7)

30. EE- Trade-
EE-ES Trade-off for MIMO Systems
Discussion
Simulation results show a good fit between the exact expression
in (4) and the approximated ones in (6) and (7) for wide range of
SE and different values of transmit and receive antennas, while
the fit is not that accurate with the approximated expression in
(5) when the SE is getting higher specially for small number of
transmit and receive antennas.

31. Conclusions
The use of MIMO systems is a powerful performance enhancing
technology.
Energy efficiency (EE) and spectral efficiency (SE) are
important metrics in evaluation the performance of the
communication systems, where they are better to be maximized.
However, maximizing energy efficiency EE while maximizing
the SE is a conflicting object, the concept of power-bandwidth
trade-off!
Some works have been done to formulate the SE-EE trade-off
for MIMO systems.

32. References
[1] S. Verdu, "Spectral efficiency in the wideband regime", IEEE Trans. Inf. Theory,,
vol. 48, no. 6, pp. 13191343, June 2002
[2] F. Hliot, M. Imran, and R. Tafazolli, "On the Energy efficiency -Spectral efficiency
Trade-o over the MIMO Rayleigh Fading Channel“ ,IEEE Trans. Communications,
VOL. 60, NO. 5, MAY 2012.
[3] I. E. Telatar, "Capacity of multi-antenna Gaussian channels“ ,Europe. Trans.
Telecomm. Related Techno, vol. 10, no. 6, pp. 585596, Nov. 1999.
[4] F. Hliot, M. Imran, and R. Tafazolli, "An accurate closed-form approximation of
the energy efficiency -spectral efficiency trade-o over the MIMO Rayleigh fading
channel“ ,in Proc. 2011 IEEE ICC, 4th Int. Workshop Green Comm..,
[5] O. Oyman and A. J. Paulraj, "Spectral efficiency of relay networks in the power
limited regime",in Proc. 2004 Allerton Conf. Commun., Control Computing.
[6] S. de la Kethulle, "An Overview of MIMO Systems in Wireless
communications," Lecture in Communication Theory for Wireless Channels,
September 27, 2004.