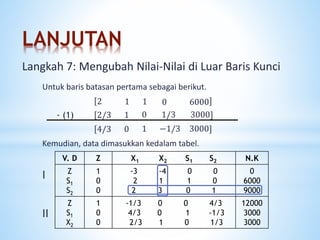
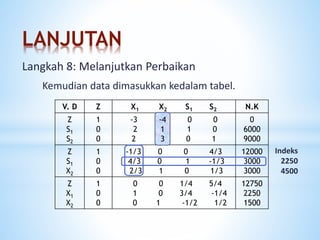
Dokumen ini membahas metode simpleks dalam program linier untuk pengambilan keputusan optimal terkait pengalokasian sumberdaya. Metode ini diperkenalkan oleh George B. Dantzig pada tahun 1950 dan melibatkan prosedur iteratif untuk mencapai solusi optimal melalui langkah-langkah sistematis. Terdapat langkah-langkah detail yang harus diikuti untuk menyusun tabel dan memilih kolom serta baris kunci dalam proses penyelesaian masalah.

1. NAMA : HAZHIYAH RAMADHANI
NIM : 14.01.0046/M
KELAS : K-01
METODE SIMPLEKS

2. PENDAHULUAN
Metode simpleks merupakan salah satu teknik
penyelesaian dalam program linier yang
digunakan sebagai teknik pengambilan keputusan
dalam permasalahan yang berhubungan
dengan pengalokasian sumberdaya secara
optimal.
Metode simpleks digunakan untuk mencari nilai
optimal dari program linier yang melibatkan
banyak constraint (pembatas) dan banyak variabel
(lebih dari dua variabel).

3. LANJUTAN
Metode Simpleks pertama sekali diperkenalkan oleh
George B.Dantzig dari USA (1950) melalui bukunya
Linear Programming and Extension, menyebutkan
bahwa ide dari linear programming ini berasal dari
ahli matematika Rusia bernama L.V
Kantorivich. Akan tetapi ide ini rupanya di Rusia
tidak bisa berkembang. Malah ternyata dunia barat
yang memanfaatkan ide ini selanjutnya.

4. LANJUTAN
Metode Simpleks merupakan prosedur aljabar yang
bersifat iteratif yang bergerak selangkah demi
selangkah, dimulai dari suatu titik ekstrem pada
daerah fisibel (ruang solusi) menuju ke titik ekstrem
yang optimum.
Metode simpleks akan sangat efektif digunakan untuk
persoalan program linear dengan lebih dari dua
variabel keputusan, dalam hal ini bukan berarti
metode simpleks tidak dapat digunakan untuk
menyelesaikan persoalan dengan dua variabel
keputusan.

5. LANGKAH-LANGKAH
METODE SIMPLEKS
Langkah-langkah awal dalam pemecahan masalah, yaitu formula
masalahnya sama yang dilakukan pada metode grafik, misalnya
contoh pada PT Kembang Arum di depan, yang formulasinya sebagai
berikut:
Fungsi tujuan: maksimumkan Z= 3X1 + 4X2
Batasan-batasan :
1. 2X1 + X2 ≤ 6000
2. 2X1 + 3X2 ≤ 9000
3. X1 ≥ 0; X2 ≥ 0

6. LANJUTAN
Langkah 1: Mengubah Fungsi Tujuan
Fungsi tujuan diubah sedemikian sehingga
semua variabel yang belum diketahui nilainya
berada disebelah kiri tanda sama dengan (=),
fungsi tujuan :
Maksimumkan Z= 3X1 + 4X2 diubah
menjadi:
Maksimumkan Z - 3X1 - 4X2

7. LANJUTAN
Langkah 2: Mengubah Batasan-Batasan
Semua batasan yang mula-mula bertanda ≤ diubah menjadi =,
dengan menggunakan suatu tambahan variabel yang sering
disebut sebagai slack variable dan biasanya diberi simbol S.
Batasan 1: 2X1 + X2 ≤ 6000 diubah menjadi: 2X1 + X2 + S1 = 6000
Batasan 2: 2X1 + 3X2 ≤ 9000 diubah menjadi: 2X1 + 3X2 + S2 =
9000
Dengan demikian, bentuk persamaan-persamaan tadi menjadi
sebagai berikut:
Fungsi tujuan: maksimumkan Z – 3X1 – 4X2 = 0
Batasan-batasan: 1. 2X1 + X2 + S1 = 6000
2. 2X1 + 3X2 + S2 = 9000
3. X1, X2, S1, S2 ≥ 0

8. Langkah 3: Menyusun Persamaan-persamaan ke Dalam Tabel
Dalam setiap atabel simpleks harus diperhatikan bahwa
nilai variabel dasar pada baris Z harus 0. dapat dilihat
bahwa nilai S1 dan S2 pada baris Z adalah 0. Kalau nilai
variabel dasar itu tidak 0 maka tabel tidak bisa diselesaikan
dengan linear programming, mungkin terdapat kesalahan
pada dalam langkah sebelumnya. isamping itu, perlu
diperhatikan pula bahwa nilai kanan pada baris batasan
harus selalu positif.
V. D Z X1 X2 S1 S2 N.K
Z 1 -3 -4 0 0 0
S1 0 2 1 1 0 6000
S2 0 2 3 0 1 9000
LANJUTAN

9. LANJUTAN
Kolom kunci merupakan dasar untuk mengubah/
memperbaiki tabel sebelumnya. Agar lebih cepat
memperoleh pemecahan optimal, pilihlah kolom pada
baris Z mempunyai nilai paling negatif.
Selama dalam baris Z masih terdapat bilangan negatif
maka tabel itu masih bisa diubah/ diperbaiki, tetapi
kalau sudah tidak ada negatif berarti tabel sudah
optimal.
Langkah 4: Memilih Kolom Kunci
V. D Z X1 X2 S1 S2 N.K
1
0
0
-3 -4 0 0
2 1 1 0
2 3 0 1
0
6000
9000

10. LANJUTAN
Baris kunci adalah baris yang merupakan dasar untuk
mengubah/ mengadakan perbaikan. Untuk
menentukannya terlebih dahulu harus dicari indeks
tiap-tiap baris dengan cara sebagai berikut.
Indeks baris =
Nilai pada kolom N.K
Nilai pada kolom kunci
Pada baris pertama nilai pada kolom N.K sebesar 6000
dan nilai pada kolom kunci = 1. jadi indeksnya 6000/1
= 6000. Sedang untuk baris batasan ke-2 nilai kolom
kunci 3 sehingga indeksnya 9000/3 = 3000.
Langkah 5: Memilih Baris Kunci

11. LANJUTAN
Kemudian kita pilih baris kunci yang memiliki
indeks positif terkecil, yaitu baris batasan kedua
(indeks batasan pertama 6000 dan batasan kedua
hanya 3000.
Langkah 5: Memilih Baris Kunci
V. D Z X1 X2 S1 S2 N.K
Z
S1
S2
1
0
0
-3 -4 0 0
2 1 1 0
2 3 0 1
0
6000
9000

12. LANJUTAN
Mula-mula yang diubah ialah baris kunci dengan
membagi semua angkanya dengan angka kunci.
Jadi semua angka pada baris kunci dibagi 3.
I
II
Langkah 6: Mengubah Nilai Baris Kunci
V. D Z X1 X2 S1 S2 N.K
Z
S1
S2
1
0
0
-3 -4 0 0
2 1 1 0
2 3 0 1
0
6000
9000
Z
S1
X2
1
0
0 2/3 1 0 1/3 3000

13. LANJUTAN
Nilai baru dari baris-baris yang bukan merupakan
baris kunci dapat dihitung dengan rumus sebagai
berikut.
Nilai
baris
baru
=
Nilai
baris
lama
−
Koefisien
pada
kolom kunci
×
Nilai
baris
kunci
Untuk baris Z pada tabel dapat dihitung sebagai
berikut.
−3 −4 0 0 0
- (-4) 2
3 1 0 1
3 3000
−1
3 0 0 4
3 12000
Langkah 7: Mengubah Nilai-Nilai di Luar Baris Kunci

14. LANJUTAN
Untuk baris batasan pertama sebagai berikut.
2 1 1 0 6000
- (1) 2/3 1 0 1/3 3000
4/3 0 1 −1/3 3000
Kemudian, data dimasukkan kedalam tabel.
I
II
Langkah 7: Mengubah Nilai-Nilai di Luar Baris Kunci
V. D Z X1 X2 S1 S2 N.K
Z
S1
S2
1
0
0
-3 -4 0 0
2 1 1 0
2 3 0 1
0
6000
9000
Z
S1
X2
1
0
0
-1/3 0 0 4/3
4/3 0 1 -1/3
2/3 1 0 1/3
12000
3000
3000

15. LANJUTAN
Selama masih ada nilai negatif pada baris Z, ulangilah
langkah perbaikan mulai dari langkah 3 sampai langkah
7 sampai diperoleh pemecahan optimal. Kalau sudah
tidak ada nilai negatif pada baris Z berarti alokasi sudah
optimal. Kalau tabel dilangkah 7 diubah lagi, maka yang
menjadi kolom kunci adalah X1 dan yang terpilih sebagai
baris kunci adalah barisan pertama (S1). Dengan angka
kunci 4/3, semua angka pada baris batasan pertama
dibagi 4/3 dan hasilnya sebagai berikut.
1 0 ¾ - ¼ 2250
Langkah 8: Melanjutkan Perbaikan

16. LANJUTAN
Nilai baru dari baris Z menjadi:
−1
3 0 1 4
3 12000
- (-1/3) 1 0 3
4
−1
4 2250
0 0 1
4
5
4 12750
Untuk baris batasan pertama sebagai berikut.
2
3 1 0 1
3 3000
- (2/3) 1 0 3
4
−1
4 2250
0 1 −1
2
1
2 1500
Langkah 8: Melanjutkan Perbaikan

17. LANJUTAN
Kemudian data dimasukkan kedalam tabel.
Indeks
2250
4500
Langkah 8: Melanjutkan Perbaikan
V. D Z X1 X2 S1 S2 N.K
Z
S1
S2
1
0
0
-3 -4 0 0
2 1 1 0
2 3 0 1
0
6000
9000
Z
S1
X2
1
0
0
-1/3 0 0 4/3
4/3 0 1 -1/3
2/3 1 0 1/3
12000
3000
3000
Z
X1
X2
1
0
0
0 0 1/4 5/4
1 0 3/4 -1/4
0 1 -1/2 1/2
12750
2250
1500
-4
1
3

18. PENYIMPANGAN-PENYIMPANGAN DARI BENTUK
STANDAR
1. Fungsi Tujuan Bersifat Meminimumkan Nilai Z
Kalau fungsi tujuan meminimumkan nilai Z maka harus
diubah menjadi memaksimumkan . Untuk mengubahnya
dapat dilakukan dengan mengalikannya dengan -1. Jadi,
meminimumkan nilai positifnya sama dengan
memaksimumkan nilai negatifnya.
2. Batasan Bertanda Sama Dengan (=)
Kalau suatu batasan bertanda sama dengan maka kalau
langsung dimasukkan dalam tabel akan mengalami
kesulitan karena variabel tersebut memiliki variabel dasar.
Oleh karena itu harus diberi tambahan suatu variabel yaitu
artificial variable yang biasanya diberi simbol R.

19. PENYIMPANGAN-PENYIMPANGAN DARI BENTUK
STANDAR
3. Batasan dengan Tanda Lebih Besar Sama Dengan (≥)
kalau suatu batasan bertanda ≥ maka kita beri Slack
variable yang bertanda negatif karena kelebihan dibagian
kiri tanda persamaan ditampung dalam-S sehingga bisa
menjadi persamaan, tetapi kalalu –S di jadikan variabel
dasar maka akan terdapat suatu variabel yang bernilai
negatif, yaitu variabel S. Hal ini melanggar non-variabel,
yaitu variabel R.