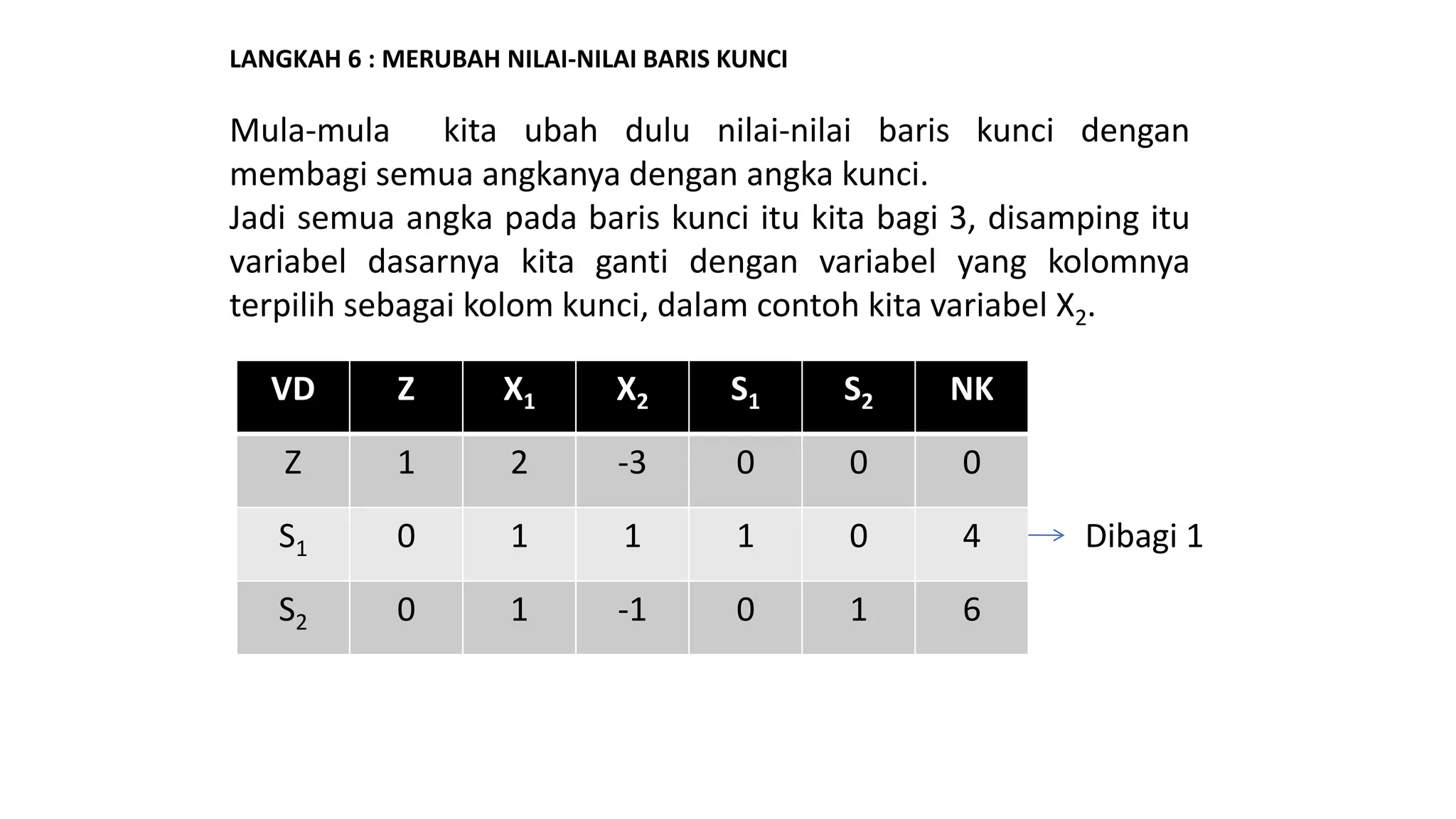
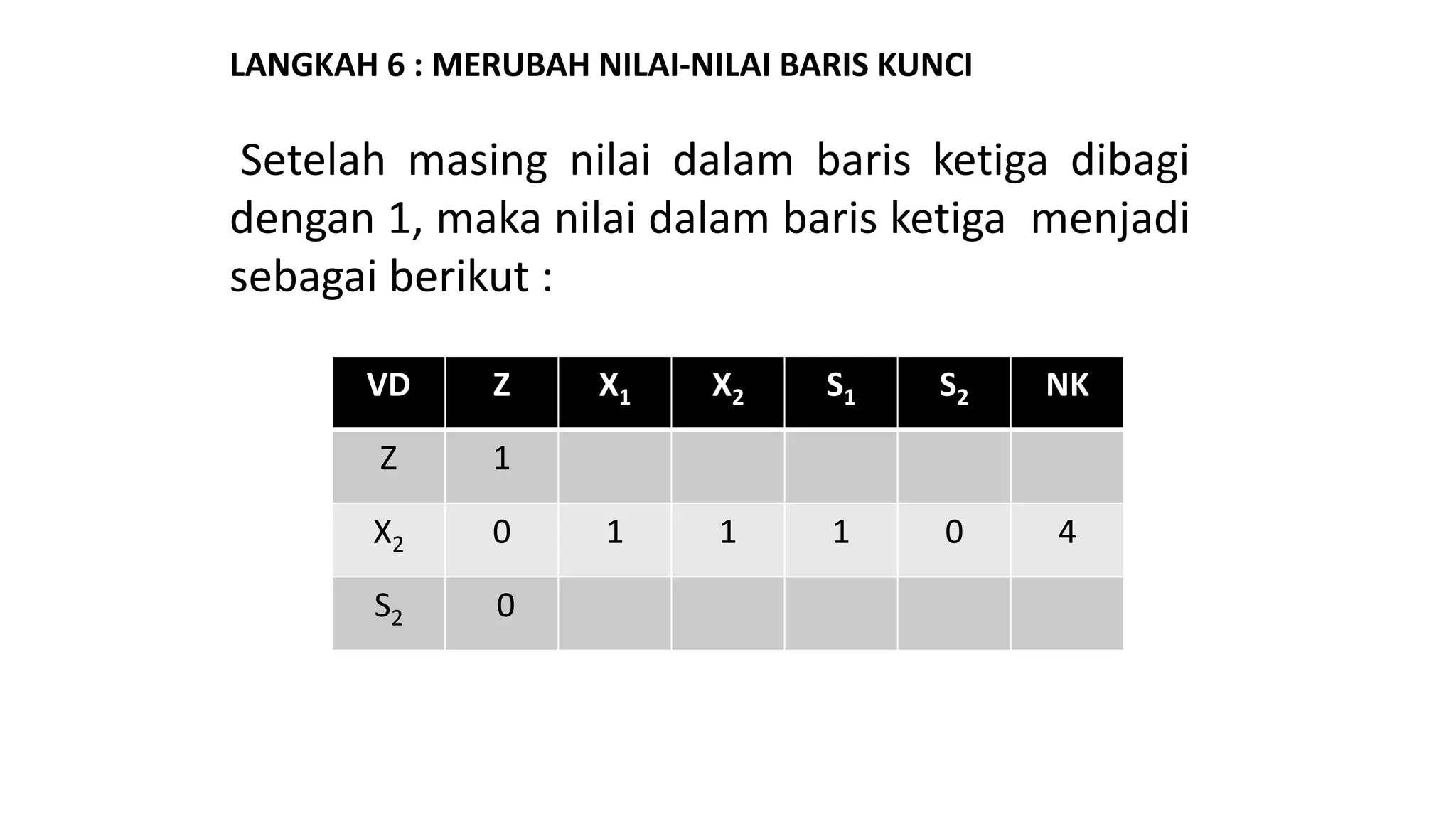
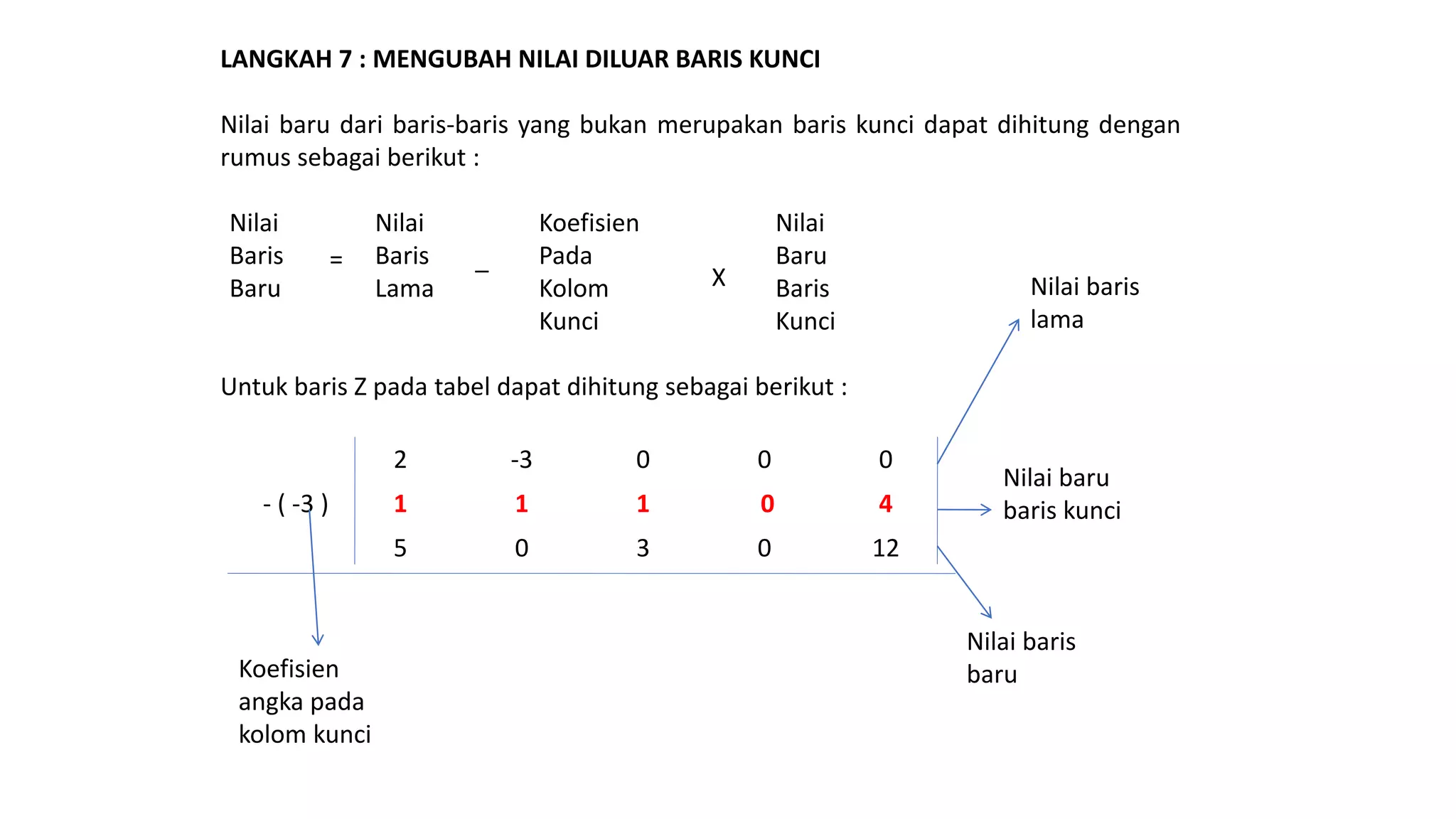
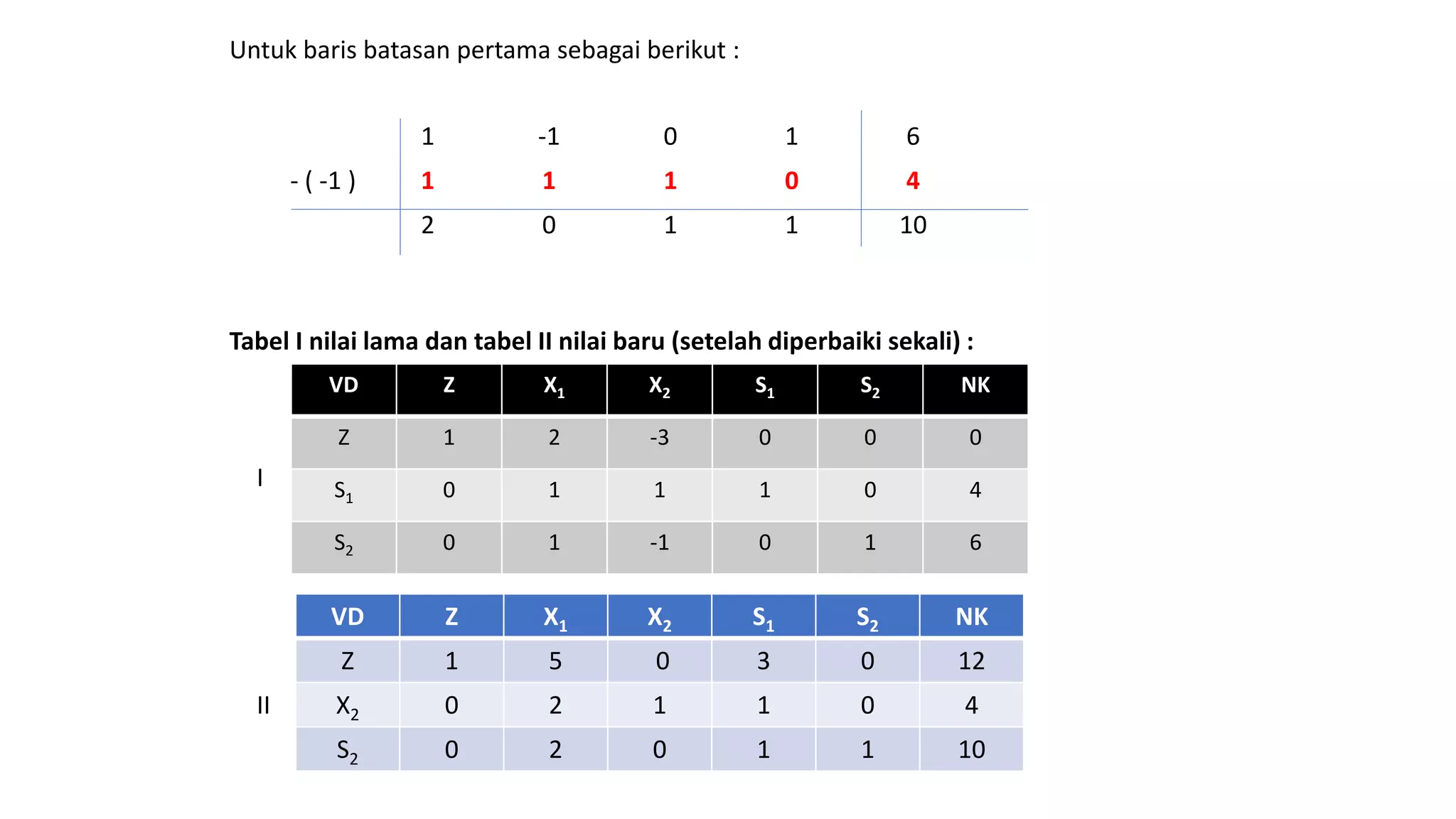
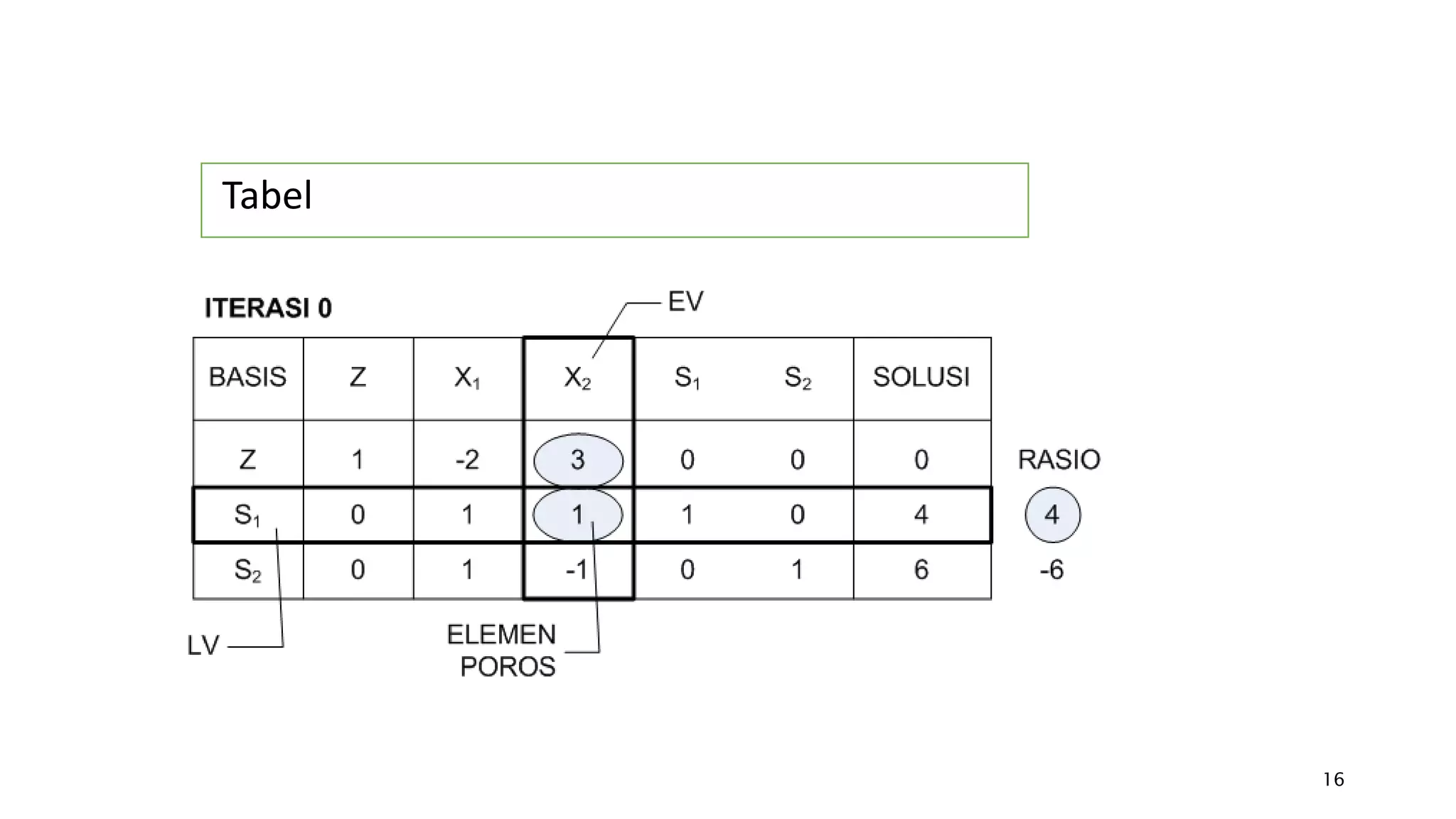
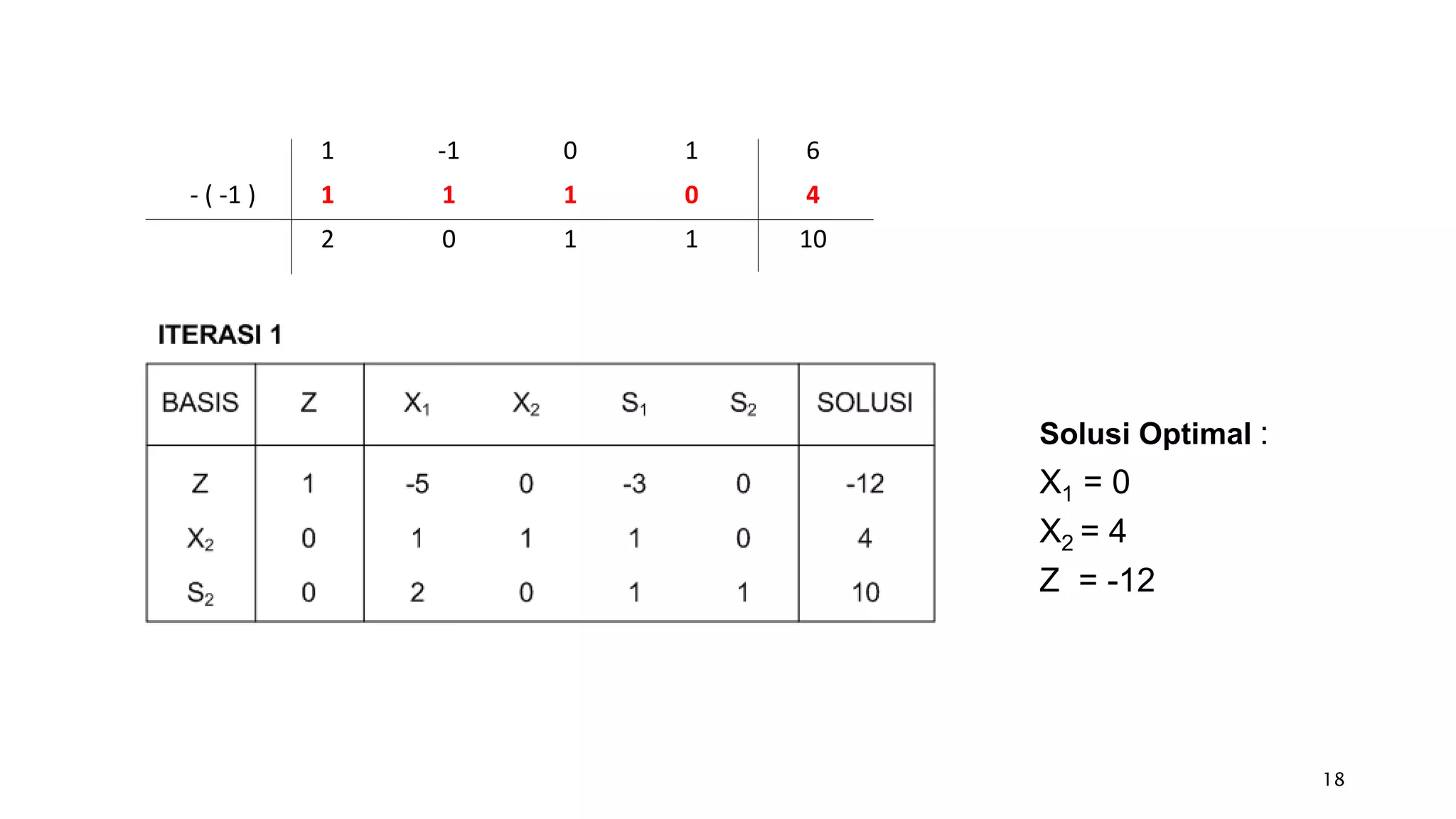
Dokumen tersebut membahas tentang penyelesaian permasalahan program linear dengan fungsi tujuan minimisasi menggunakan metode simpleks. Ada dua metode yang dibahas, yaitu dengan merubah fungsi tujuan menjadi maksimisasi atau tetap mempertahankan fungsi tujuan minimisasi asli. Metode kedua dipilih dengan memilih variabel yang koefisiennya paling positif sebagai kolom kunci.

1. LINEAR PROGRAMMING : METODE SIMPLEKS
PERMASALAHAN MINIMISASI
• Prosedur dalam penyelesaian permasalahan maksimisasi dapat juga
kita gunakan untuk menyelesaikan permasalahan minimisasi yang
biasanya mempunyai tanda dan atau = pada fungsi kendalanya.
• Pada topik ini akan kita bahas mengenai penyelesaian permasalahan
LP dengan fungsi tujuan minimisasi.
• Pada permasalahan minimisasi, biasanya kita jumpai tanda ≥ pada
fungsi kendala. Kendati demikian tidak menutup kemungkinan fungsi
kendala mempunyai tanda =.

2. Ada 2 Metode dalam penyelesaikan kasus minimisasi
Metode 1.
Sama hal dengan penyelesaian maksimisasi Meminimumkan nilai Z
sama dengan memaksimumkan Nila –Z
Metode 2.
Tidak perlu merubah fungsi tujuan Z.
Untuk m emilih koom kunci, dengan cara memilih unsur dalam baris Z
yang nilainya paling positif. Solusi optimum dicapai apabila dalam baris
Z semua unsur sudah bernilai Non positif semua.

3. Metode 1.
Sama hal dengan penyelesaian maksimisasi Meminimumkan nilai Z
sama dengan memaksimumkan Nila –Z
Metode 2.
Tidak perlu merubah fungsi tujuan Z.
Untuk m emilih koom kunci, dengan cara memilih unsur dalam baris Z
yang nilainya paling positif. Solusi optimum dicapai apabila dalam baris
Z semua unsur sudah bernilai Non positif semua.

4. F. Tujuan : min Z = 2X1 - 3X2
F. Pembatas :
X1 + X2 ≤ 4
X1 - X2 ≤ 6
X1 , X2 ≥ 0
Penyelesaian dengan metode 1.
F. Tujuan : min Z = 2X1 - 3X2
max - Z = - 2X1 + 3X2
F. Pembatas :
X1 + X2 + S1 = 4
X1 - X2 + S2 = 6
X1 , X2 , S1 , S2 ≥ 0
4
Contoh Dengan Simpleks Biasa

5. F. Tujuan : min Z = 2X1 - 3X2
F. Pembatas :
X1 + X2 ≤ 4
X1 - X2 ≤ 6
X1 , X2 ≥ 0
Konversi ke dalam bentuk standar/kanonik
F. Tujuan : min Z = 2X1 - 3X2 + 0S1 + 0S2
- Z = - 2X1 + 3X2 - 0S1 - 0S2
- Z + 2X1 - 3X2 + 0S1 + 0S2 = 0
F. Pembatas :
X1 + X2 + S1 = 4
X1 - X2 + S2 = 6
X1 , X2 , S1 , S2 ≥ 0
5
Contoh Dengan Simpleks Biasa

6. LANGKAH 3 : MENYUSUN PERSAMAAN KE DALAM TABEL
LANGKAH 4 : MEMILIH KOLOM KUNCI
Pilih kolom yang pada garis Z mempunyai nilai
negatif terkecil (pailng negatif).
VD -Z X1 X2 S1 S2 NK
Z 1 2 -3 0 0 0
S1 0 1 1 1 0 4
S2 0 1 -1 0 1 6
Kolom kunci
Baris kunci
Angka kunci

7. LANGKAH 5 : MEMILIH BARIS KUNCI
baris kunci adalah baris yang merupakan dasar untuk
mengubah / mengadakan perbaikan. Untuk
menentukannya terlebih dahulu harus kita cari indeks
tiap-tiap baris dengan cara sebagai berikut :
kunci
kolom
pada
nilai
NK
kolom
pada
nilai
baris
indeks 

8. LANGKAH 5 : MEMILIH BARIS KUNCI :
Indeks : 4 / 1 = 4
6 / -1 = -6  diabaikan
Kemudian kita pilih baris kunci, yaitu baris yang mempunyai
indeks positif terkecil, yaitu baris batasan kedua (indeks
batasan pertama 4 dan batasan kedua hanya -6). Kemudian
baris kunci ini kita beri tanda (dilingkari) agar lebih mudah
mengingatnya. Kita lihat ada angka yang masuk dalam kolom
kunci dan juga masuk dalam baris kunci disebut angka kunci
sebesar 1.

9. LANGKAH 6 : MERUBAH NILAI-NILAI BARIS KUNCI
Mula-mula kita ubah dulu nilai-nilai baris kunci dengan
membagi semua angkanya dengan angka kunci.
Jadi semua angka pada baris kunci itu kita bagi 3, disamping itu
variabel dasarnya kita ganti dengan variabel yang kolomnya
terpilih sebagai kolom kunci, dalam contoh kita variabel X2.
VD Z X1 X2 S1 S2 NK
Z 1 2 -3 0 0 0
S1 0 1 1 1 0 4
S2 0 1 -1 0 1 6
Dibagi 1

10. LANGKAH 6 : MERUBAH NILAI-NILAI BARIS KUNCI
Setelah masing nilai dalam baris ketiga dibagi
dengan 1, maka nilai dalam baris ketiga menjadi
sebagai berikut :
VD Z X1 X2 S1 S2 NK
Z 1
X2 0 1 1 1 0 4
S2 0

11. LANGKAH 7 : MENGUBAH NILAI DILUAR BARIS KUNCI
Nilai baru dari baris-baris yang bukan merupakan baris
kunci dapat dihitung dengan rumus sebagai berikut :
Nilai Baris
Baru =
Nilai Baris
Lama
Koefisien Pada
Kolom Kunci
Nilai Baru
Baris Kunci
X
_

12. LANGKAH 7 : MENGUBAH NILAI DILUAR BARIS KUNCI
Nilai baru dari baris-baris yang bukan merupakan baris kunci dapat dihitung dengan
rumus sebagai berikut :
Untuk baris Z pada tabel dapat dihitung sebagai berikut :
Nilai
Baris
Baru
=
Nilai
Baris
Lama
Koefisien
Pada
Kolom
Kunci
Nilai
Baru
Baris
Kunci
X
_
2 -3 0 0 0
- ( -3 ) 1 1 1 0 4
5 0 3 0 12
Nilai baru
baris kunci
Koefisien
angka pada
kolom kunci
Nilai baris
lama
Nilai baris
baru

13. Untuk baris batasan pertama sebagai berikut :
Tabel I nilai lama dan tabel II nilai baru (setelah diperbaiki sekali) :
VD Z X1 X2 S1 S2 NK
Z 1 5 0 3 0 12
X2 0 2 1 1 0 4
S2 0 2 0 1 1 10
I
II
1 -1 0 1 6
- ( -1 ) 1 1 1 0 4
2 0 1 1 10
VD Z X1 X2 S1 S2 NK
Z 1 2 -3 0 0 0
S1 0 1 1 1 0 4
S2 0 1 -1 0 1 6

14. Pada bagian III dari tabel di atas ternyata dalam bari Z sudah
tidak memiliki negatif lagi, berarti tabel ini sudah optimal.
Arti dari hasil pemecahan optimal ini sebagai berikut :
Produk a dihasilkan 4 (X2 = 4)
Produk kedua dihasilkan 6 unit (s2 = 6)
Sumbangan terhadap penurunan sebesar Rp. 12
(Z = 12.)

15. 15
Metode 2
Untuk menentukan kolom kunci dicari angka baris Z yang paling
positif, dalam hal ini adalah 3 pada X2
F. Tujuan : min Z = 2X1 - 3X2
F. Pembatas :
X1 + X2 ≤ 4
X1 - X2 ≤ 6
X1 , X2 ≥ 0
Merubah dalam bentuk kanonik
Z - 2X1 + 3X2 - 0S1 - 0S2 = 0
X1 + X2 + S1 = 4
X1 - X2 + S2 = 6

16. 16
Tabel

17. 17
Solusi Optimal :
X1 = 0
X2 = 4
Z = -12
-2 3 0 0 0
- ( 3 ) 1 1 1 0 4
-5 0 -3 0 -12

18. 18
Solusi Optimal :
X1 = 0
X2 = 4
Z = -12
1 -1 0 1 6
- ( -1 ) 1 1 1 0 4
2 0 1 1 10

19. 19
Solusi Optimal :
X1 = 0
X2 = 4
Z = -12