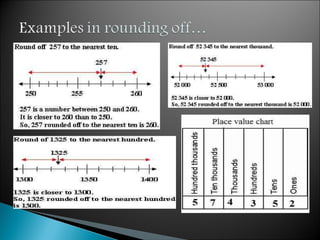
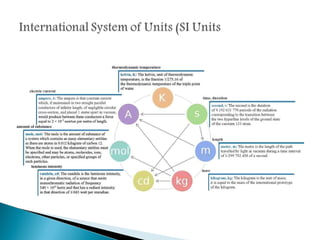
Measurement is the basis of all scientific work, as there are standardized units to quantify different properties like length, mass, time, and others. Various methods like dimensional analysis and factor-label simplify conversions between units by treating them as numbers that can be multiplied or divided. Understanding significant figures and rounding properly is also important when making measurements and calculations in science.

1. By
Prof. Liwayway Memije-Cruz
Measurement: The basis
of all scientific work

2. Measurement is the process of finding out how many
units there are in something. The basis of all scientific
work is measurement. There are various units of
measurement depending on what we wish to
measure. There are measurements of length, mass,
force, volume, time, velocity, density, electric current
and many others and these are expressed in different
units.
Almost all of us use measurements. The food we eat,
the clothes and shoes we wear, the work we do, and
many of the games we play involve measurements.

5. Using the dimensional analysis or factor-label method simplifies the conversion between various units. If units are treated
like numbers, they can be multiplied, divide or cancelled. A conversion factor which is written in the form of ratio is used
to change the units given in the data to the units asked for in the answer. given quantity x conversion factor = desired
quantity
Examples:
1. Convert 8.0 inches to cm
Given: 8.0 inches Conversion factor: 1 inch = 2.54cm
Solution:
8.0 in x 2.54 cm = 20.32 cm
1 inch
2. Convert 15cm to km
Given: 15 cm Conversion factors:
1m---__
102
cm
1km-_
103
m
Solution:
15cm x 1m---_ x 1km-_ = 15/105
km or
102
cm 103
m 15 x 10-5
km

6.  How many inches are there in 13 centimeters?
Conversion factor: 1 cm = 0.39.37
15 cm x 0.3937in/cm = 5.9055 in
Complete the following:
a. 13g = ___________ kg
b. 3451 mg = ________ g
c. 4.18 g = __________mg
d. 17.38 km = _______ cm

7. where M is the number between 0 and 10 and
n is a positive or negative integer. n is the
exponent or power of the number. It
expresses the number of times 10 is
multiplied by it.
Rules in writing a number in scientific notation:
 Retain one digit before the decimal point.
 Multiply M by 10 raised to the proper value
of n, where n is equal to the number of
decimal places the point is moved.
 Positive exponent means the decimal point
was moved to the left.
 Negative exponent means the decimal point
was moved to the right.
Scientific notation has the form M x 10n

8.  Significant figures are numbers that are either certain or good
estimates of numbers. All numbers greater than zero are significant.
A zero, which is part of a measurement, is significant. A zero used
just to locate a decimal point is not significant.

9.  If the figure to be dropped is greater than 5,
increase by one the value of the last figure to be
retained.
 If the figure to be dropped is less than 5, the last
figure to be retained should not be changed.
 If the number to be dropped is 5, the last figure to
be retained is increased by one if it odd, and
retained as is, if it is even.

12. Indicate the SI base units appropriate to express the following:
 length of a 100 mile race = kilometer
 mass of the horse = kilogram
 volume of a swimming pool = cubic meter
 speed of a racing car = kilometer per hour
 density of metallic gold = grams per cubic centimeter
 area of a basketball court = square meters
 the maximum temperature at the North pole on April 1, 1913 =
Kelvin

14. Laboratory experiments require measurements of length, mass, volume,
and temperature. Meter is the unit of length. Kilogram is the unit of
mass. Second is the unit of time. Kelvin is the unit of thermodynamic
temperature. The natural unit of capacity is based on a standard unit of
length. Volume is length cubed (P). The most common unit of volume
used in chemistry is the liter. Density is the mass or quantity of matter of
a substance contained in one unit of its volume.
 Density = mass per unit volume = mass of body/volume of body
 Specific gravity (Relative Density) = mass of solid or liquid/mass of an
equal volume of water

15. Temperature is a measure of how hot something is. It is usually measured with a
thermometer has a scale that gives an amount of hotness a certain number value.
There are two common scales of temperature, the Fahrenheit scale and the
Celsius scale. Extremely high temperature may be measured with a pyrometer.
Aside from showing how hot an object is, temperature is a measure of the kinetic
energy (energy of motion) of molecules that make up an object. When energy is
added to an object, the additional energy usually increases the kinetic energy of
the molecules and the object gets hotter. For example, energy is added to a gas as
it is squeezed, to a liquid as it is stirred, and to a solid as it is hammered. A
thermometer shows this increase in energy as a rise in temperature.
Formulas used in the inter conversions of the scales:
◦ ºC = 5/9 (ºF – 32)
◦ ºF = 9/5 ºC + 32
◦ K = ºC + 273

16. 1. Normal body temperature is 98.6 ºF. What is the
temperature in degrees Celsius and Kelvin?
Conversion Factors: ºC = 5/9 (ºF – 32)
ºK = ºC + 273
ºC = 5/9 (98.6 – 32) = 5/9 (66.6) = 37.0 ºC
ºK = 37.0 + 273 = 310ºK
2. Convert 30 ºC to ºF.
Conversion Factor: ºF = 9/5 ºC + 32
ºF = 9x30/5 + 32 = 86ºF

17. Chemical knowledge is obtained fundamentally by careful
observation of the behavior of nature.
Scientific method of approaching problems:
Careful observation = Persistent search for truth =
Intelligence thought = Progress