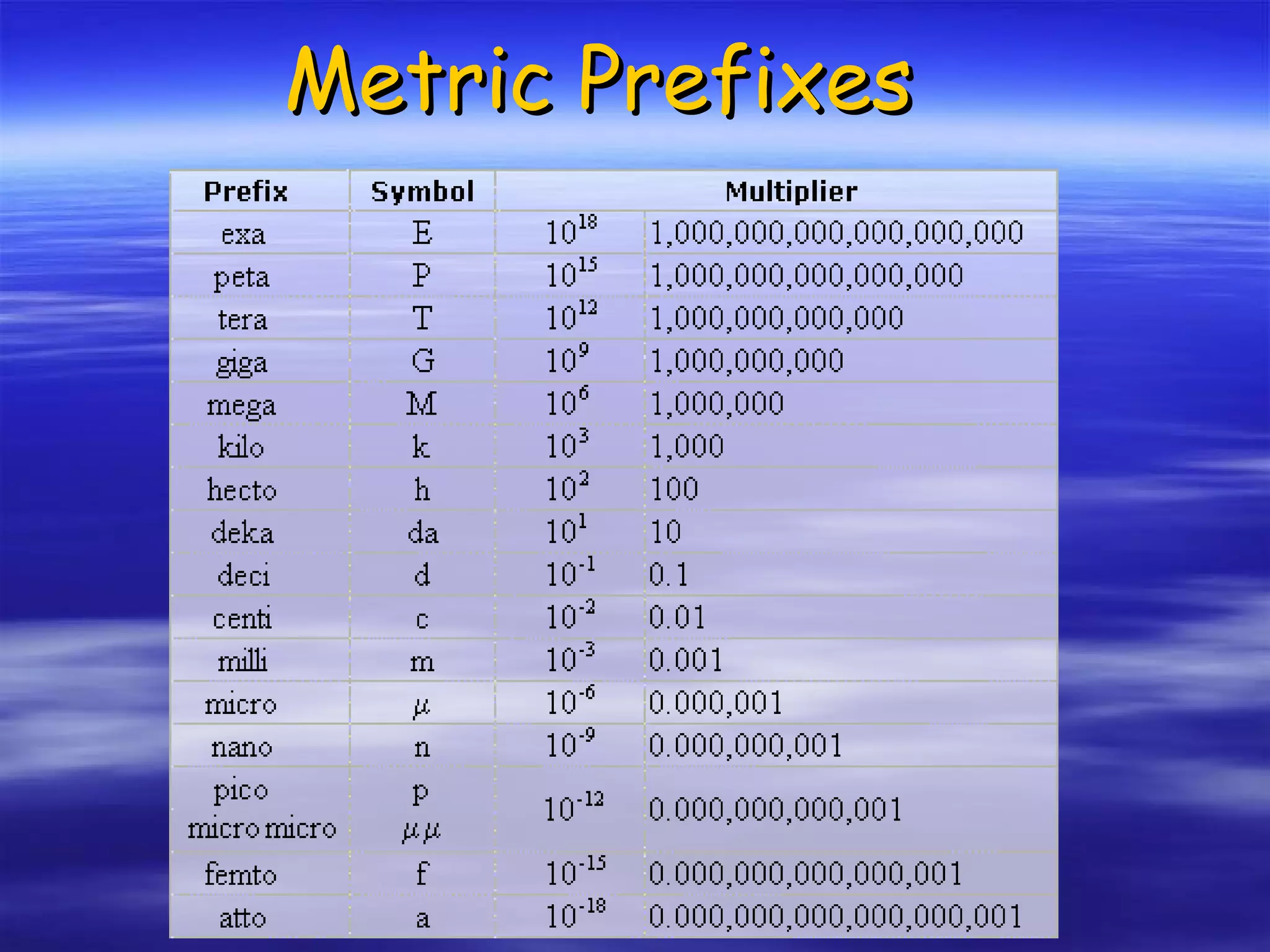
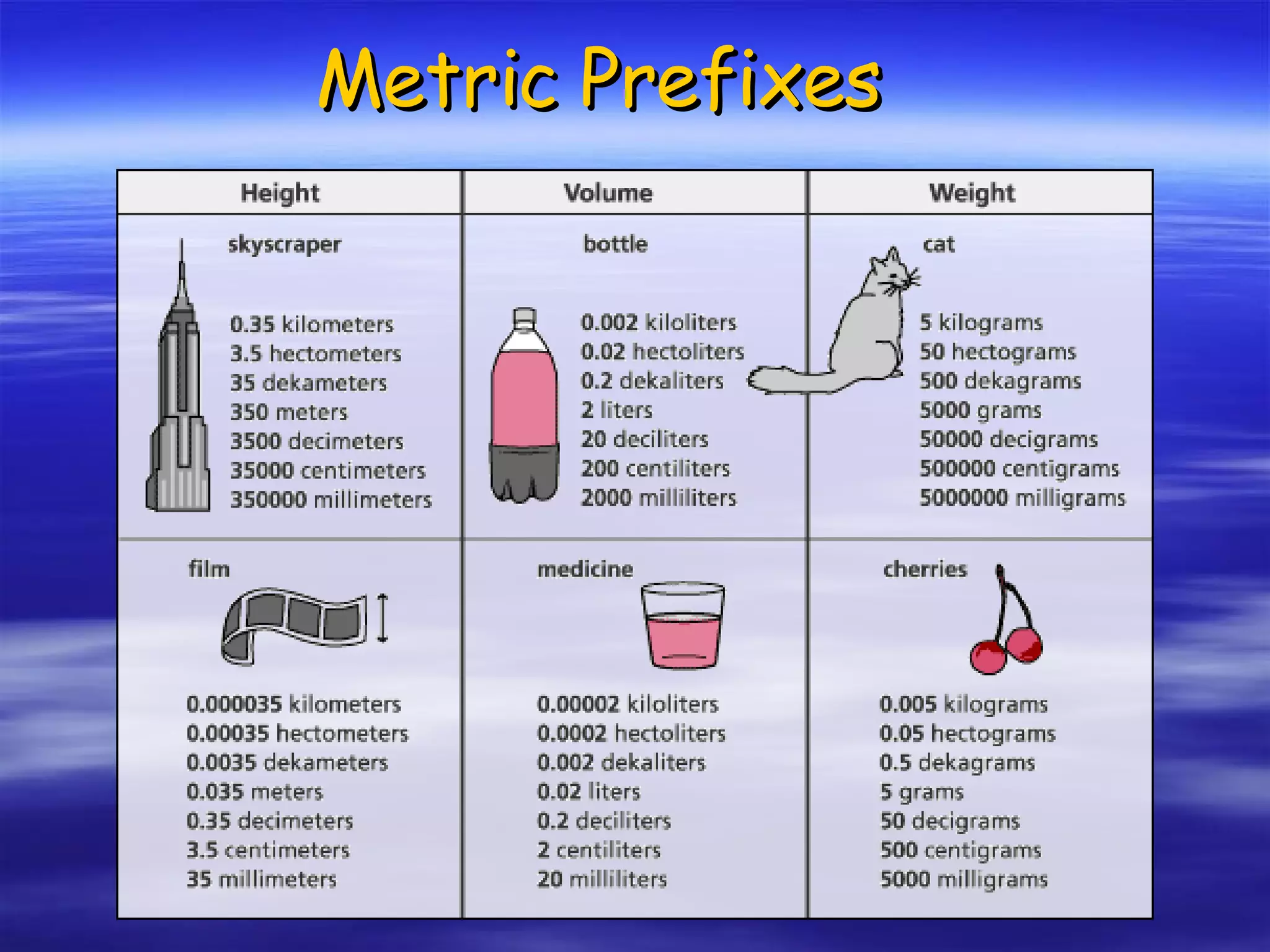
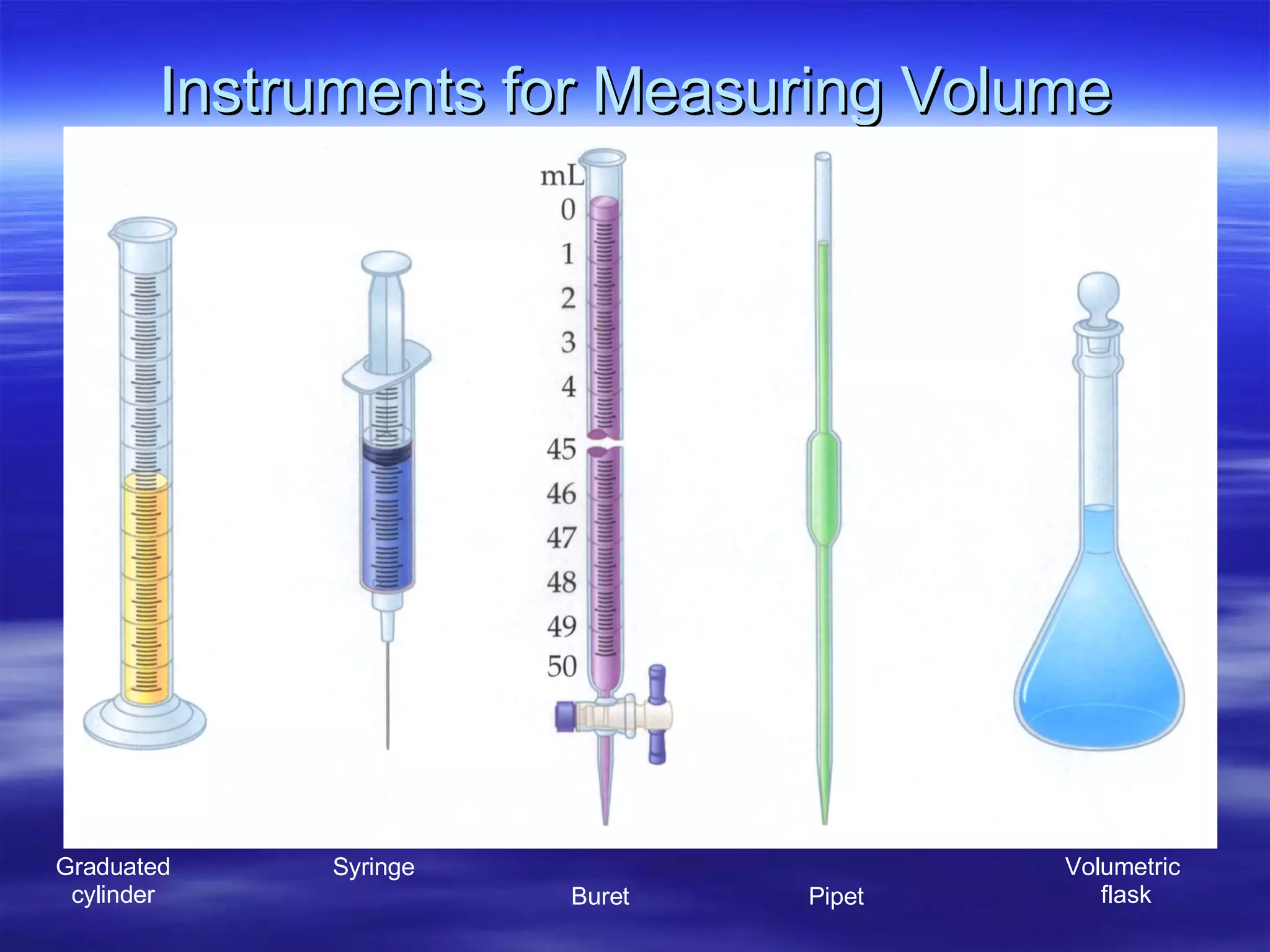
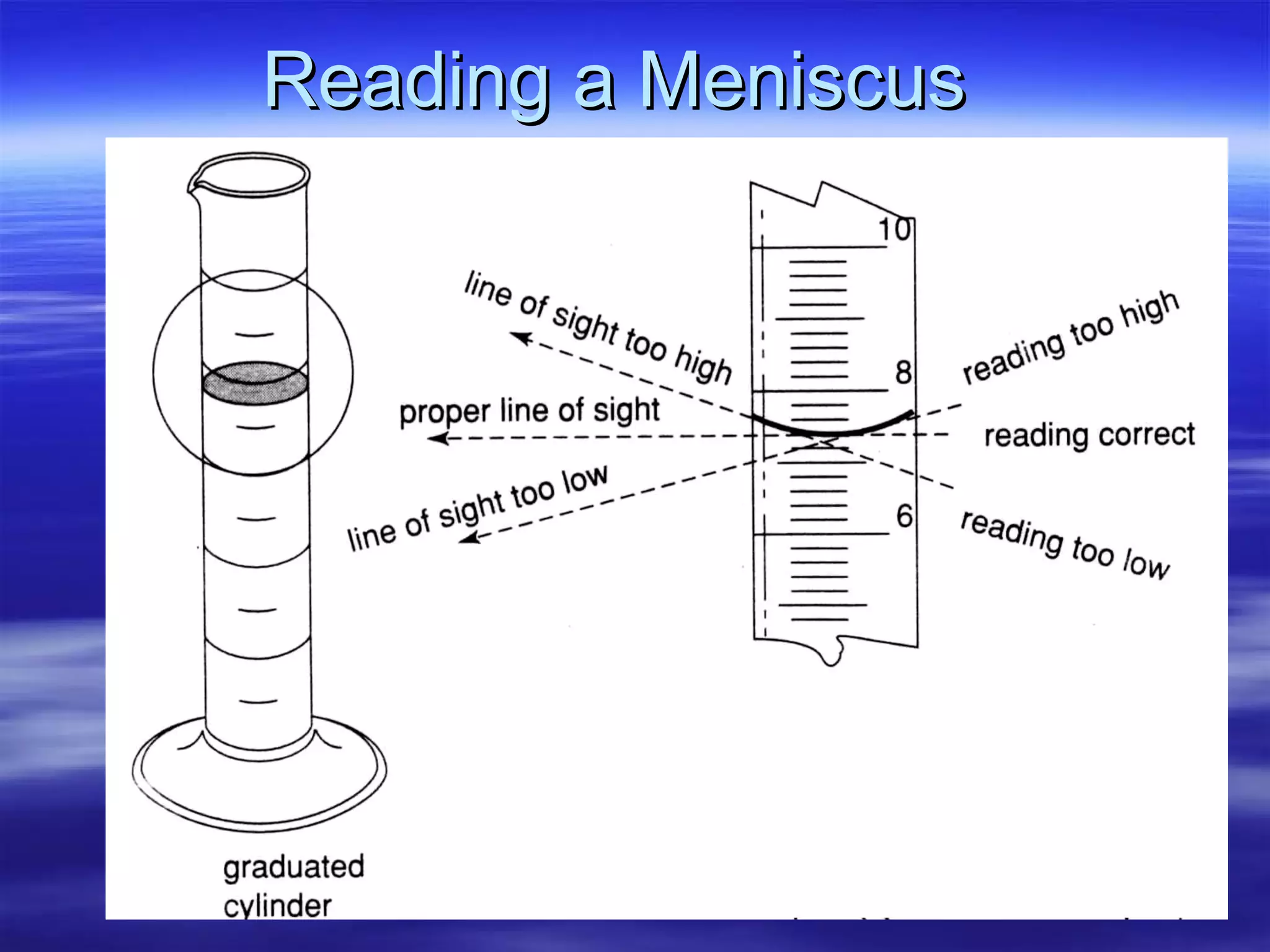
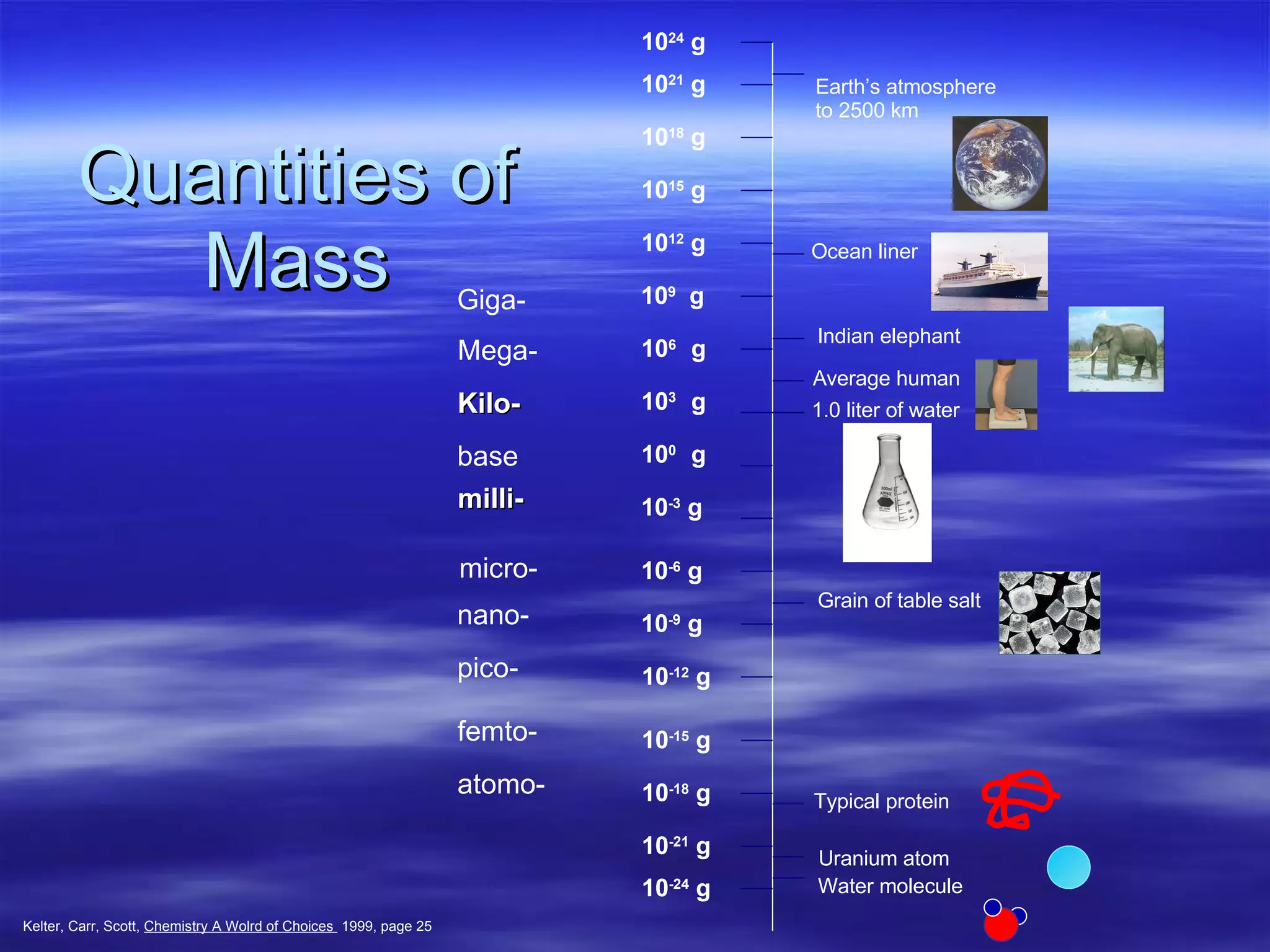
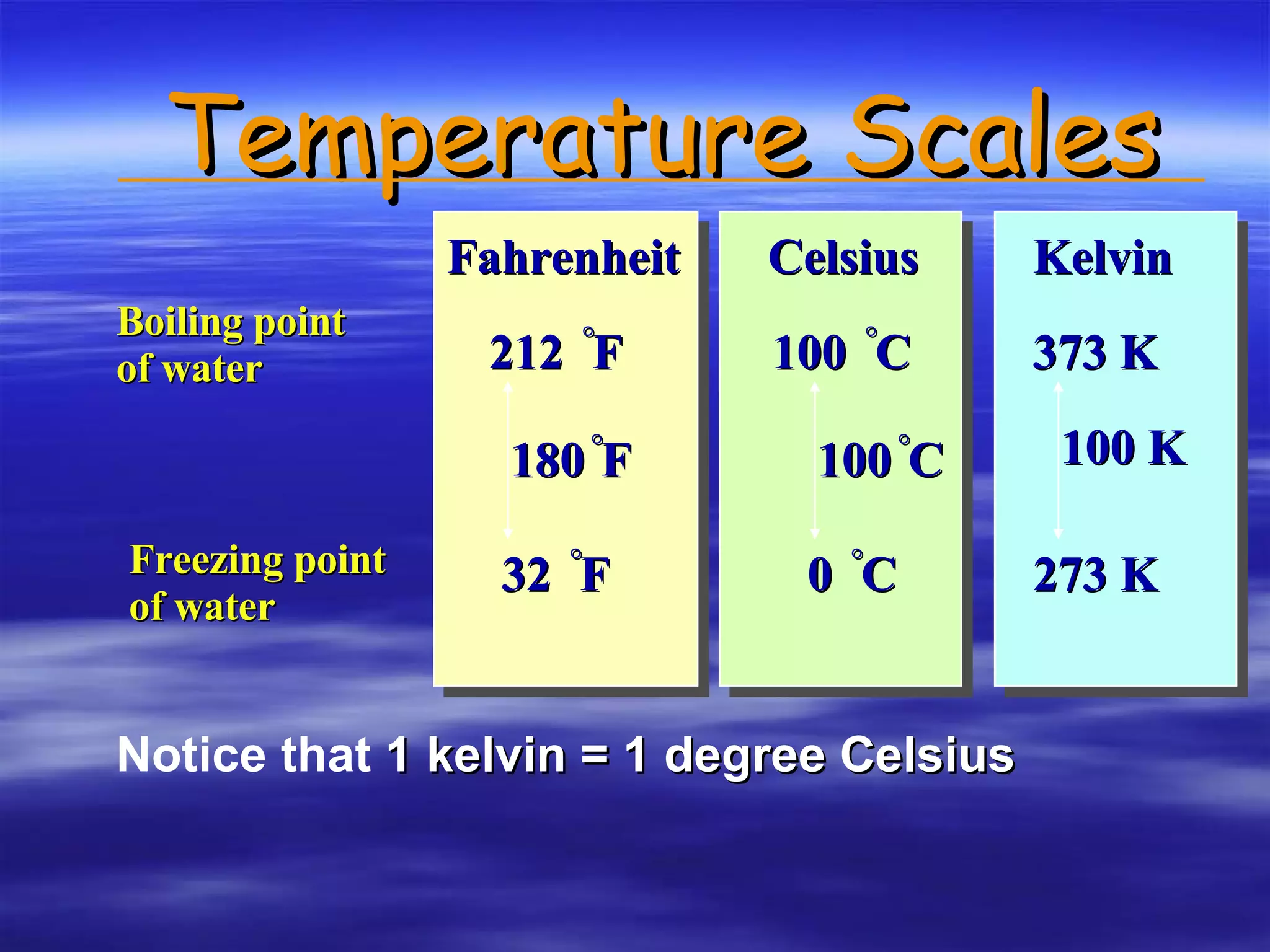
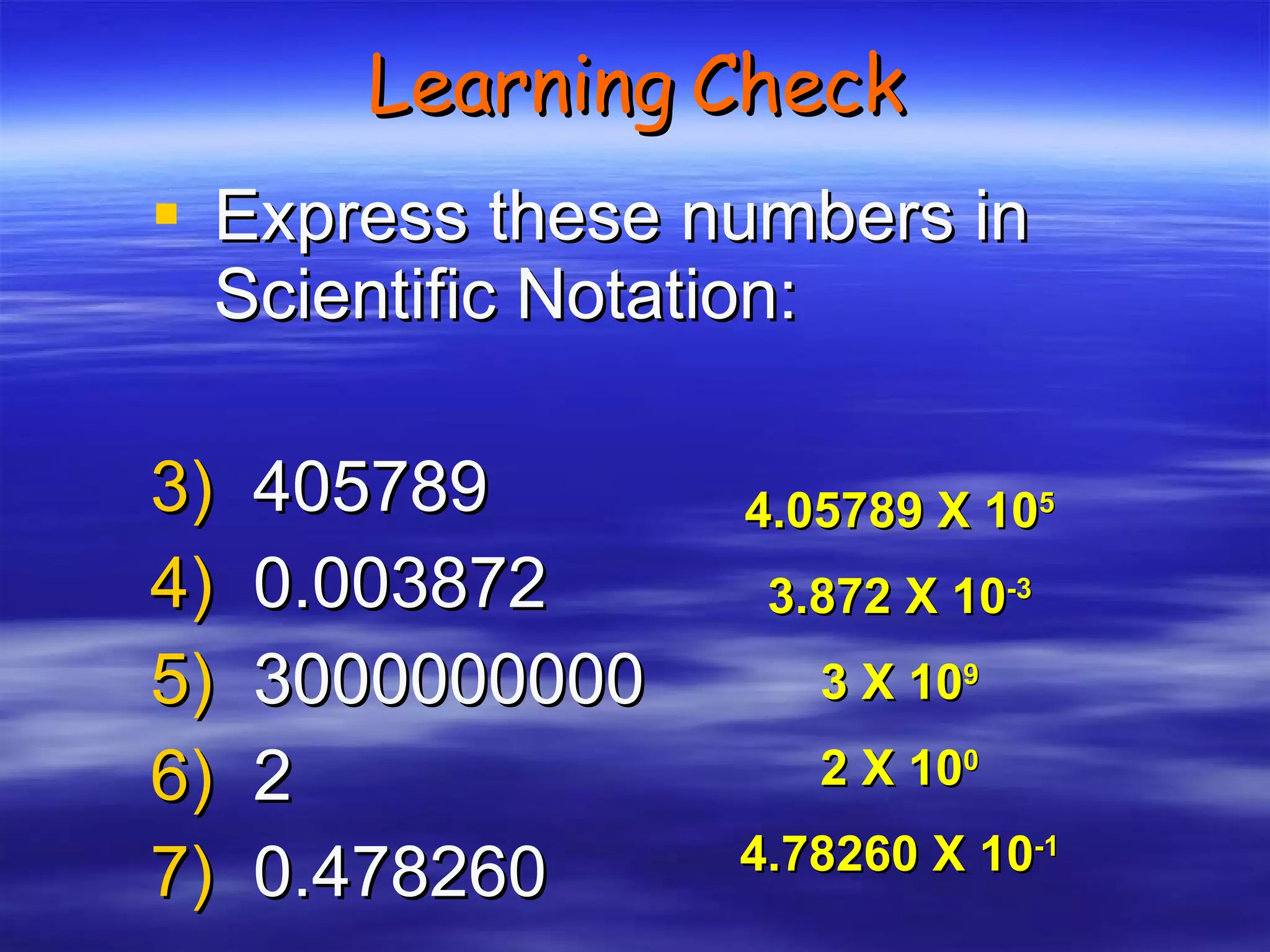
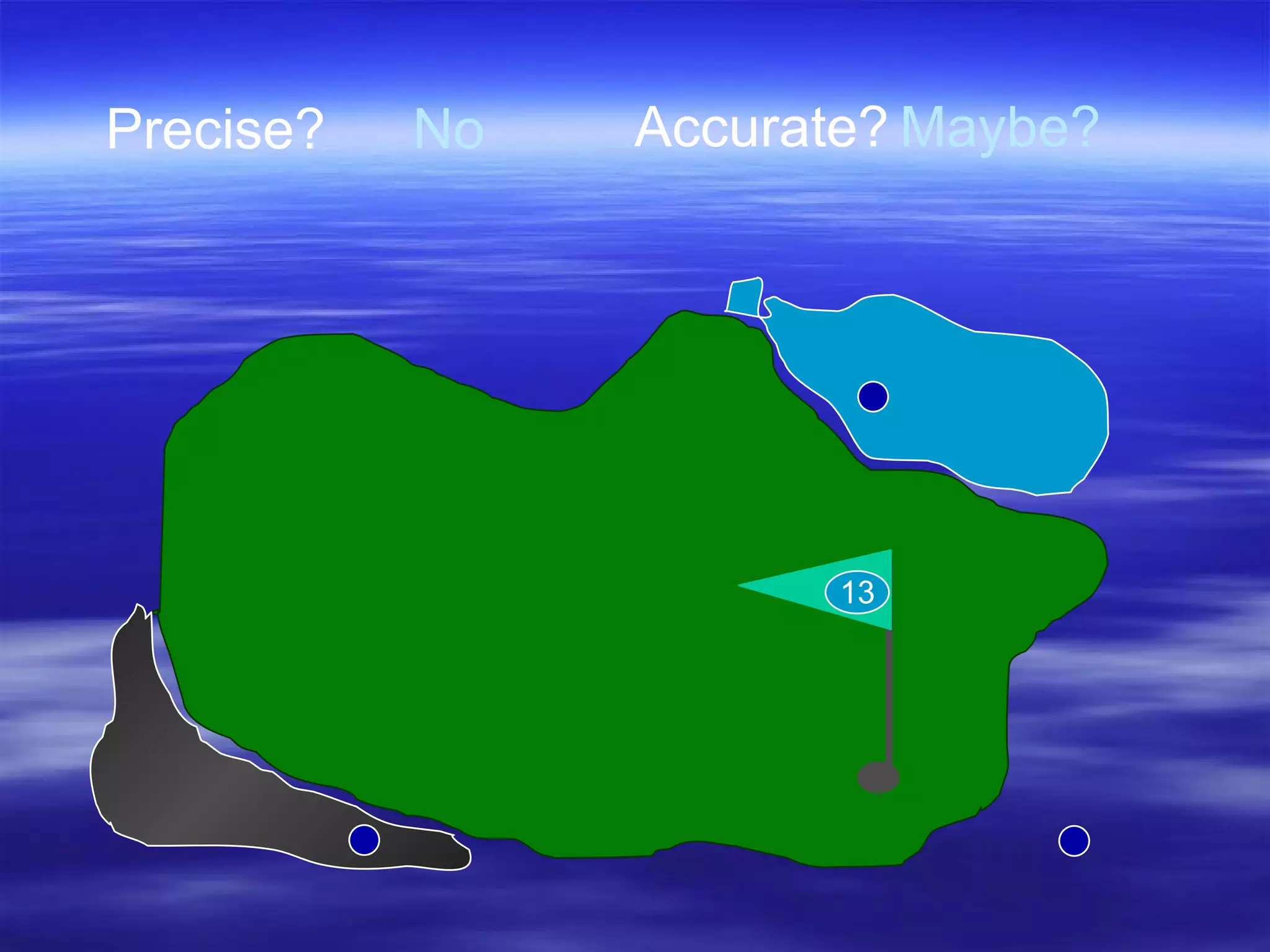
This document discusses measurement, density, and temperature scales. It defines qualitative and quantitative measurements. It explains scientific notation and how to convert between standard and scientific notation. It discusses accuracy versus precision. It describes metric units and prefixes for length, mass, volume, and temperature. It provides examples of calculating density and solving density problems using dimensional analysis. Finally, it introduces the Fahrenheit, Celsius, and Kelvin temperature scales.

1. Ch 3 Measurement and Density

11. Three targets with three arrows each to shoot. Can you hit the bull's-eye? Both accurate and precise Precise but not accurate Neither accurate nor precise How do they compare? Can you define accuracy and precision?

12. Let’s use a golf anaolgy

13. Accurate? No Precise? Yes 10

14. Accurate? Yes Precise? Yes 12

15. Precise? No Accurate? Maybe? 13

16. Accurate? Yes Precise? We cant say! 18

17. Accurate? Yes Precise? We cant say! 18

18. Accurate? Yes Precise? We cant say! 18

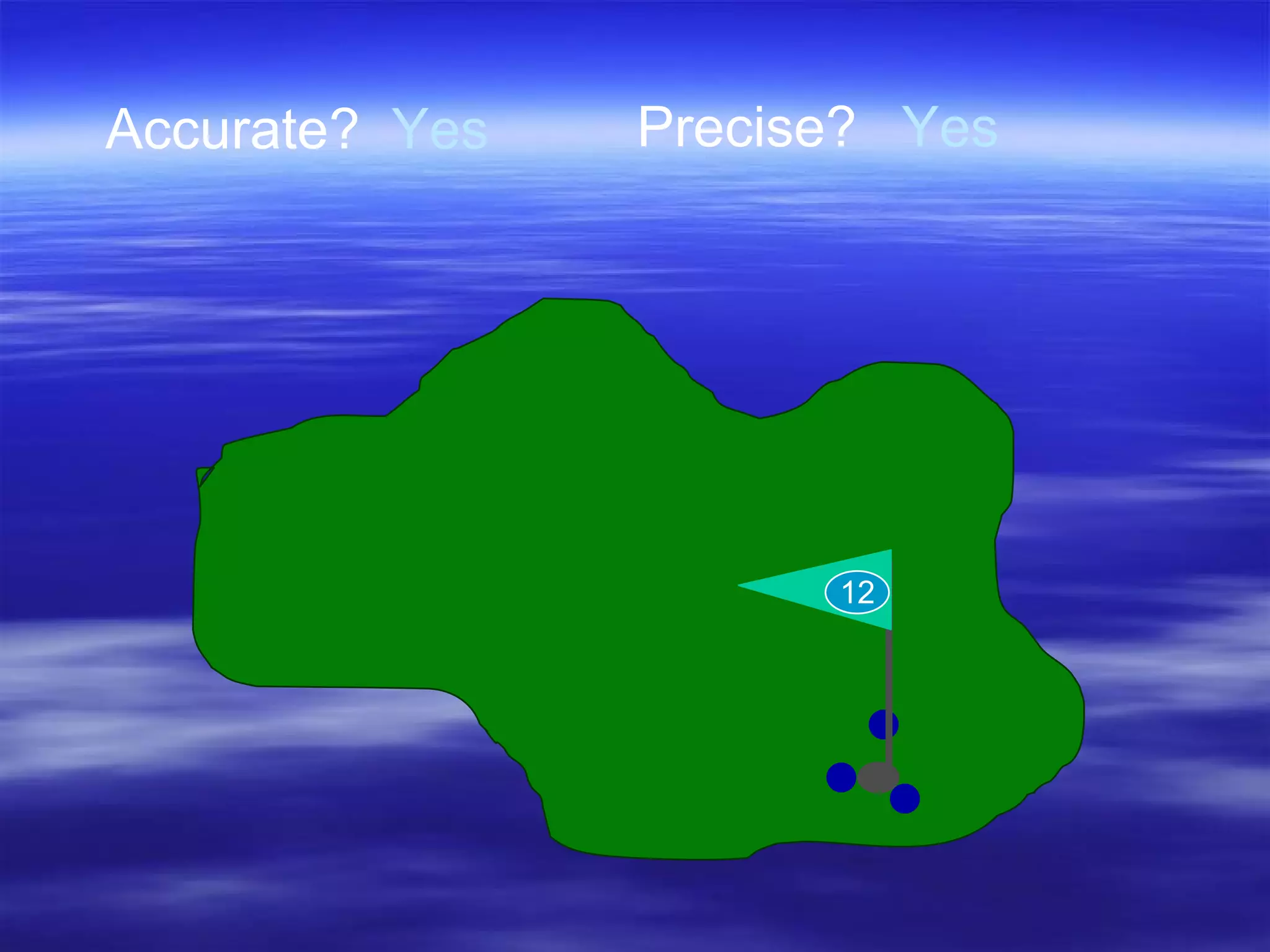
19. Accuracy Precision Resolution subsequent samples time offset [arbitrary units] not accurate, not precise accurate, not precise not accurate, precise accurate and precise accurate, low resolution -2 -3 -1 0 1 2 3

34. Some Tools for Measurement Which tool(s) would you use to measure: A. temperature B. volume C. time D. weight

40. Metric Prefixes

41. Metric Prefixes

48. Instruments for Measuring Volume Graduated cylinder Syringe Volumetric flask Buret Pipet

49. Units of Measuring Volume 1 L = 1000 mL 1 qt = 946 mL Timberlake, Chemistry 7 th Edition, page 3

50. Reading a Meniscus

51. Units for Measuring Mass 1 kg = 2.20 lb Timberlake, Chemistry 7 th Edition, page 3

52. Quantities of Mass Kelter, Carr, Scott, Chemistry A Wolrd of Choices 1999, page 25 Earth’s atmosphere to 2500 km Ocean liner Indian elephant Average human 1.0 liter of water Grain of table salt Typical protein Uranium atom Water molecule 10 24 g 10 21 g 10 18 g 10 15 g 10 12 g 10 9 g 10 6 g 10 3 g 10 0 g 10 -3 g 10 -6 g 10 -9 g 10 -12 g 10 -15 g 10 -18 g 10 -21 g 10 -24 g Giga- Mega- Kilo- base milli- micro- nano- pico- femto- atomo-

53. DENSITY - an important and useful physical property 13.6 g/cm 3 21.5 g/cm 3 2.7 g/cm 3 Mercury Aluminum Platinum

57. PROBLEM: Mercury (Hg) has a density of 13.6 g/cm 3 . What is the mass of 95 mL of Hg in grams? In pounds? Solve the problem using DIMENSIONAL ANALYSIS.

69. Temperature Scales Notice that 1 kelvin = 1 degree Celsius Boiling point of water Freezing point of water Celsius Kelvin Fahrenheit 100 ˚C 0 ˚C 100˚C 373 K 273 K 100 K 32 ˚F 212 ˚F 180˚F