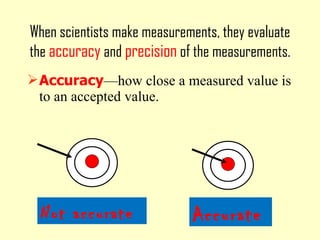
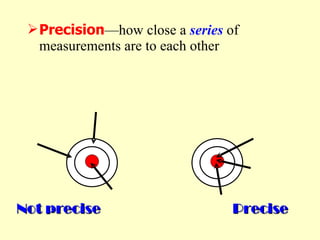
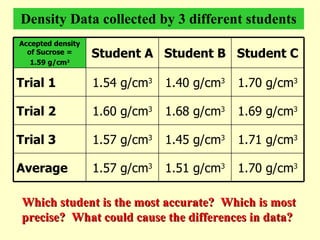
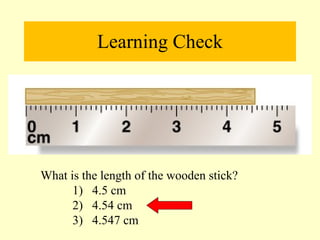
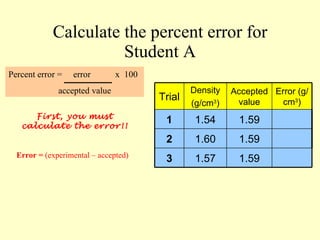
1. The document discusses units of measurement and the SI system. It describes the seven base SI units including meters, kilograms, seconds, and kelvins. 2. Derived units are discussed along with examples like density. Significant figures and the accuracy and precision of measurements are also covered. 3. Errors in measurements are defined as the difference between experimental and accepted values. Percent error can quantify the accuracy of a measurement.

1. Chapter 2: Data Analysis Section 1: Units of measurement

6. SI Base Units Quantity Base unit Time second (s) Length meter (m) Mass kilogram (kg) Temperature kelvin (K) Amount of substance mole (mol) Electric current ampere (A) Luminous intensity candela (cd)

14. Example: If a sample of aluminum has a mass of 13.5g and a volume of 5.0 cm 3 , what is its density? Density = mass volume D = 13.5 g 5.0 cm 3 D = 2.7 g/cm 3

15. Suppose a sample of aluminum is placed in a 25 ml graduated cylinder containing 10.5 ml of water. A piece of aluminum is placed in the cylinder and the level of the water rises to 13.5 ml. The density of aluminum is 2.7 g/cm 3 . What is the mass of the aluminum sample?

16. Practice Problems—pg. 29 # 1, 2, 3

20. Section 2.2 Scientific Notation and Dimensional Analysis

22. Change the following data into scientific notation. a. The diameter of the sun is 1 392 000 km. b. The density of the sun’s lower atmosphere is 0.000 000 028 g/cm 3 .

23. Practice probs. Pg. 32 #12, 13

25. Practice probs. Pg. 32 #14

28. Practice probs. Pg. 33 #15, 16

31. Practice: Convert 360 L to ml and to teaspoons:

33. Practice probs. Pg. 34 #17, 18

34. You can convert more than one unit at a time: What is a speed of 550 meters per second in kilometers per minute? HINTs: Convert one unit at a time! Units MUST be ACROSS from each other to cancel out!

35. Section 2.3 How reliable are measurements:

39. Density Data collected by 3 different students Which student is the most accurate? Which is most precise? What could cause the differences in data? Accepted density of Sucrose = 1.59 g/cm 3 Student A Student B Student C Trial 1 1.54 g/cm 3 1.40 g/cm 3 1.70 g/cm 3 Trial 2 1.60 g/cm 3 1.68 g/cm 3 1.69 g/cm 3 Trial 3 1.57 g/cm 3 1.45 g/cm 3 1.71 g/cm 3 Average 1.57 g/cm 3 1.51 g/cm 3 1.70 g/cm 3

41. Calculate the percent error for Student A Percent error = error x 100 accepted value First, you must calculate the error!! Error = (experimental – accepted) Trial Density (g/cm 3 ) Accepted value Error (g/cm 3 ) 1 1.54 1.59 2 1.60 1.59 3 1.57 1.59

42. Practice probs. Pg. 38 #29

49. Learning Check What is the length of the wooden stick? 1) 4.5 cm 2) 4.54 cm 3) 4.547 cm

52. Determine the number of significant figures in the following masses: a. 0.000 402 30 g b. 405 000 kg a. 0.000 402 30 g b. 405 000 kg 5 sig figs 3 sig figs

54. Practice probs. Pg. 39 # 31, 32

56. Practice probs. Pg. 41 #34

59. Practice probs. Pg. 41 # 35, 36 pg. 42 #37, 38