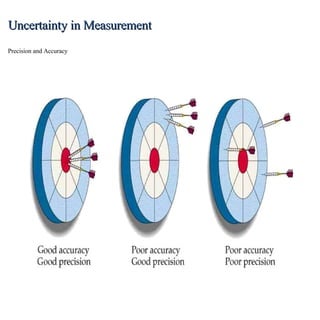
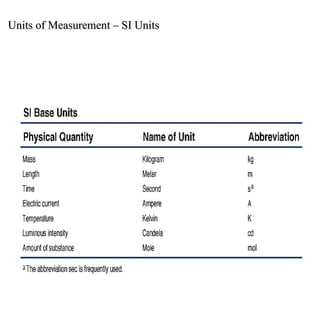
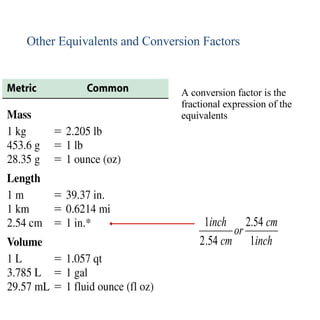
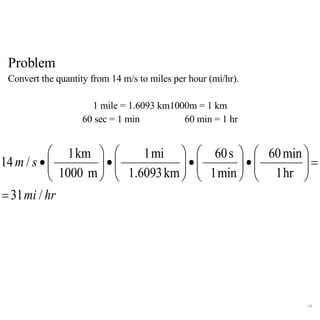
This lecture discusses scientific measurements and units. It covers the metric system and SI units, dimensional analysis, unit conversions, and significant figures. Key points include: 1. The metric system uses meters, grams, and seconds as fundamental units. There are seven base SI units including the meter for length and gram for mass. 2. Dimensional analysis uses conversion factors to change between units while maintaining the correct dimensions. It is useful for solving chemistry problems. 3. Significant figures indicate the precision of a measurement and how numbers should be rounded. Calculations are rounded according to whether they involve multiplication/division or addition/subtraction.

1. Md. Faysal Ahamed Khan Lecture 3 Welcome to the class of Chemistry I Course No. CHEM 211 Credit hours 3

2. Scientific Measurements and Units All measurements contain two essential pieces of information: a number (the quantitative piece) a unit (the qualitative piece) A measurement is useless without its units The number 60 is somewhat meaningless without units. Consider this for one’s wages: $ per week $ per hour

3. Measurement All measurements have three parts: 1. A value 26.976 2 g 2. Units 3. An Uncertainty Examples: 33.2 mL 72.36 mm 426 kg 31 people

4. Systems of Units - Standards of Measurement Imperial system English units imperial units U. S. Customary Units Metric system SI system Foot-pound-second systems Metre and gram Metre –kilogram-second system

5. The metric system is a decimalized system of measurement based on the metre and the gram . Both the Imperial units and US customary units derive from earlier English units . Imperial units were mostly used in the British Commonwealth and the former British Empire . US customary units are still the main system of measurement in the United States

6. Units of Measurement – SI Units There are two types of units: fundamental (or base) units; derived units. There are 7 base units in the SI system. Derived units are obtained from the 7 base SI units. Example:

7. Units of Measurement – SI Units

8. Common SI Prefixes

9. A Problem-Solving Method Chemistry problems usually require calculations, and yield quantitative (numerical) answers For example, 1 inch = 2.54 cm The unit-conversion method is useful for solving most chemistry problems – the focus here is on “unit equivalents”

10. Dimensional Analysis – Factor Label Method In dimensional analysis always ask three questions: What data are we given? What quantity do we need? What conversion factors are available to take us from what we are given to what we need?

11. Other Equivalents and Conversion Factors A conversion factor is the fractional expression of the equivalents

12. Dimensional Analysis Example: we want to convert the distance 8 in. to feet. (12in = 1 ft) Problem Convert the quantity from 2.3 x 10 -8 cm to nanometers (nm) First we will need to determine the conversion factors Centimeter (cm)  Meter (m) Meter (m)  Nanometer (nm) Or 1 cm = 0.01 m 1 x 10 -9 m = 1 nm

13. Dimensional Analysis Problem Convert the quantity from 2.3 x 10 -8 cm to nanometers (nm) 1 cm = 0.01 m 1 x 10 -9 m = 1 nm Now, we need to setup the equation where the cm cancels and nm is left. Now, fill-in the value that corresponds with the unit and solve the equation.

14. Problem Convert the quantity from 31,820 mi 2 to square meters (m 2 ) First we will need to determine the conversion factors Mile (mi)  kilometer (km) kilometer (km)  meter (m)

15. Problem Convert the quantity from 31,820 mi 2 to square meters (m 2 ) First we will need to determine the conversion factors Mile (mi)  kilometer (km), kilometer (km)  meter (km) Or 1 mile = 1.6093km, 1000m = 1 km Notice, that the units do not cancel, each conversion factor must be “squared”.

16. Problem Convert the quantity from 31,820 mi 2 to square meters (m 2 )

17. Problem Convert the quantity from 14 m/s to miles per hour (mi/hr). Determine the conversion factors Meter (m)  Kilometer (km) Kilometer(km)  Mile(mi) Seconds (s)  Minutes (min) Minutes(min)  Hours (hr) Or 1 mile = 1.6093 km 1000m = 1 km 60 sec = 1 min 60 min = 1 hr

18. Problem Convert the quantity from 14 m/s to miles per hour (mi/hr). 1 mile = 1.6093 km 1000m = 1 km 60 sec = 1 min 60 min = 1 hr

19. Dimensional Analysis How many mL are in 3.0 ft 3 ? 1 ft = 12 in 1 in = 2.54 cm 1 cm 3 = 1 mL (3.0 ft 3 )( 12 in )( 12 in )( 12 in) ( 2.54 cm )( 2.54 cm )( 2.54 cm )( 1 mL ) (1 ft) (1 ft) (1 ft) (1 in) (1 in) (1 in) (1 cm 3 ) = 8.5 x 10 4 mL How many ns are in 23.8 s? (23.8 s)( 10 9 ns ) (1 s) = 23.8 x 10 9 ns = 2.38 x 10 10 ns

20. Mass and Weight Mass: the measure of the quantity or amount of matter in an object. The mass of an object does not change as Its position changes. Weight: A measure of the gravitational attraction of the earth for an object. The weight of an object changes with its distance from the center of the earth. Sample Calculations Involving Masses How many mg are in 2.56 kg? (2.56 kg)(10 3 g)(10 6 mg) (1 kg) ( 1 g) = 2.56 x 10 9 mg

21. The units for volume are given by (units of length) 3 . i.e., SI unit for volume is 1 m 3 . A more common volume unit is the liter (L) 1 L = 1 dm 3 = 1000 cm 3 = 1000 mL. We usually use 1 mL = 1 cm 3 . Volume Sample Calculations Involving Volumes How many mL are in 3.456 L? (3.456 L)( 1000 mL ) L = 3456 mL How many ML are in 23.7 cm 3 ? (23.7 cm 3 )( 1 mL )( 1 L_ _ )( 10 6 ML) (1 cm 3 )(1000 mL)( 1L ) = 2.37 x 10 4 ML = 23 700 ML

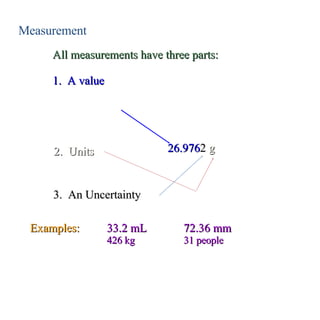
22. Density Density - The mass of a unit volume of a material. density = mass/volume What is the density of a cubic block of wood that is 2.4 cm on each side and has a mass of 9.57 g? volume = [2.4 cm x 2.4 cm x 2.4 cm] density = (9.57 g)/(13. 8 cm 3 ) = 0.69 g/cm 3 = 0.69 g/mL Note that 1 cm 3 = 1 mL

23. Temperature

24. Temperature Kelvin Scale Used in science. Same temperature increment as Celsius scale. Lowest temperature possible (absolute zero) is zero Kelvin. Absolute zero: 0 K = -273.15 o C. Celsius Scale Also used in science. Water freezes at 0 o C and boils at 100 o C. To convert: K = o C + 273.15. Fahrenheit Scale Not generally used in science. Water freezes at 32 o F and boils at 212 o F. Converting between Celsius and Fahrenheit

25. Sample Calculations Involving Temperatures Convert 73.6 o F to Celsius and Kelvin temperatures. o C = (5/9)(73.6 o F - 32) = (5/9)(41.6) o C = (5/9)( o F - 32) K = o C + 273.15 = 23.1 o C K = 23.1 o C + 273.15 = 296.3 K Memorize

26. All scientific measures are subject to error. These errors are reflected in the number of figures reported for the measurement. These errors are also reflected in the observation that two successive measures of the same quantity are different. Uncertainty in Measurement

27. Precision and Accuracy in Measurements Precision refers to how closely individual scientific measurements agree with one another. Accuracy refers to the closeness of the average of a set of scientific measurements to the “correct” or “most probable” value.

28. Measurements that are close to the “correct” value are accurate. Measurements which are close to each other are precise. Measurements can be accurate and precise precise but inaccurate neither accurate nor precise Uncertainty in Measurement Precision and Accuracy

29. Precision and Accuracy Uncertainty in Measurement

30. Uncertainty in Measurement The number of digits reported in a measurement reflect the accuracy of the measurement and the precision of the measuring device. All the figures known with certainty plus one extra figure are called significant figures. The more significant digits obtained, the better the precision of a measurement The concept of significant figures applies only to measurements In any calculation, the results are reported to the fewest significant figures (for multiplication and division) or fewest decimal places (addition and subtraction). Significant Figures

31. Non-zero numbers are always significant. Zeros between two other significant digits ARE significant e.g., 1 00 23 A zero preceding a decimal point is not significant e.g., 0.1 00 23 Zeros between the decimal point and the first nonzero digit are not significant e.g., 0.001 00 23 Rules for Zeros in Significant Figures Uncertainty in Measurement

32. Zeros at the end of a number are significant if they are to the right of the decimal point e.g., 0.1 00 23 00 1 0 23. 00 Zeros to the right of all nonzero digits in an integer (for example 5 00 ) are uncertain. If they indicate only the magnitude of measurement, they are not significant. However, if they also show something about the precision of the measurement, they are significant. Example – so for the number 10,300 has 3 significant figures and the rests are uncertain Uncertainty in Measurement

33. If the leftmost digit to be dropped is less than 5, the preceding number is left unchanged. “Round down.” Example: 7.5 5 4 3 cm = 7.55 cm -7.5 5 4 3 cm = -7.55 cm If the leftmost digit to be dropped is 5 or greater, the preceding number is increased by 1. “Round up.” Example: 7.5 5 6 1 cm = 7.56 cm -7.5 5 6 1 cm = -7.56 cm Rounding rules Uncertainty in Measurement

34. Multiplication / Division The result must have the same number of significant figures as the least accurately determined data Example: 12.512 (5 sig. fig.) x 5.1 (2 sig. fig.) 12.512 x 5.1 = 64 Answer has only 2 significant figures Q1: 7.07 g/2.02 cm 3 = 3.50 g/ cm 3 Q2: 8.2 cm x 4.001 cm = 32.8082 cm 2 = 33 cm 2 Significant Figures Uncertainty in Measurement

35. Addition and Subtraction: the reported results should have the same number of decimal places as the number with the fewest decimal places NOTE - Be cautious of round-off errors in multi-step problems. Wait until calculating the final answer before rounding. Uncertainty in Measurement

36. Example: 15.152 (5 sig. fig., 3 digits to the right), 1.76 (3 sig. fig., 2 digits to the right), 7.1 (2 sig. fig., 1 digit to the right). 15.152 + 1.76 + 7.1 = 24.0 24.0 (3 sig. fig., but only 1 digit to the right of the decimal point) Significant Figures Uncertainty in Measurement