1. The document discusses various topics related to stress analysis including moment of inertias, stresses from different load cases, principal stresses, stress states, stresses in cylinders, and deflection analysis using Castigliano's theorem. 2. Design considerations for static strength are covered for both ductile and brittle materials using theories such as maximum normal stress and distortion energy. 3. Fatigue strength design includes determining the endurance limit based on material properties and adjusting it using factors for surface finish, size, and loading conditions.

1. 1. Stress Analysis
Moment of Inertias
1. Atalet moment of inertia; 2. Polar moment of inertia;
2
x I   y dA
2
y I   x dA
2 2
( ) z J   x  y dA
Shape Ix Iy J
Rectangle bh3/12 hb3/12  2 2
12
bh
b h
Triangle bh3/36 hb3/36 2 2
18
h b
bh
  
 
 
 
Circle πd4/64 πd4/64 πd4/32
Stresses
Normal Stresses Shear Stresses
Axial
Tensile
F
A
 
Torsional
Tr
J
 

3
Compression   16T / d for solid circular beam
F
A
 
Bending
b
Mc
I
 

3
32
b
M
d


 for solid circular beam
Transverse
(Flexural)
VQ
Ib
  , Q A y


 max   4V / 3A for solid circular beam
 max   2V / A for hollow circular section
 max   3V / 2A for rectangular beam
Principle stresses
2
2
1,2
2 2
x y x y
xy
   
 
  
  
 
 
 
2
tan 2
xy
x y


 


Max. and min shear stresses
2
2
1,2
2
x y
xy
 
 
 
  
 
 
 
Von-Mises stresses
2 2
1 1 2 2  '      or 2 2
' 3 x xy      (for biaxial)
Stress States
Triaxial stress state
1 2 3
1
E E
  
 

 
2 1 3
2
E E
  
 

 
3 1 2
2
E E
  
 

 
Stress in Cylinders
Thick-Walled (t/r>1/20) Wessels (internally and externally pressurized cyclinders):
2 2 2 2 2
2 2
( ) / i o o i
t
p a p b a b p p r
b a

  


2 2 2 2 2
2 2
( ) / i o o i
r
p a p b a b p p r
b a

  


2
2 2
i
l
p a
b a
 


2.  If the external pressure is zero (po=0);
2 2
2 2 2
1 i
t
a p b
b a r
  

 
 
 
2 2
2 2 2
1 i
r
a p b
b a r
  

 
 
 
r=a  r   pi
2 2
t i 2 2
b a
p
b a




r=b 0 r  
2
2 2
2
t i
a
p
b a
 

 If the internal pressure is zero (pi=0);
2 2
2 2 2
1 t o
b a
p
b a r
   

 
 
 
2 2
2 2 2
1 r o
b a
p
b a r
   

 
 
 
r=a  0 r  
2
2 2
2
t o
b
p
b a
  

r=b r o    p
2 2
t o 2 2
b a
p
b a


 

a=inside radius of the cylinder b=outside radius of the cylinder pi=internal pressure po=external pressure
Thin-Walled Wessels(t/r<1/20):
2
i
t
pd
t
 
4
i
l
pd
t
 
Curved Members In Flexure:

A
r
dA




( )
My
Ae r y
 

 o
o
o
Mc
Aer
  , i
i
i
Mc
Aer
 
Press and Shrink Fit:

2 2
it 2 2
b a
p
b a


 


2 2
ot 2 2
c b
p
c b


 


2 2
o 2 2 o
o
bp c b
E c b
 

 

 
 
 

2 2
i 2 2 i
i
bp b a
E b a
 

  

 
 
 

2 2 2 2
o i 2 2 o 2 2 i
o i
bp c b bp b a
E c b E b a
      
 
   
 
   
   
   

  
 
2 2 2 2
2 2 2
; interface pressure
2
o i
E c b b a
if E E E = p =
b b c a
  
 

 
 
 

3. 2. Deflection Analysis
F
k
y
 , k=spring constant
T GJ
k
 l
  ,k=Torsional spring rate for tension or compression loading
AE
k
l

Castigliano’s Theorem:
Strain Energy
Axial Load
2
2
F L
U
AE
 Direct Shear Force
2
2
F L
U
AG

Torsional Load
2
2
T L
U
GJ
 Bending Moment
2
2
M
U dx
EI
 
Flexural Shear
2
2
CF
U dx
GA
  , C is constant
Buckling Consideration:
Slenderness ratio=
l
k
 
 
 
,
I
k
A

1/2
1
l 2 EC
k Sy


   
         

 
 
2
2
1
Critical Unit Load = Euler Column
/
cr l l P C E
k k A l k

  
   
   
   
;
2
2
P
cr
C EI
l


  
2 2
1
1
Critital Unit Load Johnson's Column
2
cr y
y =
l l P S l
= S
k k A  CE k
  
        
        
        
1. Both ends are rounded-simply supported C=1
2. Both ends are fixed C=4
3. One end fixed, one end rounded and guided C=2
4. One end fixed, one end free C=1/4
U Total energy
F Force on the deflection point
 Angular deflection
U
y
F



Tl
GJ
 

4. 3.Design For Static Strength
Ductile Materials
1. Max. Normal Stress Theory (MNST):
 If, 1 2 3   

1
y S
n


3. Distortion Energy Theory
 If, 1 2 3   

2 2 2
1 2 2 3 3 1 ( ) ( ) ( )
'
2
     

    

 For baxial stress state;
2 2
' 3 x xy     
 1
y S
n


2. Max. Shear Stress Theory (MSST):
 Yield strength in shear (Ssy)=Sy/2

  1 3
max
2
 


 , for biaxial stress state;
max
1 2 2
4
2
x xy     

max
sy S
n


Brittle Materials
1. Max. Normal Stress Theory (MNST): 3. The Modified Mohr Theory (MMT)
 If, 1 2 3    
1
ut S
n

 or
3
uc S
n


 If, 1 2 3   
 3
1
3
1
uc
uc ut
ut
S
S
S S
S





 3
3
S
n


2. The Column Mohr Theory (CMT) or Internal
Friction Theory (IFT):
 3
1
3
1
uc
uc
ut
S
S
S
S




 3
3
S
n



5. 5. Design for Fatigue Strength
Endurance limit for test specimen (Se’);
 For ductile materials:
Se’=0.5 Sut if Sut<1400 MPa
Se’=700 MPa if Sut  1400 MPa
 For irons:
Se’=0.4 Sut if Sut<400 MPa
Se’=160 MPa if Sut  400 MPa
 For Aliminiums:
Se’=0.4 Sut if Sut<330 MPa
Se’=130 MPa if Sut  330 MPa
 For copper alloys:
Se’  0.4 Sut if Sut<280 MPa
Se’  100 MPa if Sut  280 MPa
Se = ka kb kc kd ke Se’
Sf=10c Nb
u
e
1 0.8S
b log
3 S
 
   
 
 2
u
e
0.8S
c log
S
 
  
 
 ka= surface factor, ka=aSut
b
Surface Finish Factor a Factor b
Ground 1.58 -0.065
Machined or Cold Drawn 4.51 -0.265
Hot Rolled 57.7 -0.718
As Forged 272 -0.995
 kb= size factor;
kb=1 if d  8 mm and kb= 1.189d-0.097 if 8 mm<d  250 mm for bending & torsional loading.
For non-rotating element, 0.097
b eq k 1.189d   deq=0.37d
For pure axial loading, kb=1 and Se’=0.45Sut
For combined loading,  =1.11 if Sut  1520 MPa and  =1 if Sut  1520 MPa for ductile materials.
 kc=reliability factor
 kd=temperature effects, kd=1 if T 3500 and kd=0.5 if 3500<T 5000
 ke=stress concentration factor, ke=1/Kf Kf=1+q(Kt-1)
Kt=geometric stress concentration factor, q=notch sensitivity.
Modified Goodman Soderberg
Infinite Life Finite Life Infinite Life Finite Life
a m
e u
1
n =
σ σ
+
S S
a m
f u
1
n =
σ σ
+
S S
a m
e y
1
n =
σ σ
+
S S
a m
f y
1
n =
σ σ
+
S S
 Fa=(Fmax-Fmin)/2  Fm=(Fmax+Fmin)/2

6. 6. Tolerances and Fits
TF=Cmax-Cmin dL=DU-c Cmax=DU-dL Cmin=DL-dU
TF=Imax+Cmax dU=dL+TS Imax=dU-DL Imin=dL-Du
TF=Imax-Imin dU=DL+Imax
TS=dU-dL TH=DU-DL TF=TH+TS
7. Design of Power Screws
m m
R
m
Fd L d
T
2 d L
    
  
   
m m
L
m
Fd d L
T
2 d L
    
  
   
Or considering   tan ;
  m
R
Fd
T tan
2
      m
R
Fd
T tan
2
   
If the friction between the stationary member and the collar of the screw is taken into consideration;
  m c c
R
Fd d F
T tan
2 2

       m c c
R
Fd d F
T tan
2 2

    
o
R R
T FL
T 2 T
  

when collar friction is negligible, we obtain  as,
 
tan
tan

 
  
If   tan or
m
L
d
then screw is self locking.
 Bearing Stresses
  b 2 2
r
4pF
h d d
 
 
b
m
Fp
d th
 

p
t
2

 Shear Stresses
For Screw Thread For Nut Thread
s
r
2F
d h
 

n
2F
dh
 

 Bending Stresses
The maximum bending stress,
m
6F
d Np
 

N=h/p

7.  Tensile or Compressive stresses
x
t
F
A
 
2
t
t
d
A
4

 r m
t
d d
d
2


 Combined Stresses
R
xy 3
t
16T
d
 

Based on distortion energy theory;
R
xy 3
t
16T
d
 

2 2
'  x 3xy y S
n
'


Based on maximum shear stres theory;
2 2
max x xy
1
4
2
     sy
max
S
n 

8. Design of Bolted Joints
Fe=Feb+Fep Feb=CFe Fep=(1-C)Fe b
b m
k
C =
k  k
Fb=Fi+CFe Fm=Fi-(1-C)Fe
b b
b
A E
k
L

m 1 2 n
1 1 1 1
..........
k k k k
   
i
b
b
F
k
  i
m
m
F
k
 
 Shigley and Mishke approach;
For cone angle of 0   30 ,
i
i
i
i
1.813E d
k
1.15L 0.5d
ln 5
1.15L 2.5d

  
 
  
m 1 2 n
1 1 1 1
..........
k k k k
   
If L1=L2=L/2 and materials are same, m
1.813Ed
k
2.885L 2.5d
2ln
0.577L 2.5d

  
 
  

8. For cone angle of 0   45 ,
 
 
i
i
i
i
E d
k
5 2L 0.5d
ln
2L 2.5d


  
    
If L1=L2=L/2 and materials are same, m
Ed
k
L 0.5d
2ln 5
L 2.5d


  
 
  
 Wileman approach;
(Bid/L)
m i k  EdA e
Where Ai and Bi are constants related to the material. For Steel Ai=0.78715 and Bi=0.62873, for
Aliminium Ai=0.79670 and Bi=0.63816, for Gray cast iron Ai=0.77871 and Bi=0.61616.
 Filiz approach;
1
d
B
5 L
m eq
2
1
k E d e
2 1 B
   
   
   


1 2
eq
1 2
E E
E
E E


2
1
0.1d
B
L
 
 
 
8
1
1
2
L
B 1
L
 
   
 
Static loading;
b y t F  S A or b p t F  S A   p y S  0.85S mF  0
  e i p t e 1C nF  F  S A CnF n=load factor of safety
Critical load= i
ce
F
F
1 C


Dynamic Loading:
e
a
t
CnF
2A
  i
m a
t
F
A
    s
a m
e u
1
n
S S

 

t u e u
i
s e
A S CnF S
F 1
n 2 S
 
    
 
Fi=the maximum value of preload for there is no fatigue failure.
Limitations:
 p i p 0.6F  F  0.9F where p t p F  A S
 e ut
imax t ut
e
cF n S
F A S 1
2N S
 
    
 
 e e
i t p
F cF
(1 c) F A S
N N
    b 3.5d  c 10d b
180
c
N



9. 9. Design of Riveted Joints
 Shearing of Rivets:
F
A
  , F=Force on each rivet
2 d
A
4


 Secondary Shear Force
i
i N
2
i
1
Mr
F ''
r



 Bearing (compression) Failure:
F
A
   , A=td, t=thickness of the plate
 Plate Tension Failure:
F
A
  , A  w Nd t
w=width of plate
N=number of rivets on the
selected cross section

 Primary Shear Force
N
i
1
F
F'
A



10. Design of Welded Joints
 Primary Shear Stress
F
'
A
 
 u J  0.707hJ 
 Secondary Shear Stress
Mr
''
J
 
 u I  0.707hI 
 Bending Stress
Mc
I
 


10. Table 9-3 Minimum weld-metal properties
AWS electrode
Number
n
Tensile Strength
MPa
Yield Strength
MPa
Percent
Elongation E60xx 420 340 17-25 E70xx 480 390 22 E80xx 530 460 19 E90xx 620 530 14-17 E100xx 690 600 13-16 E120xx 830 740 14
Table 9-5 Fatigue-strength reduction factors
Type of Weld
Kf Reinforced butt weld 1.2 Toe of transverse fillet weld 1.5 End of parallel fillet weld 2.7 T-butt joint with sharp corners 2.0

11. Table 9-1 Torsional Properties of Fillet Welds*
Weld
Throat Area
Location of G
Unit Polar Moment of Inertia
*G is centroid of weld group; h is weld size; plane of torque couple is in the plane of the paper; all welds are of the same size.

12. Table 9-2 Bending Properties of Fillet Welds*
Weld
Throat Area
Location of G
Unit Moment of Inertia
*Iu, unit moment of inertia, is taken about a horizontal axis through G, the centroid of the weld group; h is weld size; the plane of the bending couple is normal to the paper; all welds are of the same size

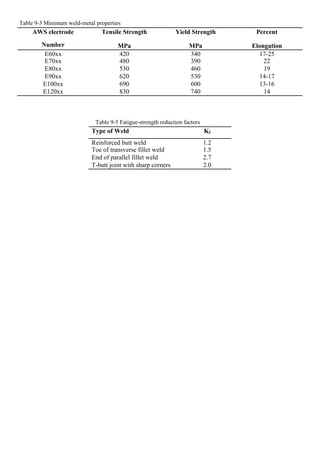
13. Table A3-8 Stress concentration factors for round shaft with
shoulder fillet in tension
d
r
D
.
o= F/A, where A= d2/4
D/d =1,02 D/d =1,05 D/d =1,1 D/d=1,5
r/d Kt Kt Kt Kt
0,025 1,800 - - -
0,028 1,728 - 2,200 -
0,031 1,678 2,000 2,125 -
0,037 1,610 1,868 2,020 -
0,044 1,550 1,778 1,938 2,522
0,050 1,508 1,714 1,866 2,400
0,062 1,452 1,626 1,766 2,235
0,075 1,408 1,550 1,684 2,086
0,088 1,370 1,502 1,624 1,970
0,100 1,336 1,457 1,568 1,893
0,125 1,286 1,400 1,496 1,760
0,150 1,254 1,364 1,452 1,662
0,175 1,230 1,340 1,400 1,600
0,200 1,220 1,314 1,372 1,546
0,250 1,216 1,292 1,342 1,508
0,275 1,200 1,270 1,325 1,480
0,300 1,200 1,250 1,296 1,452
* Adopted from Ref. [12]

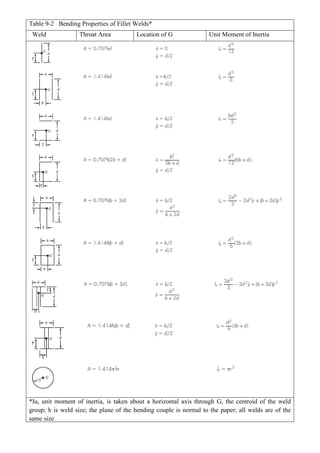
14. Table A3-9 Stress concentration factors for round shaft with shoulder fillet
in torsion
d
r
D
T T
.
o= Tc/J, where c=d/2 and J=d4/32
D/d =1,09 D/d =1,20 D/d =1,33 D/d =2,0
r/d Kt Kt Kt Kt
0,009 - - - -
0,012 1,800 2,300 - 2,600
0,030 1,566 2,040 2,144 2,288
0,025 1,472 1,894 2,020 2,122
0,033 1,384 1,761 1,878 1,966
0,042 1,322 1,644 1,755 1,828
0,050 1,283 1,576 1,677 1,750
0,062 1,244 1,500 1,600 1,644
0,075 1,206 1,434 1,516 1,572
0,087 1,184 1,378 1,458 1,510
0,100 1,166 1,342 1,412 1,466
0,125 1,144 1,275 1,344 1,400
0,150 1,122 1,220 1,294 1,344
0,200 1,110 1,160 1,220 1,266
0,250 1,100 1,130 1,178 1,222
0,300 1,100 1,120 1,160 1,200
* Adopted from Ref. [12]

15. Table A3-10 Stress Concentration factors for round shaft with shoulder
fillet in bending
d
r
M D M
.
o= Mc/I, where c=d/2 and I=d4/64
D/d =1,02 D/d =1,05 D/d =1,1 D/d =1,5 D/d =3
r/d Kt Kt Kt Kt Kt
0,012 2,290 2,553 2,700 - -
0,017 2,120 2,378 2,500 3,000 -
0,021 2,000 2,240 2,366 2,774 3,000
0,025 1,926 2,134 2,260 2,600 2,862
0,036 1,760 1,936 2,046 2,310 2,600
0,050 1,644 1,782 1,865 2,060 2,310
0,062 1,574 1,700 1,750 1,925 2,140
0,075 1,518 1,628 1,688 1,800 1,986
0,087 1,472 1,563 1,630 1,728 1,880
0,100 1,440 1,534 1,580 1,660 1,804
0,125 1,380 1,468 1,500 1,584 1,684
0,150 1,330 1,412 1,450 1,510 1,584
0,175 1,297 1,358 1,400 1,450 1,510
0,200 1,264 1,336 1,360 1,400 1,457
0,225 1,242 1,308 - - 1,410
0,250 1,225 1,286 - - 1,374
0,275 1,210 1,264 - - 1,340
0,300 1,200 1,242 - - 1,320
* Adopted from Ref. [12]