Download as PDF, PPTX
Uploaded byDeepak Agarwal
Lecture 2 principal stress and strain
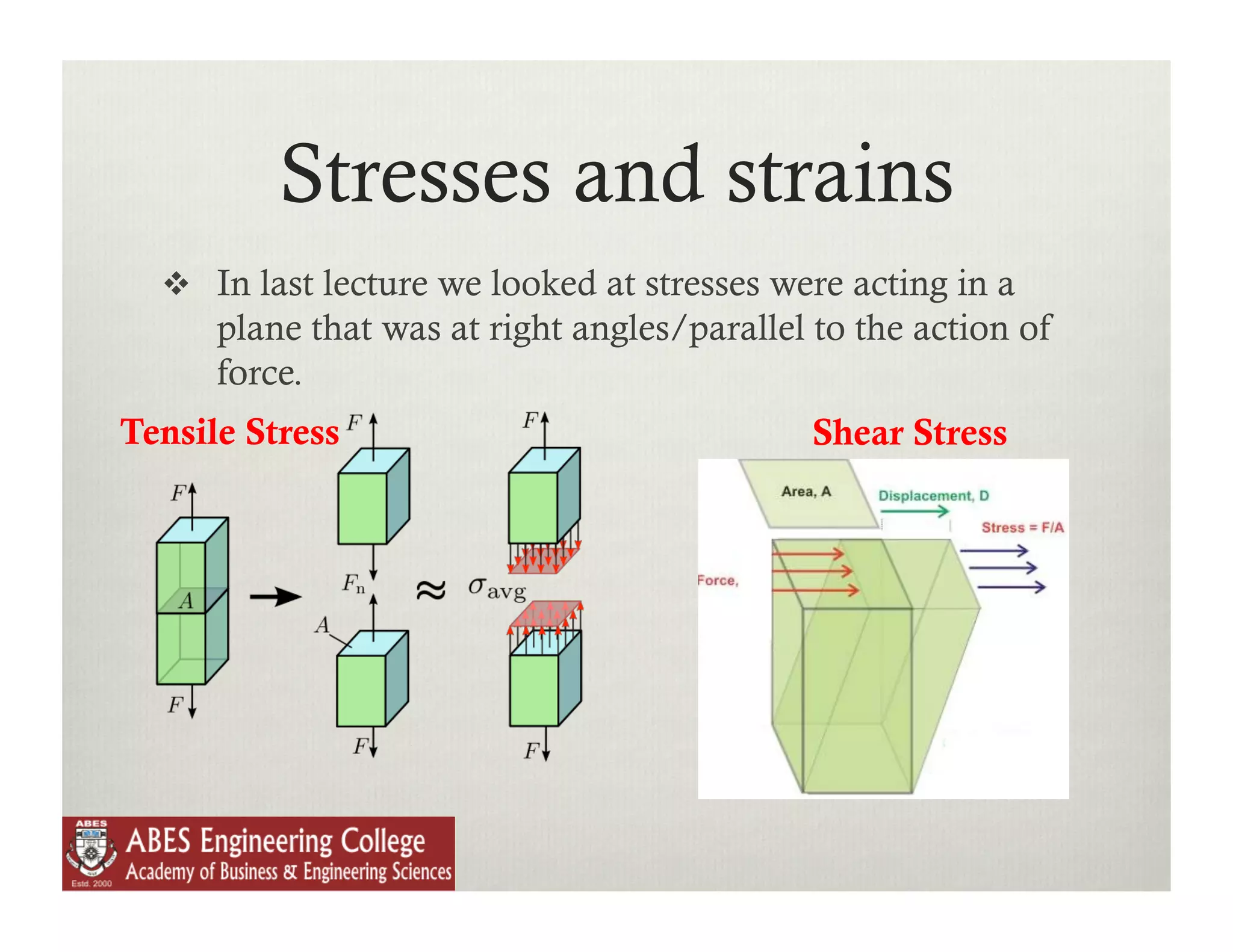
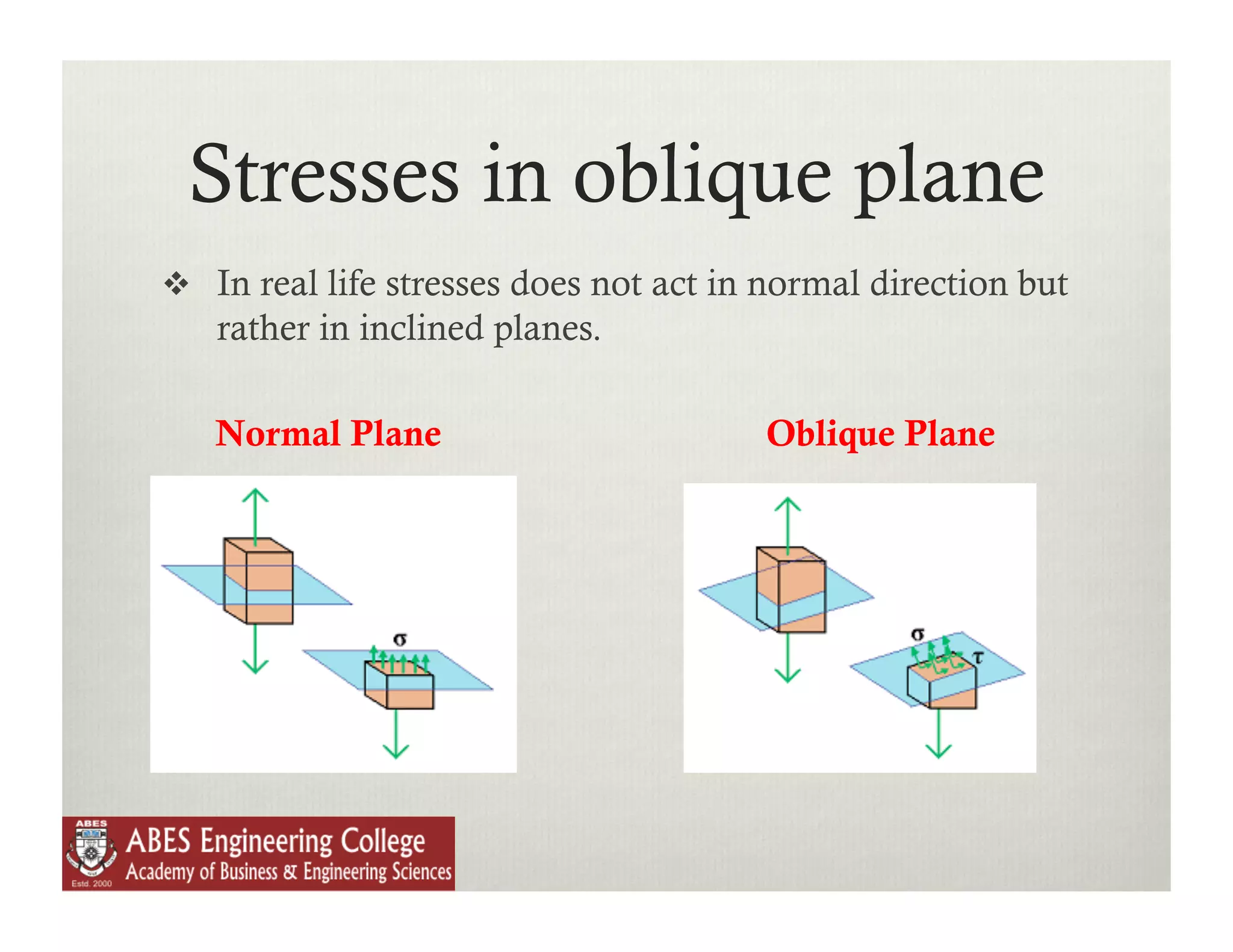
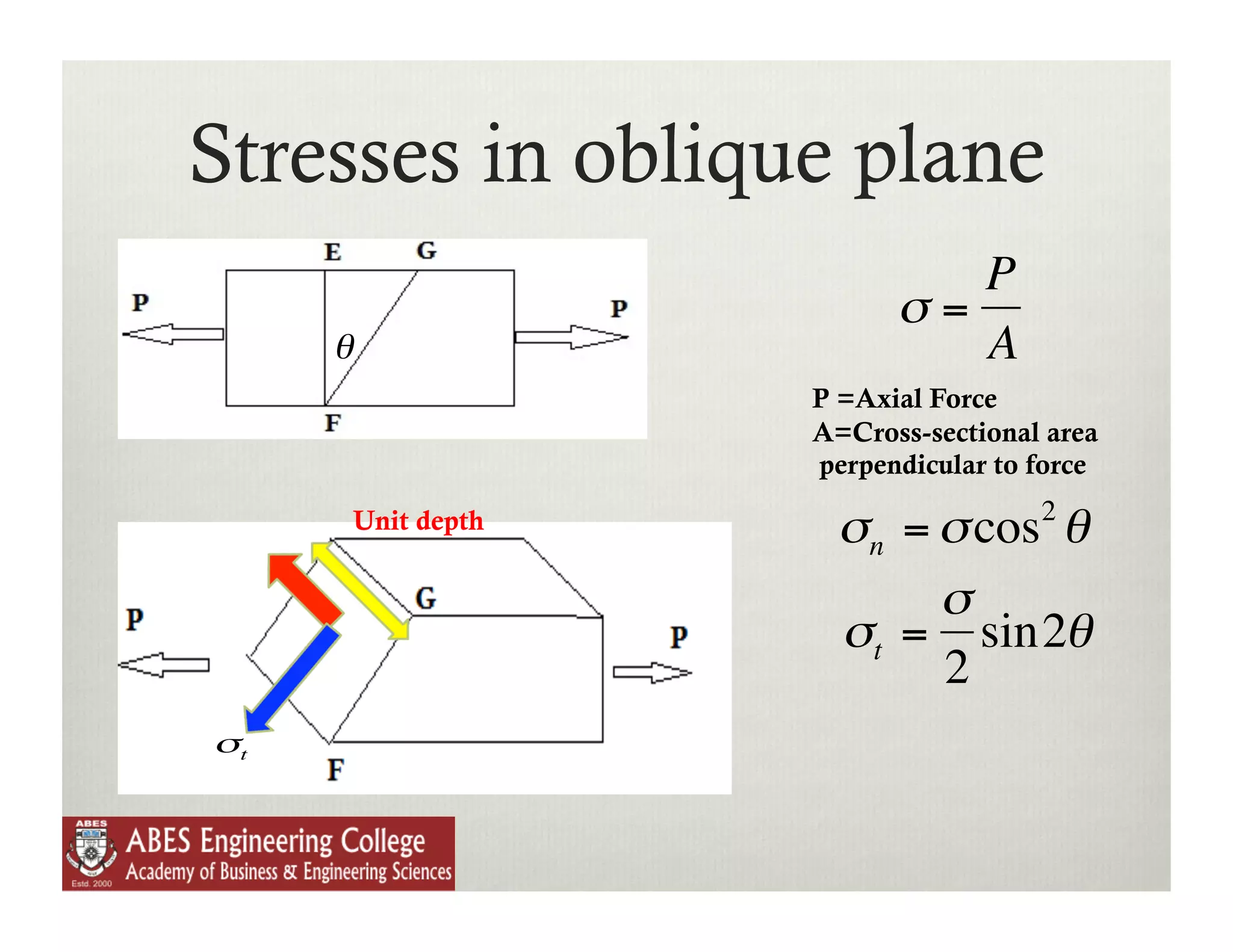
The document discusses various topics related to stress and strain including: principal stresses and strains, Mohr's stress circle theory of failure, 3D stress and strain, equilibrium equations, and impact loading. It provides examples of stresses acting in different planes including normal, shear, oblique, and principal planes. It also gives examples of calculating normal and tangential stresses on an oblique plane subjected to stresses in one, two, or multiple directions with and without shear stresses.
More Related Content
Similar to Lecture 2 principal stress and strain
Lecture 2 principal stress and strain
- 2. Unit 1- Stressand Strain Topics Covered Lecture -1 - Introduction, state of plane stress Lecture -2 - Principle Stresses and Strains Lecture -3 - Mohr's Stress Circle and Theory of Failure Lecture -4- 3-D stress and strain, Equilibrium equations and impact loading Lecture -5 - Generalized Hook's law and Castigliono's
- 3. Stresses and strains In last lecture we looked at stresses were acting in a plane that was at right angles/parallel to the action of force. Tensile Stress Shear Stress
- 4. Stresses and strains Compressive load Failure in shear Stresses are acting normal to the surface yet the material failed in a different plane
- 5. Principal stresses and strains What are principal stresses. Planes that have no shear stress are called as principal planes. Principal planes carry only normal stresses
- 6. Stresses in obliqueplane In real life stresses does not act in normal direction but rather in inclined planes. Normal Plane Oblique Plane
- 7. Stresses in obliqueplane P σ= θ A P =Axial Force A=Cross-sectional area perpendicular to force € 2 σn Unit depth € σn = σ cos θ σ € σt = sin2θ 2 σt € € €
- 8. Stresses in obliqueplane σ1 σ1 Member subjected to direct stress in one plane σ2 € € Member subjected to direct stress in two mutually σ1 σ1 perpendicular plane € σ2 τ € € τ τ Member subjected to simple shear stress. € € τ σ2 € τ € τ Member subjected to direct stress in two σ1 σ1 € mutually perpendicular directions + simple shear τ stress € € τ σ €2 € € € € €
- 9. Stresses in obliqueplane Member subjected to direct stress in two mutually perpendicular directions + simple shear stress σ1 + σ2 σ1 − σ2 σn = + cos2θ + τ sin2θ 2 2 σ1 − σ2 σt = sin2θ − τ cos2θ 2 € €
- 10. Stresses in obliqueplane Member subjected to direct stress in two mutually perpendicular directions + simple shear stress POSITION OF PRINCIPAL PLANES Shear stress should be zero σ1 − σ2 σt = sin2θ − τ cos2θ = 0 2 2τ tan2θ = σ1 − σ2 €
- 11. Stresses in obliqueplane Member subjected to direct stress in two mutually perpendicular directions + simple shear stress POSITION OF PRINCIPAL PLANES 2τ tan2θ = σ1 − σ 2 2τ 2τ sin2θ = 2 (σ1 − σ 2 ) + 4τ 2 θ € cos2θ = (σ1 − σ 2 ) σ1 − σ 2 2 (σ1 − σ 2 ) + 4τ 2 € € € € €
- 12. Stresses in obliqueplane Member subjected to direct stress in two mutually perpendicular directions + simple shear stress 2 σ1 + σ2 ⎛ σ1 − σ2 ⎞ Major principal Stress = + ⎜ ⎟ +τ2 2 ⎝ 2 ⎠ 2 σ1 + σ2 ⎛ σ1 − σ2 ⎞ 2 Minor principal Stress = − ⎜ ⎟ + τ € 2 ⎝ 2 ⎠ €
- 13. Stresses in obliqueplane Member subjected to direct stress in two mutually perpendicular directions + simple shear stress MAX SHEAR STRESS d dθ (σ t ) = 0 d ⎡σ1 − σ 2 ⎤ σ1 − σ 2 ⎢ 2 sin2θ − τ cos2θ ⎥ = 0 tan2θ = dθ ⎣ ⎦ 2τ € € €
- 14. Stresses in obliqueplane Member subjected to direct stress in two mutually perpendicular directions + simple shear stress MAX SHEAR STRESS Evaluate the following equation at σ1 − σ2 σt = sin2θ − τ cos2θ 2 σ1 − σ 2 tan2θ = 2τ 1 2 € (σt )max = 2 (σ1 − σ2 ) + 4τ 2 €
- 15. Stresses in obliqueplane Member subjected to direct stress in one plane Member subjected to direct stress in two mutually perpendicular plane Member subjected to simple shear stress. Member subjected to direct stress in two mutually perpendicular directions + simple shear stress
- 16. Stresses in obliqueplane Member subjected to direct stress in one plane σ1 + σ2 σ1 − σ2 σn = + cos2θ + τ sin2θ 2 2 σ1 − σ2 σt = sin2θ − τ cos2θ 2 Stress in one direction and no shear stress σ2 = 0 τ = 0 € σ1 σ1 σn = + cos2θ = σ1 cos2 θ € 2 2 € σ € 1 σt = sin2θ 2 €
- 17. Stresses in obliqueplane Member subjected to direct stress in two mutually perpendicular plane σ1 + σ2 σ1 − σ2 σn = + cos2θ + τ sin2θ 2 2 σ1 − σ2 σt = sin2θ − τ cos2θ 2 Stress in two direction and no shear stress τ =0 € σ1 + σ2 σ1 − σ2 σn = + cos2θ € 2 2 €σ − σ σt = 1 2 sin2θ 2 €
- 18. Stresses in obliqueplane Member subjected to simple shear stress. σ1 + σ2 σ1 − σ2 σn = + cos2θ + τ sin2θ 2 2 σ1 − σ2 σt = sin2θ − τ cos2θ 2 No stress in axial direction but only shear stress σ1 = σ 2 = 0 € σn = τ sin2θ € σt = € τ cos2θ − € €
- 19. Principal stresses and strains PROBLEM- The tensile stresses at a point across two mutually perpendicular planes are 120N/mm2 and 60 N/mm2. Determine the normal, tangential and resultant stresses on a plane inclined at 30deg to the minor stress.
- 20. Principal stresses and strains PROBLEM- A rectangular block of material is subjected to a tensile stress of 110 N/mm2 on one plane and a tensile stress of 47 N/mm2 on the plane at right angles to the former. Each of the above stresses is accompanied by a shear stress of 63 N/ mm2 and that associated with the former tensile stress tends to rotate the block anticlockwise. Find 1)The direction and magnitude of each of the principal stress. 2) Magnitude of the greatest shear stress.