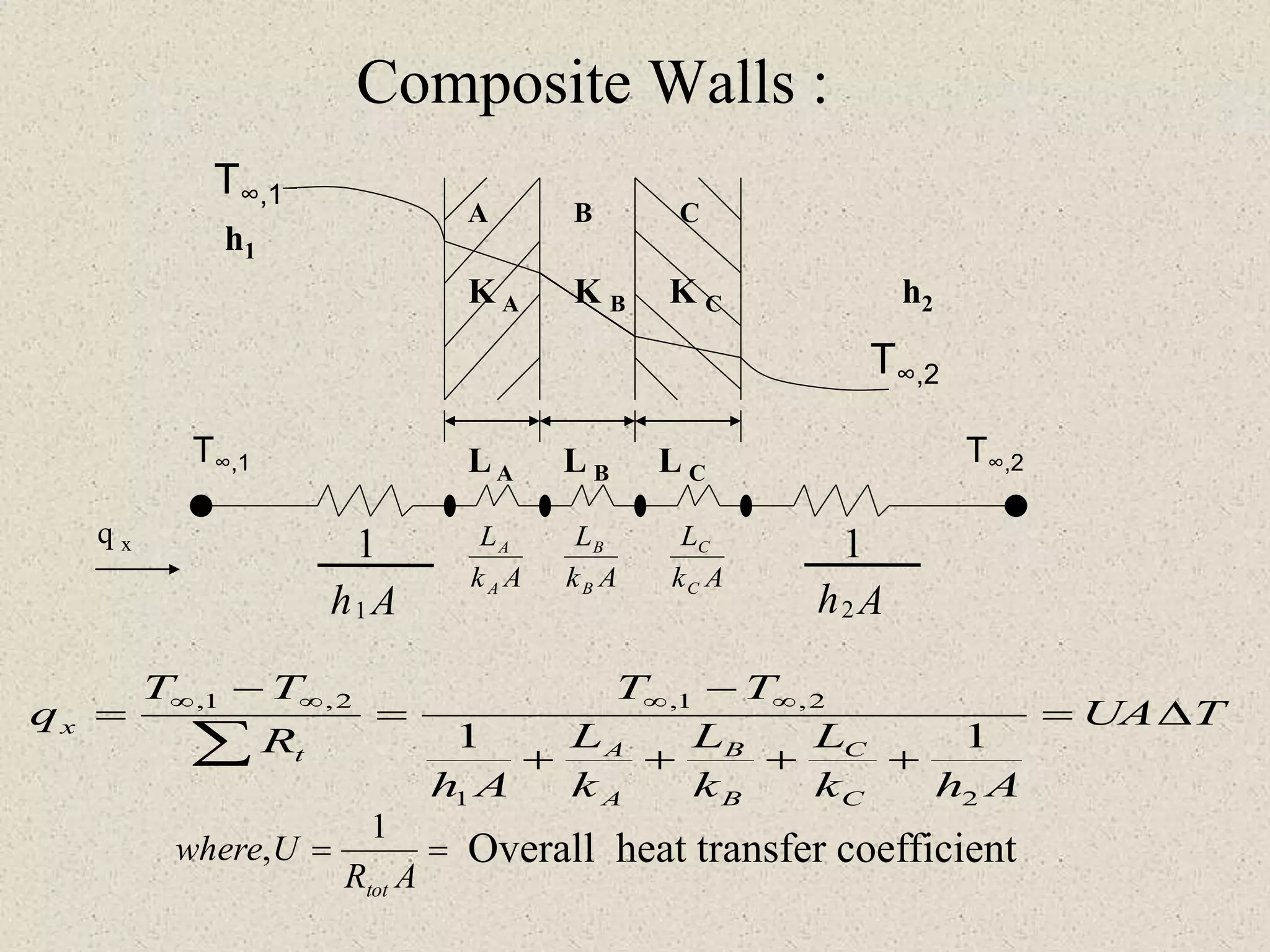
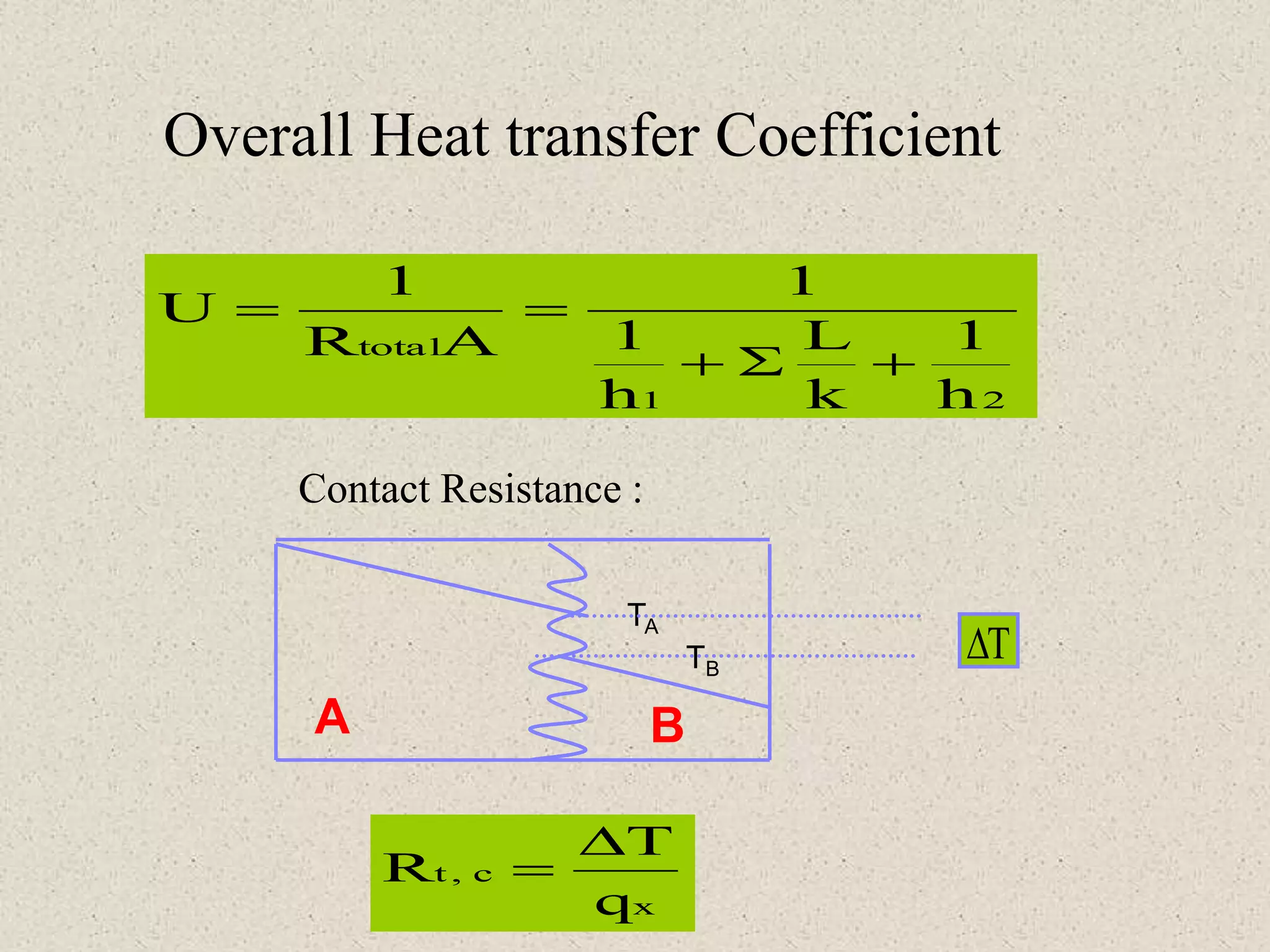
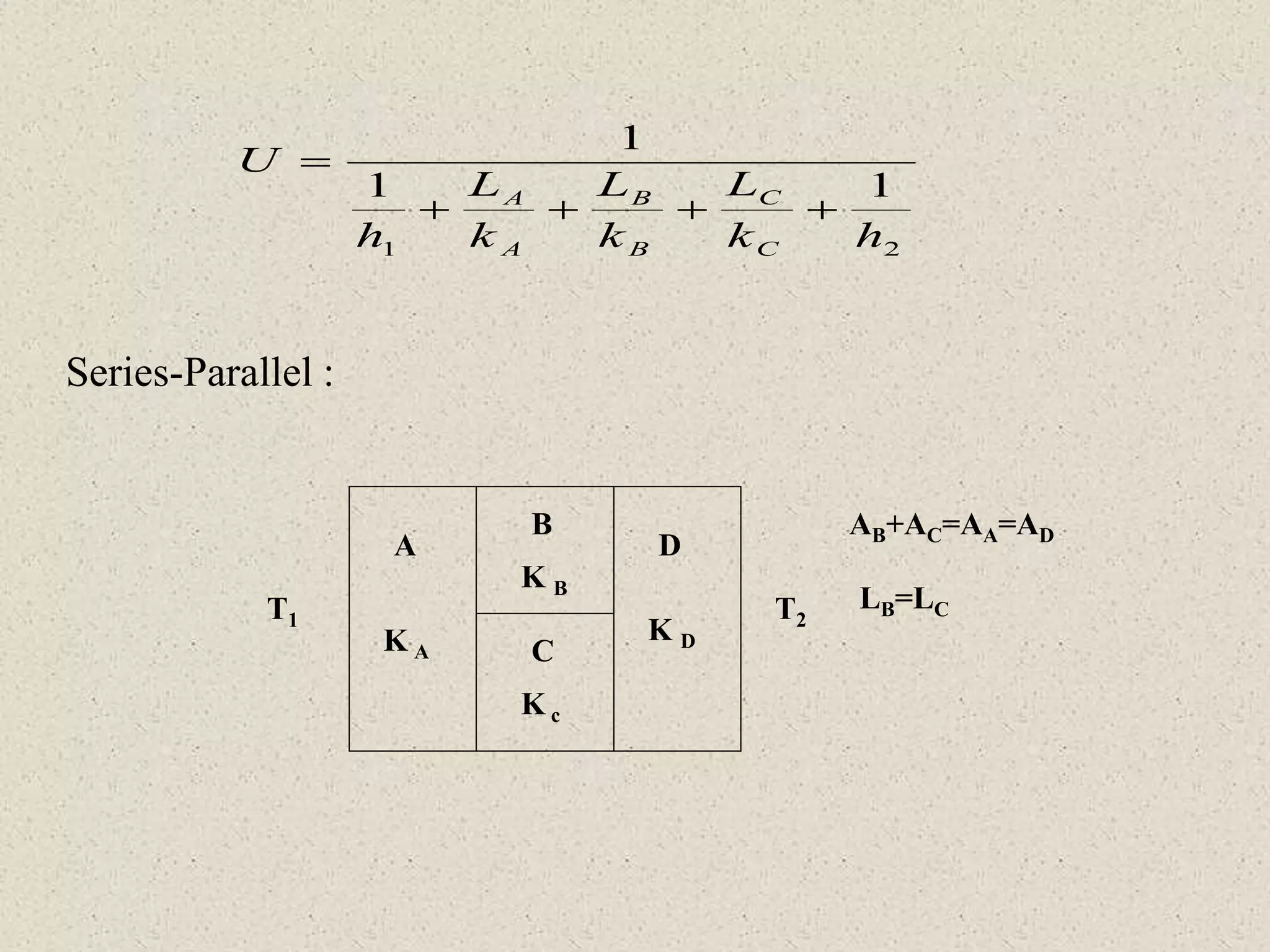
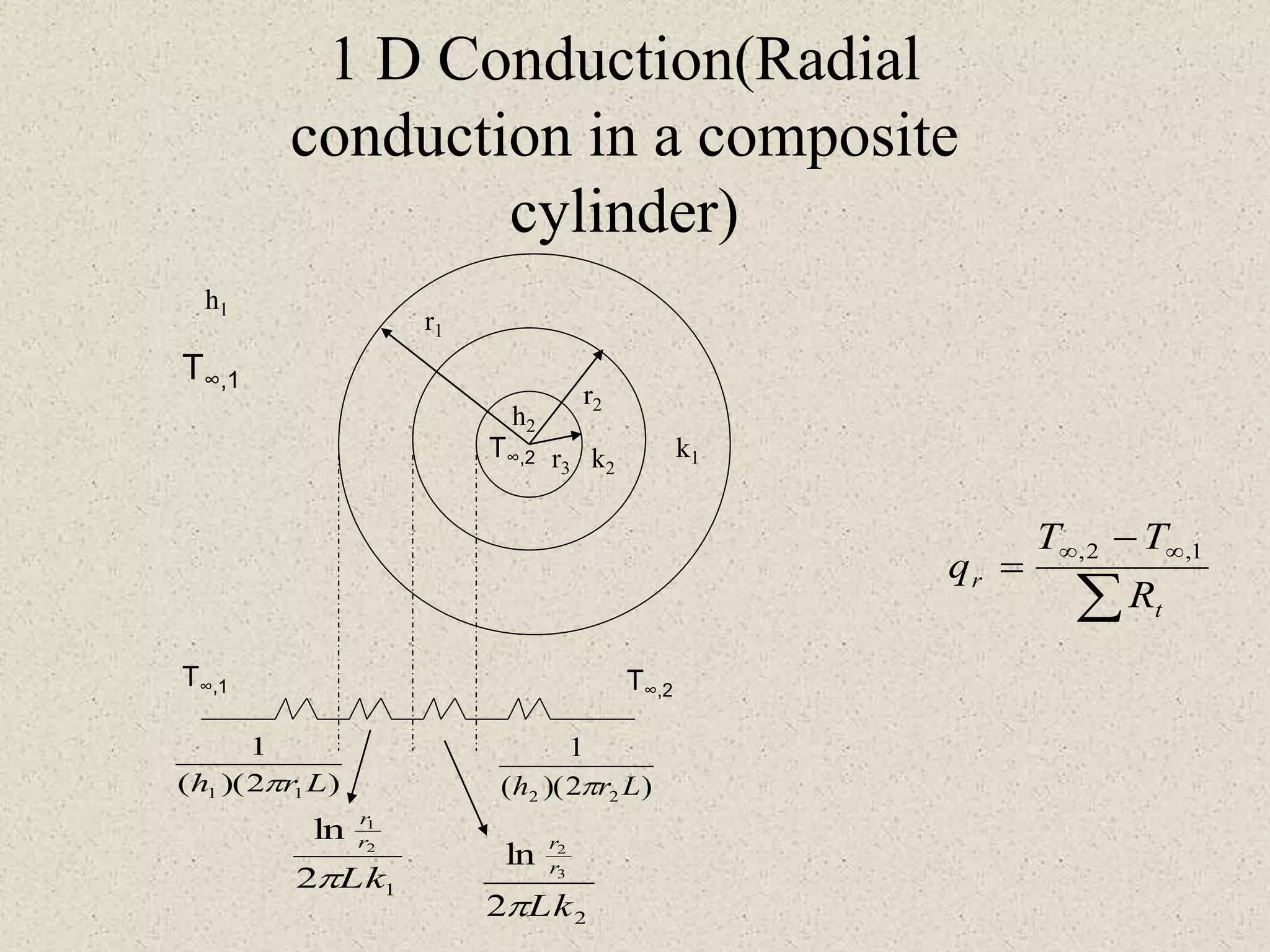
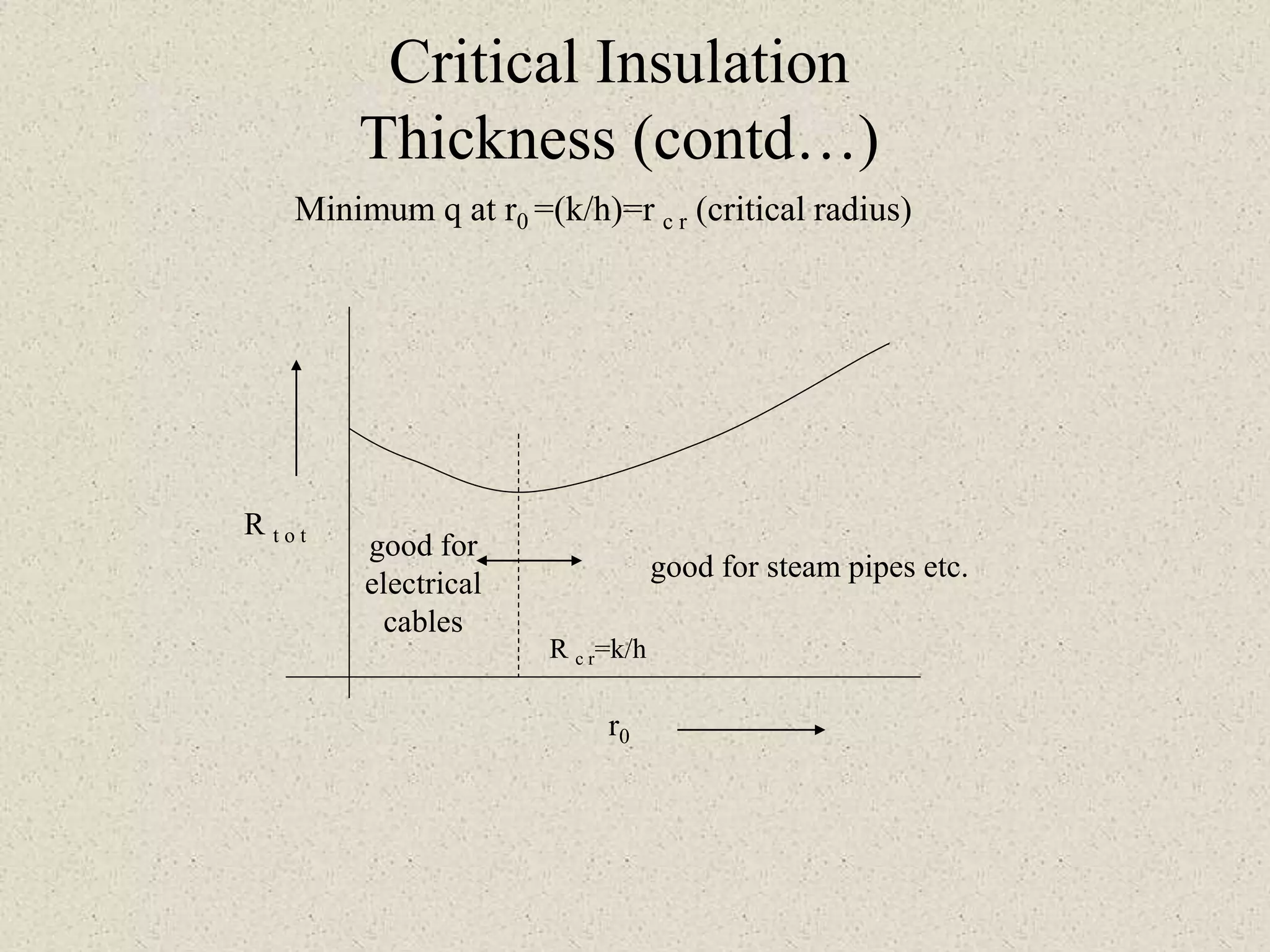
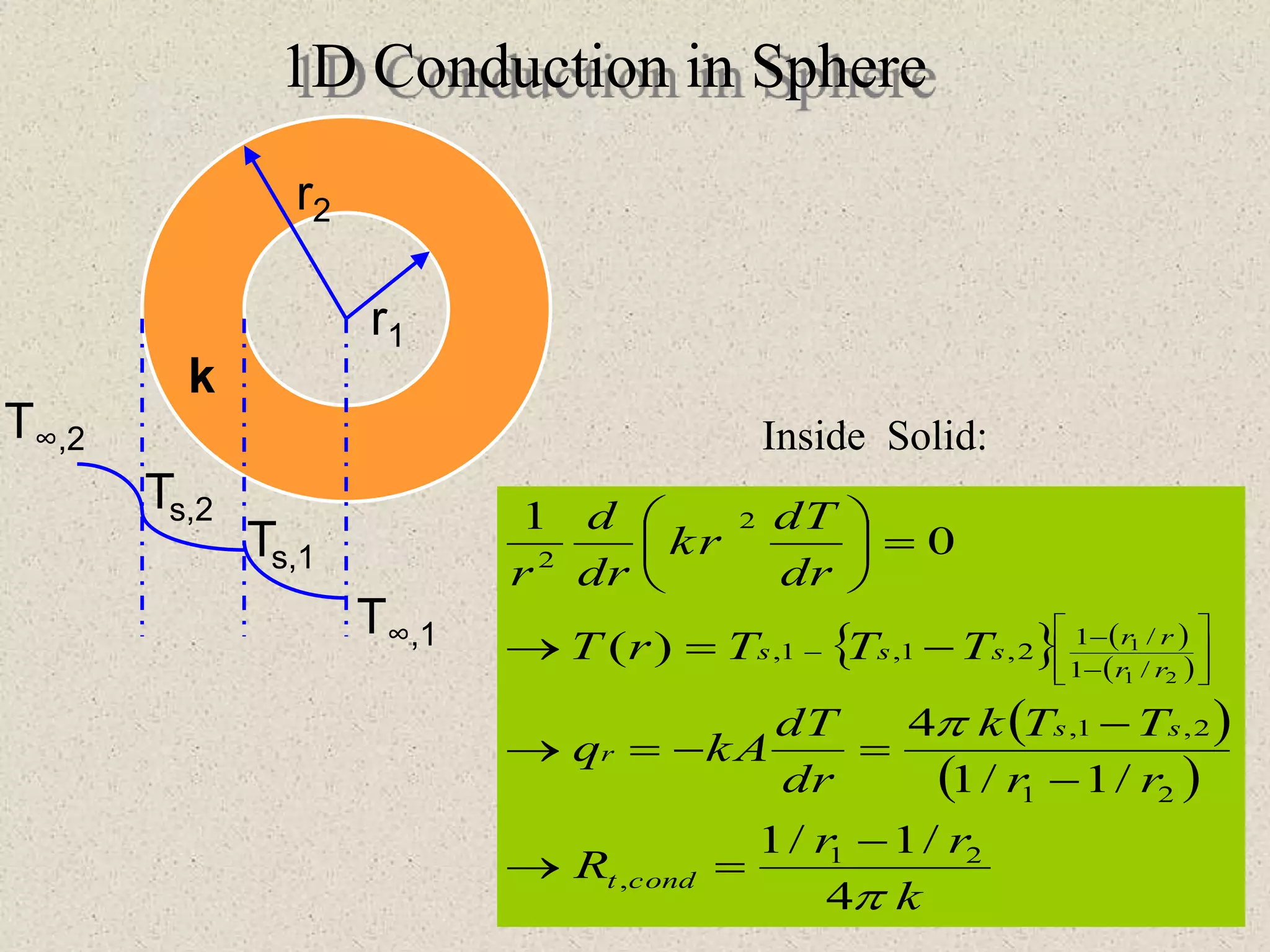
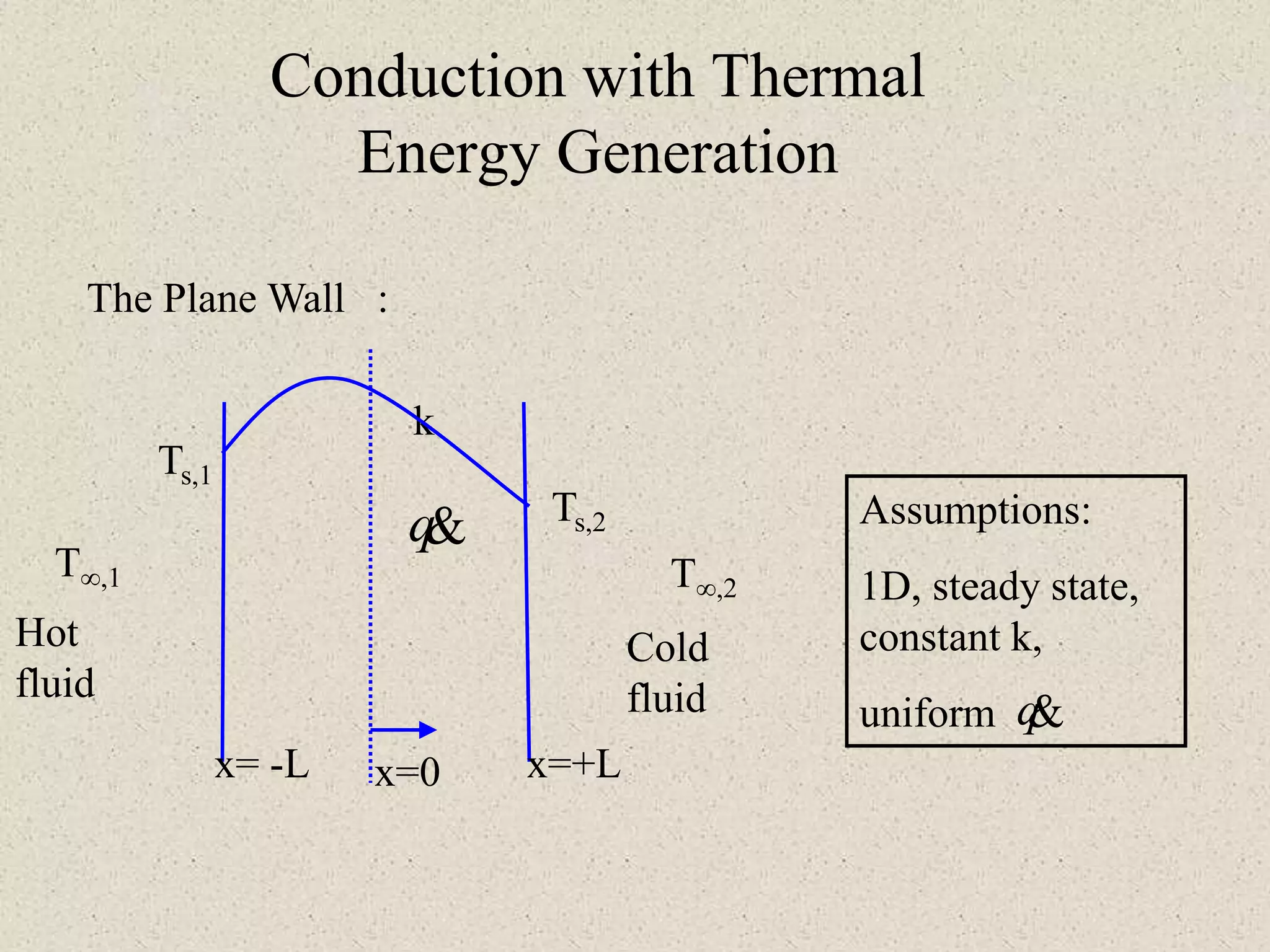
* Given: K=25 W/mK, diameter=3mm, length=1m, R=2 Ω, I=100A * Heat generation per unit volume (q) = I2R = (100A)2 × 2Ω = 20000 W/m3 * Using cylindrical heat conduction equation with internal heat generation and boundary conditions: k(dT/dr) + q = 0 T(r0) = T∞ k(dT/dr)|r=ri = h(T - T∞) Solving the above equations, we get the center temperature Tc.

1. BHEEMANNA KHANDRE INSTITUTE OF TECHNOLOGY, BHALKI
Dept. of Applied Science and Humanities, (Mathematics)
Sub: Engg. Mathematics-III
Sub.code: 15MAT31
Module-3: Partial Differential Equations
by
Dr. Jagadish Tawade
Asst Professor,
BKIT, Bhalki

2. UNIT-3: APPLICATION OF PARTIAL DIFFERENTIALM EQUATION:
Various possible solutions of one dimensional wave and heat equations, two
dimensional Laplace’s equation by the method of separation of variables,
Solution of all these equations with specified boundary conditions. D’Alembert’s
solution of one dimensional wave equation.
[6 hours]

3. Objectives of conduction analysis
To determine the temperature field, T(x,y,z,t), in a body
(i.e. how temperature varies with position within the body)
T(x,y,z,t) depends on:
- boundary conditions
- initial condition
- material properties (k, cp,  …)
- geometry of the body (shape, size)
Why we need T(x,y,z,t) ?
- to compute heat flux at any location (using Fourier’s eqn.)
- compute thermal stresses, expansion, deflection due to temp. etc.
- design insulation thickness
- chip temperature calculation
- heat treatment of metals
T(x,y,z)

4. 0
Area =
A x
x x+x
q= Internal heat generation per unit vol. (W/m3)
qx qx+x
A
Solid bar, insulated on all
long sides (1D heat
conduction)
Unidirectional heat
conduction (1D)

5. Unidirectional heat
conduction (1D)
First Law (energy balance)
t
E
qxAqq xxx


=+- + )(
stgenoutin EEEE  =+- )(
t
T
xcA
t
u
xA
t
E
uxAE


=


=


=

 )(
x
x
q
qq
x
T
kAq
x
xxx
x



+=


-=
+

6. If k is a constant
t
T
t
T
k
c
k
q
x
T


=


=+


a
 1
2
2

Unidirectional heat conduction
(1D)(contd…)
t
T
cq
x
T
k
x
t
T
xAcqxAx
x
T
k
x
A
x
T
kA
x
T
kA


=+











=+









+


+


-




Longitudinal
conduction
Thermal inertiaInternal heat
generation

7. Unidirectional heat conduction
(1D)(contd…)
 For T to rise, LHS must be positive (heat input is
positive)
 For a fixed heat input, T rises faster for higher a
 In this special case, heat flow is 1D. If sides were not
insulated, heat flow could be 2D, 3D.

8. Boundary and Initial conditions:
 The objective of deriving the heat diffusion equation is to
determine the temperature distribution within the conducting
body.
 We have set up a differential equation, with T as the
dependent variable. The solution will give us T(x,y,z).
Solution depends on boundary conditions (BC) and initial
conditions (IC).

9. Boundary and Initial
conditions (contd…)
How many BC’s and IC’s ?
- Heat equation is second order in spatial coordinate. Hence, 2
BC’s needed for each coordinate.
* 1D problem: 2 BC in x-direction
* 2D problem: 2 BC in x-direction, 2 in y-direction
* 3D problem: 2 in x-dir., 2 in y-dir., and 2 in z-dir.
- Heat equation is first order in time. Hence one IC needed

10. 1- Dimensional Heat Conduction
The Plane Wall :
.. .. . . … . .
. . . . .. . . . . .
. . . . . . . . . .
.
.. . . . . . . . .
. .. . . . . . .
. . . . . . .
…. . . . . . .. ..
.. . . . . .. . .. .
. . . .. . . . . . .
. .
k
T∞,2
Ts,1
Ts,2
x=0 x=LHot
fluid
Cold
fluid
0=





dx
dT
k
dx
d
 
kAL
TT
TT
L
kA
dx
dT
kAq
ss
ssx
/
2,1,
2,1,
-
=-=-=
Const. K; solution is:

11. Thermal resistance
(electrical analogy)
OHM’s LAW :Flow of Electricity
V=IR elect
Voltage Drop = Current flow×Resistance

12. Thermal Analogy to Ohm’s
Law :
thermqRT =
Temp Drop=Heat Flow×Resistance

13. 1 D Heat Conduction through a
Plane Wall
qx
T∞,1 Ts,1 Ts,2 T∞,2
Ak
L
Ah2
1
Ah1
1
.. .. . . … . .
. . . . .. . . . . .
. . . . . . . . . .
.
.. . . . . . . . .
. .. . . . . . .
. . . . . . .
…. . . . . . .. ..
.. . . . . .. . .. .
. . . .. . . . . . .
. .
k
T∞,2
Ts,1
Ts,2
x=0 x=L
Hot
fluid
Cold
fluid
T∞,1
 ++=
AhkA
L
Ah
Rt
21
11
(Thermal Resistance )

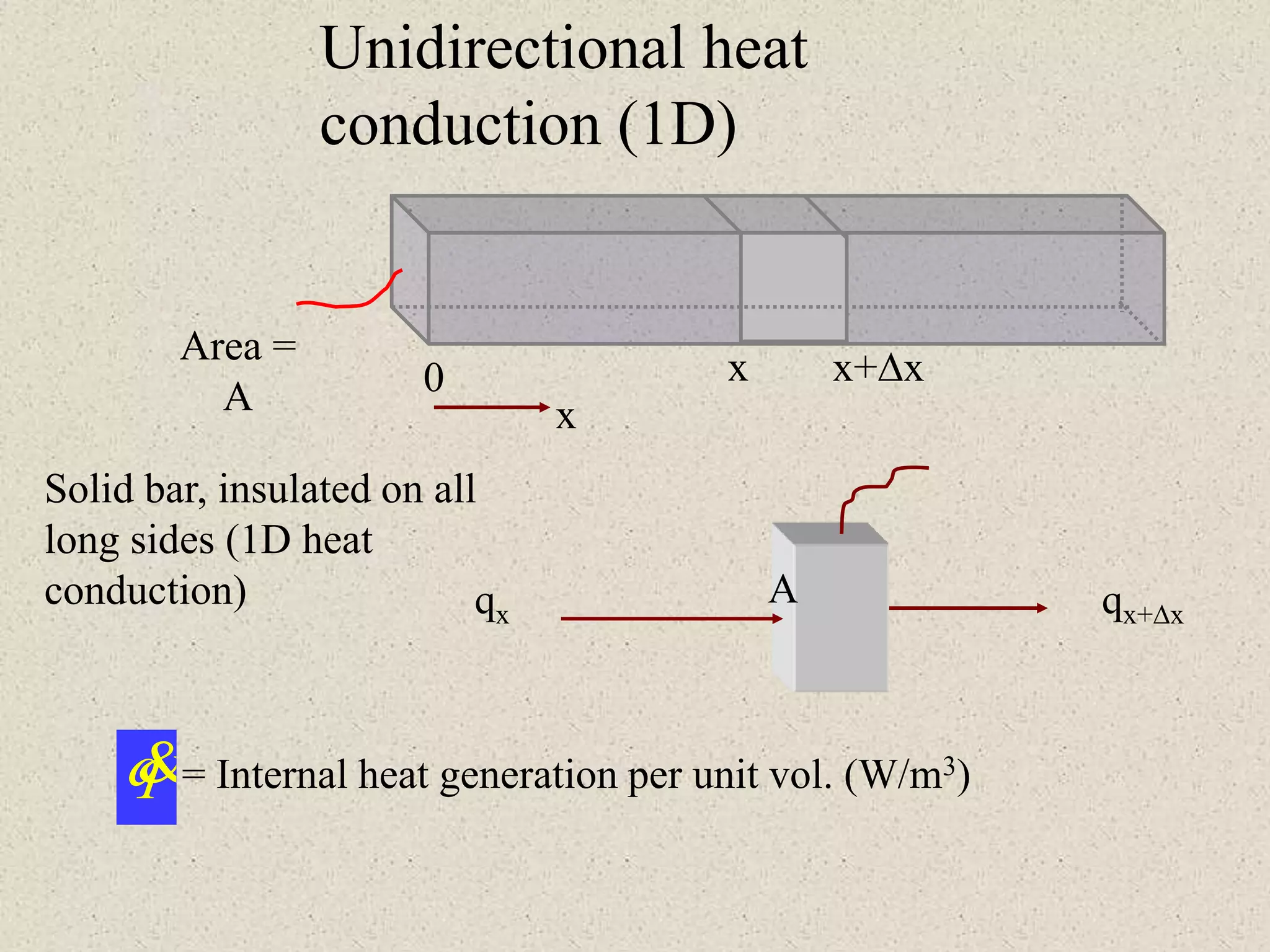
14. Resistance expressions
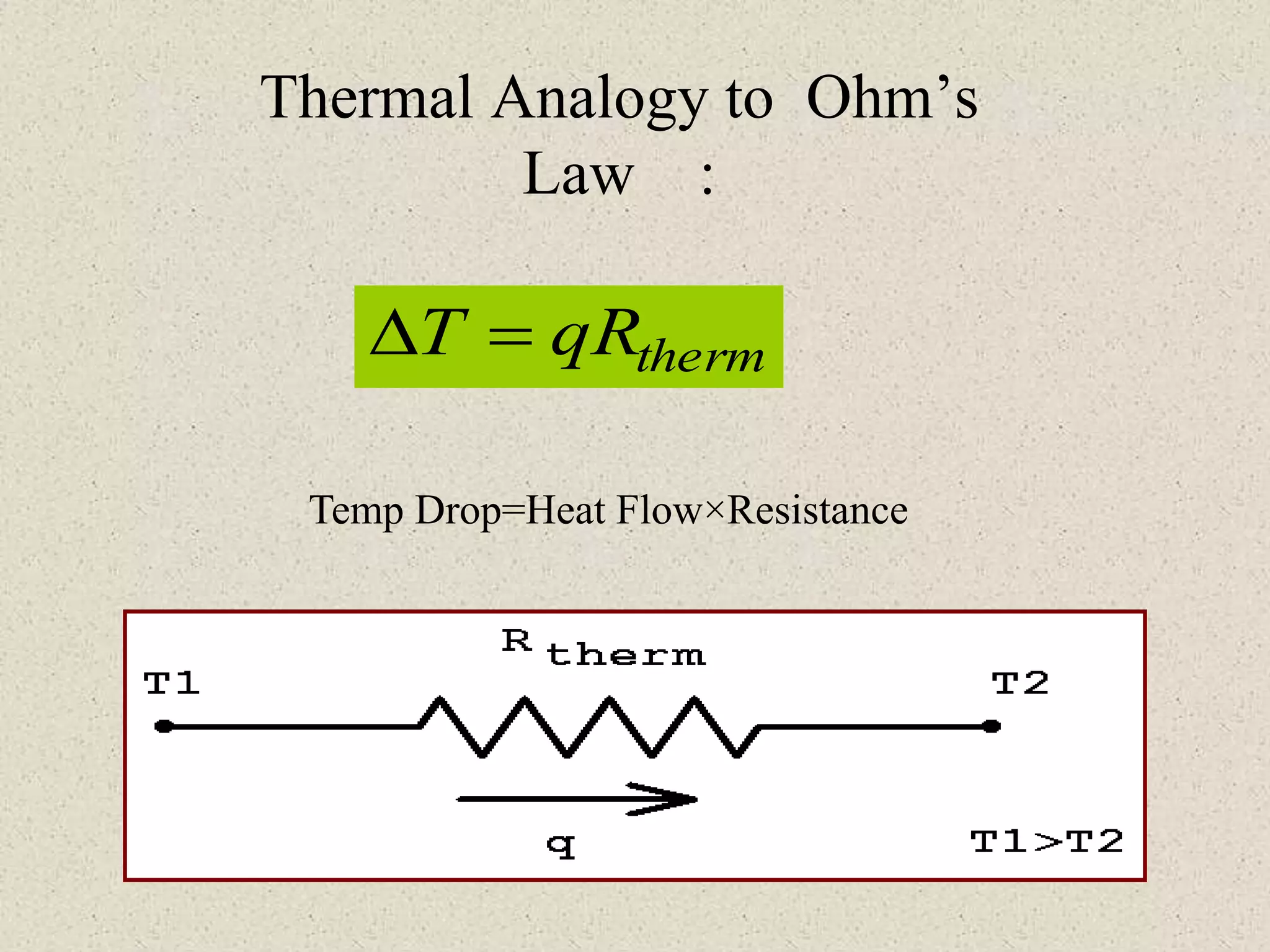
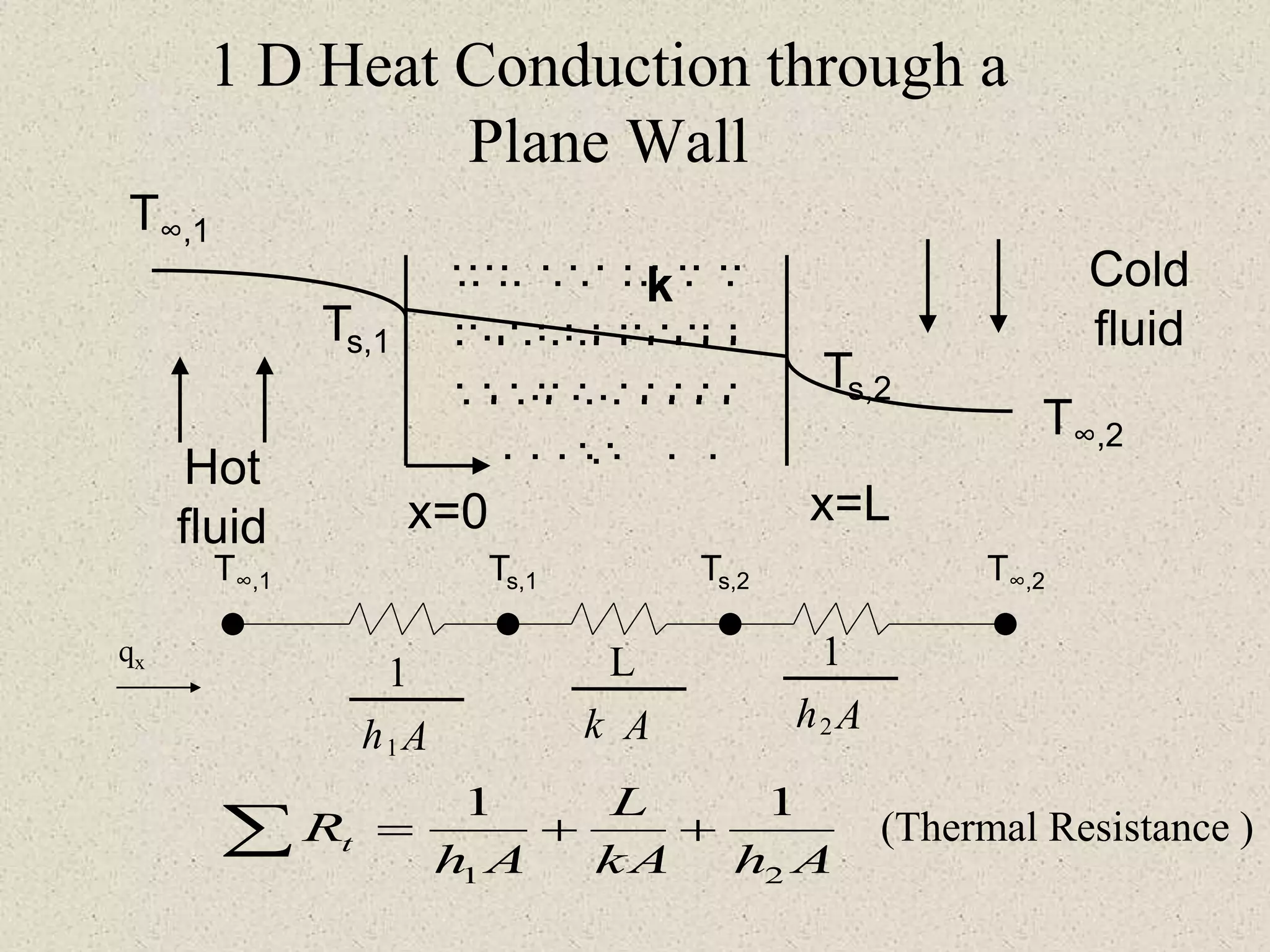
THERMAL RESISTANCES
 Conduction
Rcond = x/kA
 Convection
Rconv = (hA)
-1
 Fins
Rfin = (h
-
 Radiation(aprox)
Rrad = [4AF(T1T2)
1.5
]
-1

15. Composite Walls :
A B C
T∞,1
T∞,2
h1
h2K A K B K C
LA L B L C
q x
T∞,1 T∞,2
Ah1
1
Ah2
1
Ak
L
A
A
Ak
L
B
B
Ak
L
C
C
TUA
Ahk
L
k
L
k
L
Ah
TT
R
TT
q
C
C
B
B
A
At
x =
++++
-
=
-
= 

21
2,1,2,1,
11
==
AR
Uwhere
tot
1
, Overall heat transfer coefficient

16. Overall Heat transfer Coefficient
21
total
h
1
k
L
h
1
1
AR
1
U
++
==
Contact Resistance :
A B
TA
TB
T
x
c,t
q
T
R

=

17. 21
11
1
hk
L
k
L
k
L
h
U
C
C
B
B
A
A
++++
=
Series-Parallel :
A
B
D
C
T1 T2
K c
K DK A
K B
AB+AC=AA=AD
LB=LC

18. Series-Parallel
(contd…)
Assumptions :
(1) Face between B and C is insulated.
(2) Uniform temperature at any face normal to X.
T1
T2
Ak
L
A
A
Ak
L
D
D
Ak
L
B
B
Ak
L
C
C

19. Consider a composite plane wall as shown:
Develop an approximate solution for the rate of heat
transfer through the wall.
Example:
kI = 20 W/mk
AI = 1 m2, L = 1m
kII = 10 W/mk
AII = 1 m2, L = 1m
T1 =
0°C
Tf = 100°C
h = 1000 W/ m2 k
qx

20. 1 D Conduction(Radial
conduction in a composite
cylinder)
h1
T∞,1
k1
r1
r2
k2
T∞,2 r3
h2
T∞,1 T∞,2
)2)((
1
11 Lrh  )2)((
1
22 Lrh 
12
ln 2
1
Lk
r
r

22
ln 3
2
Lk
r
r


 -
=
t
r
R
TT
q
1,2,

21. Critical Insulation
Thickness :
r0
ri
T∞
Ti
h
Insulation Thickness : r o-r i
hLrkL
R ir
r
tot
)2(
1
2
)ln(
0
0

+=
Objective : decrease q , increases
Vary r0 ; as r0 increases ,first term
increases, second term decreases.
totR

22. Critical Insulation
Thickness (contd…)
Set 0
0
=
dr
dRtot
0
2
1
2
1
0
2
0
=-
hLrLkr 
h
k
r =0
Max or Min. ? Take : 0
0
2
2
=
dr
Rd tot at
h
k
r =0
h
k
r
tot
hLrLkrdr
Rd
=
+
-
=
0
0
2
0
2
0
2
2
1
2
1

0
2 3
2
Lk
h

=
Maximum – Minimum problem

23. Minimum q at r0 =(k/h)=r c r (critical radius)
good for steam pipes etc.
good for
electrical
cables
R c r=k/h
r0
R t o t
Critical Insulation
Thickness (contd…)

24. 1D Conduction in Sphere
r1
r2
k
Ts,1
Ts,2
T∞,1
T∞,2
   
 
 
 
k
rr
R
rr
TTk
dr
dT
kAq
TTTrT
dr
dT
kr
dr
d
r
condt
ss
r
rr
rr
sss


4
/1/1
/1/1
4
)(
0
1
21
,
21
2,1,
/1
/1
2,1,1,
2
2
21
1
-
=
-
-
=-=
-=
=













-
-
-
Inside Solid:

25. Applications: * current carrying conductors
* chemically reacting systems
* nuclear reactors
= Energy generation per unit volume
V
E
q

=
Conduction with Thermal
Energy Generation

26. Conduction with Thermal
Energy Generation
The Plane Wall :
k
Ts,1
Ts,2
x=0 x=+L
Hot
fluid
Cold
fluid
T∞,2
T∞,1
x= -L
q Assumptions:
1D, steady state,
constant k,
uniform q

27. Conduction With Thermal
Energy Generation (contd…)
CxCx
k
q
TSolution
TTLx
TTLxcondBoundary
k
q
dx
Td
s
s
++-=
=+=
=-=
=+
2
:
,
,:.
0
21
2
2,
1,
2
2



28. Not linear any more
Derive the expression and show that it is not
independent of x any more
Hence thermal resistance concept is not correct to use when there is internal
heat generation
dx
dT
kqfluxHeat
TT
L
xTT
L
x
k
Lq
TsolutionFinal
CandCfindtoconditionsboundaryUse
x
ssss
-=
+
+
-
+





-=
:
22
1
2
:
1,2,1,2,
2
22
21

Conduction with Thermal
Energy Generation (cont..)

29. Cylinder with heat source
Assumptions:
1D, steady state, constant
k, uniform
Start with 1D heat equation in cylindrical
co-ordinates:
k
q
dr
dT
r
dr
d
r
=+





0
1 
ro
r
Ts
T∞ h
q
q

30. rk
Trcond

==
04
,:.
s
s
T
r
r
q
rTSolution
dr
dT
r
TrBoundary
+





-=
==
2
2
2
0
0
1)(:
0,0

Ts may not be known. Instead, T and h may be specified.
Exercise: Eliminate Ts, using T and h.
Cylinder With Heat Source

31. Cylinder with heat source
(contd…)
Example:
A current of 100A is passed through a stainless steel wire having a
thermal conductivity K=25W/mK, diameter 3mm, and electrical
resistivity R = 2.0 . The length of the wire is 1m. The wire is
submerged in a liquid at 100°C, and the heat transfer coefficient is
10W/m2K. Calculate the centre temperature of the wire at steady
state condition.