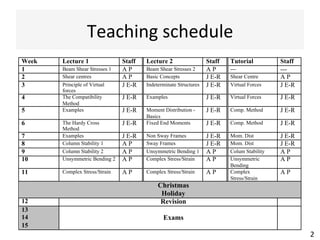
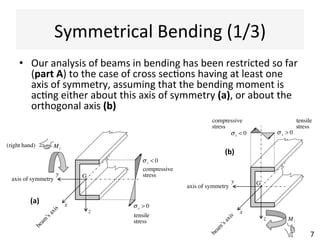
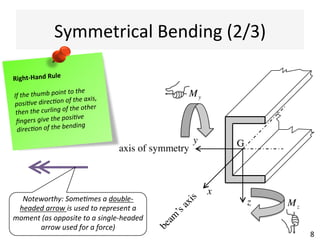
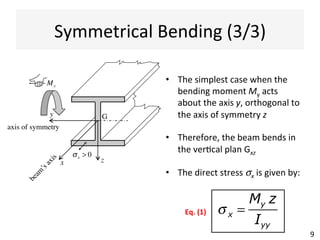
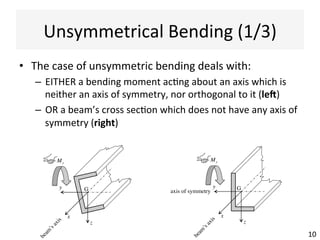
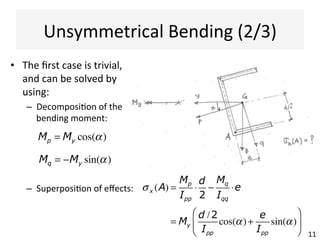
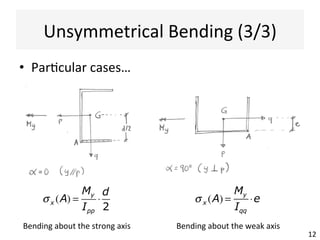
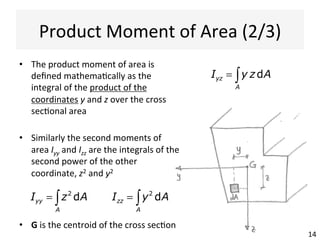
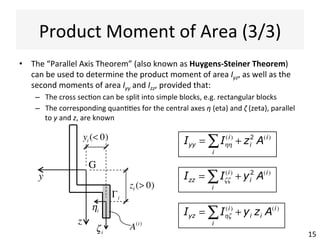
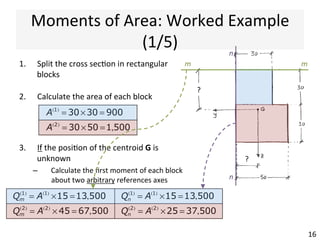
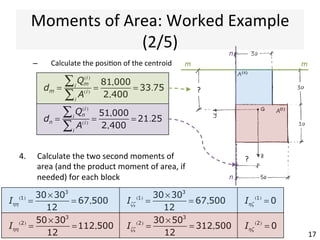
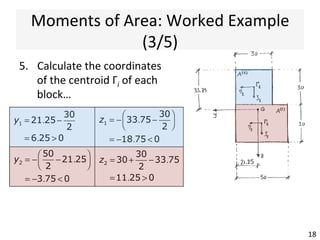
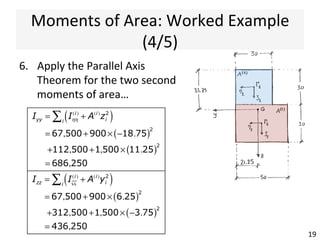
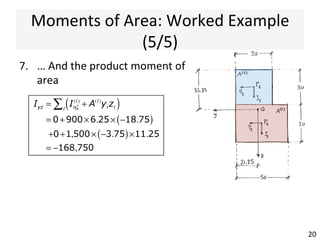
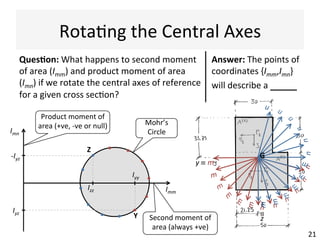
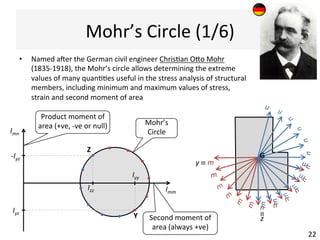
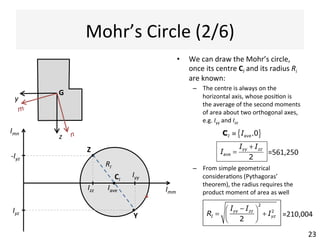
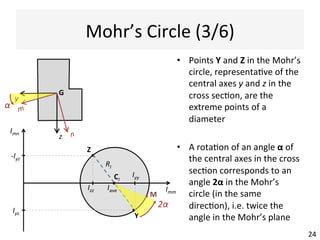
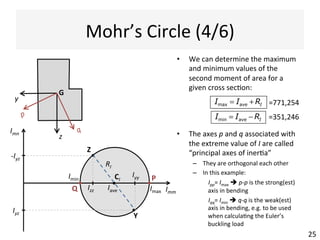
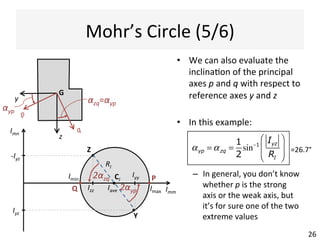
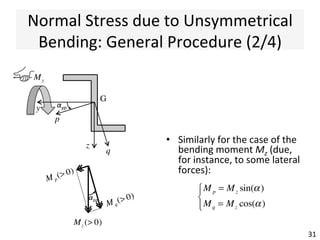
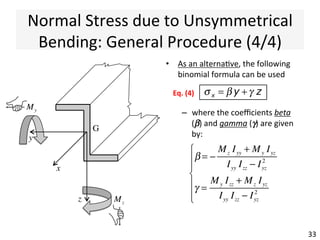
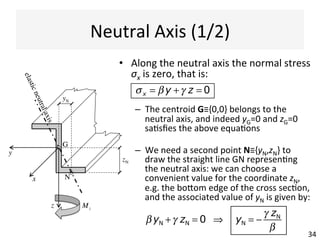
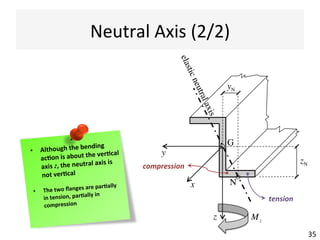
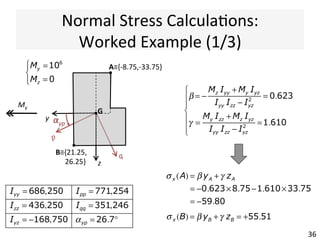
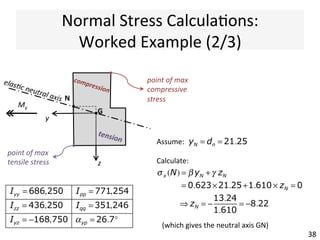
The document outlines a teaching schedule and key concepts related to unsymmetrical bending in structural mechanics, including methods for analyzing shear stresses and principal moments for asymmetric sections. It discusses the theoretical extension of symmetric bending theory to unsymmetrical cases, as well as tools like the Mohr's circle for stress analysis. Learning outcomes include determining principal directional moments and evaluating normal stresses in beams under unsymmetric bending conditions.

1. Unsymmetrical
Bending
Dr
Alessandro
Palmeri
<A.Palmeri@lboro.ac.uk>

2. Teaching
schedule
Week Lecture 1 Staff Lecture 2 Staff Tutorial Staff
1 Beam Shear Stresses 1 A P Beam Shear Stresses 2 A P --- ---
2 Shear centres A P Basic Concepts J E-R Shear Centre A P
3 Principle of Virtual
forces
J E-R Indeterminate Structures J E-R Virtual Forces J E-R
4 The Compatibility
Method
J E-R Examples J E-R Virtual Forces J E-R
5 Examples J E-R Moment Distribution -
Basics
J E-R Comp. Method J E-R
6 The Hardy Cross
Method
J E-R Fixed End Moments J E-R Comp. Method J E-R
7 Examples J E-R Non Sway Frames J E-R Mom. Dist J E-R
8 Column Stability 1 A P Sway Frames J E-R Mom. Dist J E-R
9 Column Stability 2 A P Unsymmetric Bending 1 A P Colum Stability A P
10 Unsymmetric Bending 2 A P Complex Stress/Strain A P Unsymmetric
Bending
A P
11 Complex Stress/Strain A P Complex Stress/Strain A P Complex
Stress/Strain
A P
Christmas
Holiday
12 Revision
13
14 Exams
15
2

3. Mo@va@ons
(1/2)
• Many
cross
sec@ons
used
for
structural
elements
(such
us
Z
sec@ons
or
angle
sec@ons)
do
not
have
any
axis
of
symmetry
• How
does
the
theory
developed
for
symmetrical
bending
can
be
extended
to
such
sec@ons?
3

4. Mo@va@ons
(2/2)
• The
figure
shows
the
finite
element
model
of
a
can@lever
beam
with
Z
cross
sec@on
subjected
to
its
own
weight,
in
which
the
gravita@onal
(ver@cal)
load
induces
lateral
sway
(horizontal),
– exaggerated
for
clarity
• How
can
we
predict
this?
4
XY X
Z
Y
Z
X
Y
X
Z
Y
Z

5. Learning
Outcomes
• When
we
have
completed
this
unit
(2
lectures
+
1
tutorial),
you
should
be
able
to:
– Determine
the
principal
second
moments
of
area
AND
the
principal
direc@ons
of
area
for
unsymmetrical
beam’s
cross
sec@ons
– Evaluate
the
normal
stress
σx
in
beams
subjected
to
unsymmetric
bending
5

6. Further
reading
• R
C
Hibbeler,
“Mechanics
of
Materials”,
8th
Ed,
Pren@ce
Hall
–
Chapter
6
on
“Bending”
• T
H
G
Megson,
“Structural
and
Stress
Analysis”,
2nd
Ed,
Elsevier
–
Chapter
9
on
“Bending
of
Beams”
(eBook)
6

7. Symmetrical
Bending
(1/4)
• Our
analysis
of
beams
in
bending
has
been
restricted
so
far
(part
A)
to
the
case
of
cross
sec@ons
having
at
least
one
axis
of
symmetry,
assuming
that
the
bending
moment
is
ac@ng
either
about
this
axis
of
symmetry
(a),
or
about
the
orthogonal
axis
(b)
7
(a)
x
z
y
axis of symmetry
beam
’saxis
My
G
(right hand)
σ x > 0
σx < 0
tensile
stress
compressive
stress
(b)
x
z
y
axis of symmetry
beam
’saxis
Mz
G
σ x > 0σx < 0
tensile
stress
compressive
stress

8. Symmetrical
Bending
(2/4)
8
x
z
y
axis of symmetry
beam
’saxis
Mz
My
G
Right-­‐Hand
Rule
If
the
thumb
point
to
the
posi0ve
direc0on
of
the
axis,
then
the
curling
of
the
other
fingers
give
the
posi0ve
direc0on
of
the
bending
Noteworthy:
Some0mes
a
double-­‐
headed
arrow
is
used
to
represent
a
moment
(as
opposite
to
a
single-­‐headed
arrow
used
for
a
force)

9. Symmetrical
Bending
(3/4)
9
x
z
y
axis of symmetry
beam
’saxis
My
G
(right hand)
σ x > 0
σx < 0
tensile
stress
compressive
stress
x
z
y
axis of symmetry
beam
’saxis
Mz
G
σ x > 0σx < 0
tensile
stress
compressive
stress
➡
A
posi@ve
bending
moment
My>0,
induces
tensile
stress
σx>0
in
the
boiom
fibres
of
the
cross
sec@on
A
posi@ve
bending
moment
Mz>0,
induces
tensile
stress
σx>0
in
the
right
fibres
of
the
cross
sec@on
(looking
at
it
from
the
posi@ve
direc@on
of
the
x
axis)

10. σ x =
My z
Iyy
Eq.
(1)
Symmetrical
Bending
(4/4)
• The
simplest
case
when
the
bending
moment
My
acts
about
the
axis
y,
orthogonal
to
the
axis
of
symmetry
z
• Therefore,
the
beam
bends
in
the
ver@cal
plan
Gxz
• The
direct
stress
σx
is
given
by:
10
x z
y
axis of symmetry
beam
’saxis
My
σx > 0
G

11. Unsymmetrical
Bending
(1/3)
11
• The
case
of
unsymmetric
bending
deals
with:
– EITHER
a
bending
moment
ac@ng
about
an
axis
which
is
neither
an
axis
of
symmetry,
nor
orthogonal
to
it
(le9)
– OR
a
beam’s
cross
sec@on
which
does
not
have
any
axis
of
symmetry
(right)
x
z
y
beam
’saxis
My
G
x
z
y
axis of symmetry
beam
’saxis
My
G

12. Unsymmetrical
Bending
(2/3)
12
• The
first
case
is
trivial,
and
can
be
solved
by
using:
– Decomposi@on
of
the
bending
moment:
– Superposi@on
of
effects:
Mp = My cos(α)
Mq = −My sin(α)
σx (A) =
Mp
Ipp
⋅
d
2
−
Mq
Iqq
⋅e
= My
d /2
Ipp
cos(α)+
e
Ipp
sin(α)
⎛
⎝
⎜
⎞
⎠
⎟

13. Unsymmetrical
Bending
(3/3)
13
• Par@cular
cases…
Bending
about
the
strong
axis
σx (A) =
My
Ipp
⋅
d
2
Bending
about
the
weak
axis
σ x (A) =
My
Iqq
⋅e

14. Product
Moment
of
Area
(1/3)
14
• Let’s
introduce
a
new
quan@ty,
Iyz,
called
“Product
Moment
of
Area”
– Defined
as:
• If
and
only
if
Iyz
=0,
a
bending
moment
ac@ng
on
one
of
these
two
axes
will
cause
the
beam
to
bend
about
the
same
axis
only,
not
about
the
orthogonal
axis
(symmetric
bending)
– I.e.
a
ver@cal
transverse
load
will
not
induce
any
lateral
sway
and
a
lateral
transverse
will
not
cause
any
ver@cal
movement
= ∫ dyz
A
I y z A

15. Product
Moment
of
Area
(2/3)
15
• The
product
moment
of
area
is
defined
mathema@cally
as
the
integral
of
the
product
of
the
coordinates
y
and
z
over
the
cross
sec@onal
area
• Similarly
the
second
moments
of
area
Iyy
and
Izz
are
the
integrals
of
the
second
power
of
the
other
coordinate,
z2
and
y2
• G
is
the
centroid
of
the
cross
sec@on
Iyy = z2
dA
A
∫ Izz = y2
dA
A
∫
Iyz = y zdA
A
∫

16. Product
Moment
of
Area
(3/3)
16
• The
“Parallel
Axis
Theorem”
(also
known
as
Huygens-­‐Steiner
Theorem)
can
be
used
to
determine
the
product
moment
of
area
Iyz,
as
well
as
the
second
moments
of
area
Iyy
and
Izz,
provided
that:
– The
cross
sec@on
can
be
split
into
simple
blocks,
e.g.
rectangular
blocks
– The
corresponding
quan@@es
for
the
central
axes
η
(eta)
and
ζ
(zeta),
parallel
to
y
and
z,
are
known
Iyy = Iηη
(i)
+ zi
2
A(i)
i
∑
Izz = Iζζ
(i)
+ yi
2
A(i)
i
∑
Iyz = Iηζ
(i)
+ yi zi A(i)
i
∑z
y
G
ηi
ζi
Γi
A(i)
yi (< 0)
zi (> 0)

17. Moments
of
Area:
Worked
Example
(1/5)
17
1. Split
the
cross
sec@on
in
rectangular
blocks
2. Calculate
the
area
of
each
block
3. If
the
posi@on
of
the
centroid
G
is
unknown
– Calculate
the
first
moment
of
each
block
about
two
arbitrary
references
axes
A(1)
= 30×30 = 900
A(2)
= 30×50 =1,500
Qm
(1)
= A(1)
×15 =13,500 Qn
(1)
= A(1)
×15 =13,500
Qm
(2)
= A(2)
× 45 = 67,500 Qn
(2)
= A(2)
×25 = 37,500
?
?
m m
n
n

18. Moments
of
Area:
Worked
Example
(2/5)
18
– Calculate
the
posi@on
of
the
centroid
4. Calculate
the
two
second
moments
of
area
(and
the
product
moment
of
area,
if
needed)
for
each
block
dm =
Qm
(i)
i∑
A(i)
i∑
=
81,000
2,400
= 33.75
dn =
Qn
(i)
i∑
A(i)
i∑
=
51,000
2,400
= 21.25
Iηη
(1)
=
30×303
12
= 67,500 Iζζ
(1)
=
30×303
12
= 67,500 Iηζ
(1)
= 0
Iηη
(2)
=
50×303
12
=112,500 Iζζ
(2)
=
30×503
12
= 312,500 Iηζ
(2)
= 0
m m
n
n
?
?

19. Moments
of
Area:
Worked
Example
(3/5)
19
5. Calculate
the
coordinates
of
the
centroid
Γi
of
each
block…
y1 = 21.25−
30
2
= 6.25 > 0
z1 = − 33.75−
30
2
⎛
⎝⎜
⎞
⎠⎟
= −18.75 < 0
y2 = −
50
2
−21.25
⎛
⎝⎜
⎞
⎠⎟
= −3.75 < 0
z2 = 30+
30
2
−33.75
=11.25 > 0

20. Moments
of
Area:
Worked
Example
(4/5)
20
6. Apply
the
Parallel
Axis
Theorem
for
the
two
second
moments
of
area…
Iyy = Iηη
(i)
+ A(i)
zi
2
( )i∑
= 67,500+900× −18.75( )2
+112,500+1,500× 11.25( )2
= 686,250
Izz = Iζζ
(i)
+ A(i)
yi
2
( )i∑
= 67,500+900× 6.25( )2
+312,500+1,500× −3.75( )2
= 436,250

21. Moments
of
Area:
Worked
Example
(5/5)
21
7. …
And
the
product
moment
of
area
Iyz = Iηζ
(i)
+ A(i)
yi zi( )i∑
= 0+900×6.25× −18.75( )
+0+1,500× −3.75( )×11.25
= −168,750

22. Rota@ng
the
Central
Axes
22
QuesBon:
What
happens
to
second
moment
of
area
(Imm)
and
product
moment
of
area
(Imn)
if
we
rotate
the
central
axes
of
reference
for
a
given
cross
sec@on?
m
n
m
n
m
n
m
n
m
n
m
n
Imm
Imn
Y
Z
Product
moment
of
area
(+ve,
-­‐ve
or
null)
Second
moment
of
area
(always
+ve)
Iyy
Iyz
-­‐Iyz
Izz
Mohr’s
Circle
G
y
≡
≡
z
Answer:
The
points
of
coordinates
{Imm,Imn}
will
describe
a
circle

23. Mohr’s
Circle
(1/6)
23
• Named
aser
the
German
civil
engineer
Chris@an
Oio
Mohr
(1835-­‐1918),
the
Mohr’s
circle
allows
determining
the
extreme
values
of
many
quan@@es
useful
in
the
stress
analysis
of
structural
members,
including
minimum
and
maximum
values
of
stress,
strain
and
second
moment
of
area
m
n
m
n
m
n
m
n
m
n
m
n
Imm
Imn
Y
Z
Product
moment
of
area
(+ve,
-­‐ve
or
null)
Second
moment
of
area
(always
+ve)
Iyy
Iyz
-­‐Iyz
Izz
Mohr’s
Circle
G
y
≡
≡
z

24. Mohr’s
Circle
(2/6)
24
• We
can
draw
the
Mohr’s
circle,
once
its
centre
CI
and
its
radius
Ri
are
known:
– The
centre
is
always
on
the
horizontal
axis,
whose
posi@on
is
the
average
of
the
second
moments
of
area
about
two
orthogonal
axes,
e.g.
Iyy
and
Izz
– From
simple
geometrical
considera@ons
(Pythagoras’
theorem),
the
radius
requires
the
product
moment
of
area
as
well
Imm
Imn
Y
Z
Iyy
Iyz
-­‐Iyz
Izz
y
z
G
m
n CI ≡ Iave,0{ }
Iave =
Iyy + Izz
2
RI =
Iyy − Izz
2
⎛
⎝⎜
⎞
⎠⎟
2
+ Iyz
2
CI
Iave
RI
=561,250
=210,004

25. Mohr’s
Circle
(3/6)
25
• Points
Y
and
Z
in
the
Mohr’s
circle,
representa@ve
of
the
central
axes
y
and
z
in
the
cross
sec@on,
are
the
extreme
points
of
a
diameter
• A
rota@on
of
an
angle
α
of
the
central
axes
in
the
cross
sec@on
corresponds
to
an
angle
2α
in
the
Mohr’s
circle
(in
the
same
direc@on),
i.e.
twice
the
angle
in
the
Mohr’s
plane
Imm
Imn
Iyy
Iyz
-­‐Iyz
Izz
y
z
G
m
n
Y
Z
CI
Iave
RI
α
2α
M

26. Mohr’s
Circle
(4/6)
26
• We
can
determine
the
maximum
and
minimum
values
of
the
second
moment
of
area
for
a
given
cross
sec@on:
• The
axes
p
and
q
associated
with
the
extreme
value
of
I
are
called
“principal
axes
of
iner@a”
– They
are
orthogonal
each
other
– In
this
example:
Ipp=
Imax
è
p-­‐p
is
the
strong(est)
axis
in
bending
Iqq=
Imin
è
q-­‐q
is
the
weak(est)
axis
in
bending,
e.g.
to
be
used
when
calcula@ng
the
Euler’s
buckling
load
Imm
Imn
Y
Z
Iyy
Iyz
-­‐Iyz
Izz
y
z
G
CI
Iave
RI
Imin = Iave − RI
Imax = Iave + RI
Q
Imin
P
Imax
=771,254
=351,246

27. Mohr’s
Circle
(5/6)
27
• We
can
also
evaluate
the
inclina@on
of
the
principal
axes
p
and
q
with
respect
to
reference
axes
y
and
z
• In
this
example:
– In
general,
you
don’t
know
whether
p
is
the
strong
axis
or
the
weak
axis,
but
it’s
for
sure
one
of
the
two
extreme
values
Imm
Imn
Y
Z
Iyy
Iyz
-­‐Iyz
Izz
y
z
G
CI
Iave
RI
αyp = αzq =
1
2
sin−1
Iyz
RI
⎛
⎝
⎜
⎜
⎞
⎠
⎟
⎟
Q
Imin
P
Imax
αyp
αzq=αyp
2αyp
2αzq
=26.7°

28. Mohr’s
Circle
(6/6)
28
• For
any
beam’s
cross
sec@on,
the
principal
axes
p
and
q
always
sa@sfy
the
mathema@cal
condi@on
– That
is,
their
representa@ve
points
P
and
Q
in
the
Mohr’s
circle
belong
to
the
horizontal
axis
• An
axis
of
symmetry
is
always
a
principal
axis
of
the
area
Imm
Imn
Y
Z
Iyy
Iyz
-­‐Iyz
Izz
y
z
G
CI
Iave
RI
Q
Imin
P
Imax
αyp
αzq=αyp
2αyp
2αzq
Ipq = 0

29. Mohr’s
Circle:
Par@cular
Cases
• If
for
a
given
cross
sec@on
Imin=Imax,
then
all
the
central
axes
m
will
have
the
same
second
moment
of
area,
i.e.
Imm=Imin=Imax,
and
all
the
central
axes
m
will
be
principal
axes
of
area,
i.e.
Imn=0
– This
is
the
case,
for
instance,
of
both
circular
and
square
shapes
– The
neutral
axis
(where
σx=0)
will
always
coincide
with
the
axis
about
which
the
bending
moment
is
applied
29
z
y G
x
Mm
m
m
z
y G
x
Mm
m
m

30. Bending
about
Principal
Axes
• In
general,
a
bending
moment
Mp
ac@ng
about
the
principal
axis
p
will
cause
the
beam
to
bend
in
the
orthogonal
Gxq
plane
• The
simple
formula
of
direct
stress
σx
due
to
pure
bending
can
be
resorted
to:
– Similar
to
Eq.
(1)
30
x
beam
’s axis
G
q
p
M p
principal axis
σ x > 0
σx < 0
tensile
stress
compressive
stress
σx =
Mp q
Ipp
Eq.
(2)
Distance
(with
sign)
to
the
neutral
axis

31. Normal
Stress
due
to
Unsymmetrical
Bending:
General
Procedure
(1/4)
• If
the
bending
does
not
act
along
one
of
the
principal
axis
(p
and
q),
then
the
bending
moment
can
be
decomposed
along
the
principal
axes
• In
the
figure,
My
is
the
bending
moment
about
the
horizontal
axis
(due,
for
instance,
to
the
dead
load):
31
My
z
y
G
q
p
ααyp
Mp = My cos(α)
Mq = −My sin(α)
⎧
⎨
⎪
⎩⎪
My (> 0)
M p
(> 0)
M q
(< 0)
ααyp

32. Normal
Stress
due
to
Unsymmetrical
Bending:
General
Procedure
(2/4)
• If
the
bending
does
not
act
along
one
of
the
principal
axis
(p
and
q),
then
the
bending
moment
can
be
decomposed
along
the
principal
axes
• Similarly
for
the
case
of
the
bending
moment
Mz
(due,
for
instance,
to
some
lateral
forces):
32
My
z
y
G
q
p
ααyp
M p = Mz sin(α)
Mq = Mz cos(α)
⎧
⎨
⎪
⎩⎪
M p
(> 0)
α
Mz (> 0)
M q
(> 0)αzq

33. Normal
Stress
due
to
Unsymmetrical
Bending:
General
Procedure
(3/4)
• Once
Mp
and
Mq
are
known,
the
normal
stress
σx
(+ve
in
tension)
can
be
computed
with
the
expression:
33
My
z
y
G
q
p
ααyp
p
and
q
here
are
the
distances
from
the
principal
axes
of
the
point
where
the
stress
σx
is
sought
q
p
G
σ x
q
p
x
σ x =
Mp q
Ipp
−
Mq p
Iqq
Eq.
(3)

34. Normal
Stress
due
to
Unsymmetrical
Bending:
General
Procedure
(4/4)
• As
an
alterna@ve,
the
following
binomial
formula
can
be
used
– where
the
coefficients
beta
(β)
and
gamma
(γ)
are
given
by:
Mz
z
G
My
y
x
σ x = β y +γ z
β = −
Mz Iyy + My Iyz
Iyy Izz − Iyz
2
γ =
My Izz + Mz Iyz
Iyy Izz − Iyz
2
⎧
⎨
⎪
⎪
⎩
⎪
⎪
34
Eq.
(4)

35. Neutral
Axis
(1/2)
• Along
the
neutral
axis
the
normal
stress
σx
is
zero,
that
is:
– The
centroid
G≡{0,0}
belongs
to
the
neutral
axis,
and
indeed
yG=0
and
zG=0
sa@sfies
the
above
equa@ons
– We
need
a
second
point
N≡{yN,zN}
to
draw
the
straight
line
GN
represen@ng
the
neutral
axis:
we
can
choose
a
convenient
value
for
the
coordinate
zN,
e.g.
the
boiom
edge
of
the
cross
sec@on,
and
the
associated
value
of
yN
is
given
by:
z
G
y
x
Mz
N
zN
yN
elasticneutralaxis
σx = β y +γ z = 0
β yN +γ zN = 0 ⇒ yN = −
γ zN
β
35

36. Neutral
Axis
(2/2)
z
G
y
x
Mz
N
zN
yN
elasticneutralaxis
• Although
the
bending
acBon
is
about
the
verBcal
axis
z,
the
neutral
axis
is
not
verBcal
• The
two
flanges
are
parBally
in
tension,
parBally
in
compression
tension
compression
36

37. Normal
Stress
Calcula@ons:
Worked
Example
(1/3)
37
37
y
z
G
αyp
A≡{-­‐8.75,-­‐33.75}
B≡{21.25,
26.25}
My
My =106
Mz = 0
⎧
⎨
⎪
⎩⎪
Iyy = 686,250 Ipp = 771,254
Izz = 436,250 Iqq = 351,246
Iyz = −168,750 αyp = 26.7°
β = −
Mz Iyy + My Iyz
Iyy Izz − Iyz
2
= 0.623
γ =
My Izz + Mz Iyz
Iyy Izz − Iyz
2
=1.610
⎧
⎨
⎪
⎪
⎩
⎪
⎪
σx (A) = β yA +γ zA
= −0.623×8.75−1.610×33.75
= −59.80
σ x (B) = β yB +γ zB = +55.51

38. Normal
Stress
Calcula@ons:
Worked
Example
(2/3)
38
38
y
z
G
αyp
My
Iyy = 686,250 Ipp = 771,254
Izz = 436,250 Iqq = 351,246
Iyz = −168,750 αyp = 26.7°
Mp = My cos(αyp ) = 893,092
Mz = −My sin(αyp ) = −449,874
⎧
⎨
⎪
⎩⎪
σ x (A) =
Mp qA
Ipp
−
Mq pA
Iqq
=
894,092× (−23.00)
771,254
−
(−449,874)× (−26.21)
351,246
= −59.80
σ x (B) =
Mp qB
Ipp
−
Mq pB
Iqq
= +55.51

39. Normal
Stress
Calcula@ons:
Worked
Example
(2/3)
39
39
y
z
G
My
Iyy = 686,250 Ipp = 771,254
Izz = 436,250 Iqq = 351,246
Iyz = −168,750 αyp = 26.7°
yN = dn = 21.25
σ x (N) = β yN +γ zN
= 0.623×21.25+1.610× zN = 0
⇒ zN = −
13.24
1.610
= −8.22
N
tension
compression
point
of
max
tensile
stress
point
of
max
compressive
stress
Assume:
Calculate:
(which
gives
the
neutral
axis
GN)
elas0c
neutral
axis

40. Key
Learning
Points
(1/2)
1. The
simple
formula
of
bending
stress,
σx=Myz/Iyy,
is
valid
if
and
only
if
y
is
a
principal
axis
for
the
cross
sec@on
– That
is,
if
and
only
if
the
product
moment
of
iner@a
is
Iyz=0
– This
is
the
case,
for
instance,
when
y
and/or
z
are
axis
of
symmetry
2. To
calculate
Iyz
one
can
split
the
cross
sec@on
in
elementary
blocks,
sum
the
contribu@on
from
each
block
and
use
the
parallel
axis
theorem
– Important:
Iyz
can
be
nega@ve,
posi@ve
or
null
40

41. Key
Learning
Points
(2/2)
3. Knowing
Iyy,
Izz
and
Iyz
,
one
can
draw
the
Mohr’s
circle
for
the
second
moment
of
area,
which
allows
determining
the
extreme
values
(Imin
and
Imax)
and
their
direc@ons
4. In
the
general
case
of
unsymmetrical
bending,
the
normal
stress
is
given
by
the
formula
– σx=
βy
+
γz
• where
β
and
γ
depend
on
the
components
of
the
bending
moments
(My
and
Mz)
as
well
as
on
Iyy,
Izz
and
Iyz
5. The
above
formula
allows
determining
the
inclina@on
of
the
neutral
axis
41