dynamical analysis of soil and structures

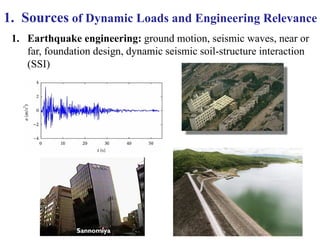
1. Earthquake engineering: ground motion, seismic waves, near or
far, foundation design, dynamic seismic soil-structure interaction
(SSI)
1. Sources of Dynamic Loads and Engineering Relevance
5

6
3. Blast and shock engineering: refinery design, homeland
security, defense industry, air and ground shocks, explosion,
mining, ...
2. Wind engineering: high-rises, long bridges, transmission
towers, tall chimneys

7
4. Dynamic foundation design or foundation isolation of
machines/equipment: pump stations, compressors and turbines, high-
tech buildings, wind turbines, …
5. Pile driving & capacity: impact and stress waves, hammer cushions,
bearing capacity determination, NDT, ‘wave equation’ method

6. Impact loading transmitted to foundation and
structures
8

9
7. Offshore foundation engineering
8. Geophysical methods & in-situ sounding

9. Dynamic design for high-speed transportations, tunnels,
buried pipelines
10
10. Construction induced vibrations
….

2. Theory of Dynamics & Vibrations
Basic principles:
• Newton’s laws in physics
• Free-body diagram for dynamic problems
2 types of systems:
• Discrete systems (finite number of degree of freedoms)
• Continuous systems (infinite d.o.f.s)
11
. ., 2 :
nd
e g law m
 
F a m

 i
f a

Discrete systems (finite number of degree of freedoms)
• Lumped mass system:
(a) Single or 1-dof system
12
x(t)
f(t)

(b) Multi-dof system (c) Continuum system
13

14
Analysis of a Single d.o.f. system (SDOF):
(a) sign convention
(b) Free-body diagram (FBD) for
x(t)
f(t)
m
k
c
(c) Write the equation implied by FBD:
( ): ( )
LHS RHS f t k x c x m x
     
   
( )
m x c x k x f t
  
  … a simple 2nd-order differential equation
cx

kx
=
m x

f(t)
m
i
F a



15
1st step: Free Vibration Problem:
Common canonical form of the ‘Equation of Motion’ by
dividing by m,
.... a 2nd-order homogeneous differential equation
0
m x c x k x
  
 
2
2 0 ................ (*)
n n
x x x
 
  
 
.......... ( / )
..........
2
2 2 2 ......
n
n
c n
k
where circular rad s
m
c
m
k
c m m km
m
natural frequency
fraction ofcritical damping / damping ratio
Critical damping constant






 
  
 
 
 

Solution of
Take
• Special case 1: =0 (i.e., undamped case)
16
2
2 0 ......... (*)
n n
x x x
 
  
 
2 2
(*) ( 2 ) 0
t
n n
A e
   
   
2 2
2
1,2
For non-trivial solution, must have ( 2 ) 0
.............. a simple quadratic equation whose 2 roots are
1
n n
n n
   
   
  
   
1,2 1 , , = 1
n n
i i
  
     
( )= ' '
n n
i t i t
x t a e b e
 

 
cos( t) sin( t
s )
cos in n
i t
n
i
n
e i
e i
 
 
 

  
 
Recall
   
( )= ' cos( t)+ sin ( t) ' cos( t)- sin ( t)
( ' ')cos( t) ( ' ')sin ( t)
= cos( t) sin ( t) !
n n n n
n n
n n
x t a i b i
a b i a b
a b
   
 
 

   

( ) t
x t A e


17
( ) cos( ) sin( ) (*)
sin( ) sin cos cos sin .
n n
x t a t b t
trigonometricidentity A A A
 
     
 
  
General solution
:
( ) ( ) 2
2 / ... "natural period"
1/ ... "natural frequency"
( / sec)
2 ... " natural frequency"
( / sec)
/ ....( / sec)
n n n
n n
n n
n n
n
t T t
T
f T
Hz cycle
f circular
rad
with k m rad
  
 
 

  
 
 

 

2 2
(*)... , sin cos , (*)
( )
where " " , " " .
To determine the 2 constants ( , ) or ( , ) in the general solution,
n
n
Taking t a A and b A then is equivalent to
x t A t
a
A a b
b
a b A
   
 


  
 
  
 
-1
= sin( + )
amplitude = phase angle = tan
use initia
0
0
:
(i) initialdisplacement x(0)= x
(II) initialvelocity x(0) = x
l conditions
 

Case (ii) >1 (over-damped case)
18
both are pure exponential decaying terms (no oscillation at all)
2
1,2 1,2
are both -ve from 1
n n
    
   
1 2
( )=
t t
x t a e be
 
 
 
Case (iii) =1 (Critically-damped case)
1 2
= ( . . )
n i e a double root
  
 
   
1
( )= +b +b n t
t
x t a t e a t e

 

 

19
   
2 2
2 2
1 1
1 1
( )= '
' '
n n n n
n n
n n
i t i t
i t i t
t t
x t a e e
a e e b e e
     
   
   
     
  
 

 
Case (iv) 0 <  < 1 (Under-damped case)
- most relevant to geotechnical & structural problems
2 2
1,2 1 1
n n n n
      
       
i
0
0
As in previous cases, can find the 2 constants :
1) initialdisplacement x(0)= x
2) initialvelocity x(0) = x
by initial conditions
 
 
 
 
2 2
1 1
2
= ' '
= ' '
sin ( )
1 ... " "
n n
n
n d d
n
i t i t
t
t i t i t
t
d
d n
e a e b e
e a e b e
e A t
where damped natural frequency
   
 
   
 
 
  
  

 



 
 

20
0 0
Imposing theinitial conditions of
(1) initialdisplacement x(0)= x , (2) initialvelocity x(0) = x ,
one finds
 

Applications: Determination of damping ratio by Logarithmic Decrement method
(for small )
21
1
1
from solution,
n N
n N
t
N
t
N
x Ae
x Ae
Note :
free vibration
zw
zw 






1
1
( )
1
n N
n N N
n N
t
t t
N
t
N
x e
Then e
x e
zw
zw
zw






 
 
 
 
nt
Ae zw


22
ᇱ
ே
ேାଵ
௡ ேାଵ ே ௡ ௗ
ௗ ௗ ௗ ௡
ଶ
ଶ

(II) Forced vibration
23
( )
m x c x k x F t
  
 
2
2 ( ) / ................ (*)
n n
or x x x F t m
 
  
 
0
0
Consider a common and basic form of dynamic load:
................ (*)
.... force magnitude
.... excitation frequency
( ) sin( )
F
F t F t




homog particular
( ) ( ) ( )
x t x t x t
 
General Solution to (*):
( ) ( ) forced vibration
free vibration
or x t x t
 

24
:
sin( ) cos( )
Take A t B t
P f
P
To find x (t) or x (t)
x (t)  
 
 
 
2 2 2 2
0
2 2
0
2 2
2 sin( ) ( 2 )cos( ) ( / )sin( )
/
2
0
2
n n n n
n n
n n
gives
A B A t B A B t F m t
A F m
B
          
   
   
       
 
      
 
     
      
 
2
P n P n P 0
Equation of motion x + 2ςω x +ω x = F / m sin(ωt)
 
2 2
cos( ) sin( )
sin( ) cos( )
then A t B t
then A t B t
P
P
x (t)
x (t)
   
   
 
  


   
 
   
 
2 2
0 2 2
2 2
2 2
2 2
2 2
0
.
/ 2
det / 2
0
/
det / 2
2 0
n
n n
n
n
n n
n
F m
A
F m
B
 
   
 
 
   
 

 
  
 
 
 
 
 
  
 

 
2x2 equations :Solution is (e g. by Cramer's rule)
[ ]
[ ]

25
   
 
     
 
   
 
     
 
2 2
0 2 2
2 2
2 2
2 2 2 2
0
2 2
2 2
2 2
0
2 2
2 2
0
2 .
/ 2
det / 2
0
/ ( ) / 2
/
det / 2
2 0
2 / / 2
n
n n
n
n n n
n
n n
n
n n n
F m
A
F m
F m
B
F m
x2 equations : Solution is (e g. by Cramer's rule)
 
   
 
     
 
   
 
     

 
  
 
 
 
    
 
 
  
 
 
   
 
   
 
   
2
0
2 2
2
0
2 2
2
/ (1 )
1 2
/ 2
1 2
n
F k
A
F k
B
with

 

 





 


 
 
  
 
  where
 
 
 
 

 
   
     
   
     
 
   
 
 
0 n
P 2
2 2
2
n
n n
ω
2ς
F / k ω
x (t) = sin(ωt - ) tan =
ω
ω ω 1 -
1 - + 2ς ω
ω ω
sin( ) cos( )
in A t B t
 
 
P
x (t)

26
 
 
1
( , )
w h ere
S
x



   
   
   
   
 
   
 
 
 
   
   
   
   
 
   
 
 
 

 
0
P 2 2
2
n n
0
2 2
2
n
n n
n
F / k
x (t) = sin (ω t - )
ω ω
1 - + 2 ς
ω ω
D y n a m ic A m p lifica tio n F a cto r Q u a si - S ta tic D eflectio n
ω
A .F . ς F / k
ω
ω ω
1 - + 2 ς
ω ω
ω
2 ς
ω
ta n
f
=
D e in itio n s :

 
 
 
2
n
ω
1 -
ω
: this means the forced response amplitude is
• ( , )
P S
n
Note
x x AF





Half-power method for 
using steady-state vibration test data
28
/
1
max
max
and
ark a horizontal line with and find its 2 intesection points
2
with the AF curve and their corresponding frequencies and
1. Identify peak/natural frequency peak amplitude
2. M
peak natural
A
A
w
w
Steps :
2
2 1
.
-
3. Then
2 2
peak peak
w
w w w
V
w w
D

;

36
A simple example of application:
Base isolation design for foundation
0
( ) sin( )
ground motion y t y t


( ) absolute displacement w.r.t. a fixed frame
x t 
Free-body diagram:
=
( )
k x y
 ( )
c x y

 
m x


37
FBDgives the equation: ( ) ( )
k x y c x y mx
    
  
0 0 )
Keeping unknown terms on LHS and prescribed term on RHS,
one gets ( ) sin( ) cos( ) .................(*
mx cx kx k y c y t y k t c y t
  
     
  
   
2 2
0 0 sin( ) ( )
ky c y t F t
  
   
0
Recall the forced response amplitude is
• ( , ), /
P S S
x x AF x F k
 
 
       
   
2 2 2 2
0 0 0 0
2 2
0
max 2 2
2
For (**), .
1 /
Thus
1- 2
p
n n
F ky c y y k c
y c k
x
 

 

 
   


   
   
    
   
 
   
 
 
2
2 2
2
0
1 2
1- 2
2
n
p
Max
n n
crit
x
y
noting c k m



 

 
 
 
  
 
 
 
 
   
   
    
   
 
   
 
 

Ground motion transmissibility

Ground motion transmissibility & design implications:
38

Dynamic Analysis by Complex Notation
39
Recall cos( ) sin( )
i t
e t i t

 
 
 
0 0
2
0
= (cos( ) sin( ))
or 2 .... (*)
/
i t
i t
n n
t i t
x x x
m x c x k x F e F
F m e


 
 

  
  
Consider
 
 
Take ( )=X ei t
x t 

Solution : 2
( )=i X e , ( )= X e !
i t i t
x t x t
 
 
   
 
   
 
0
2 2
0
0
2 2
2
(*)
(
)
( 2
) 2
( 2
)
1
/
n
n
n
n
n
n
t i
hen gives
m
whose solutio
i
X
n is X
i
k
F
F
m
F

   
 

 
   
 
 
 

 
 
 
 

 
   
 
 
   
 
  

 



Note:
1
its form is
a ib


40
0
2
2
2 2
2 2
2 2
:
1/
1 2
1 2
1
1 2 1 2
n n
n n
n n n n
Note
k
X
i
i
k
F
 

 
 

 
   
 
   

 
 
   
 
 
 
   
 
 
   
 
 
 
 
 
 
 
 
 
 
 
 
 
 
   
 
 
   
   
    
       
   
   
   
    
       
   
   
        
   
   
   
 
0
F




41
0 0
2
2
0 0
1
( ) ( ) ( )*
(1 ) 2
( ) is called the function.
Inversely,
(1 ) 2 ( ) (
n n
n n
k
X X F
i
where
k i X or
F or
F F
  
 

 

 
  
 
 
 
 
 
 
 
 
 
 
 
   
 
 
     
 
   
 
 
 
 
 
   
 
 
 
   
 
 
   
 
 
 
C
C Dynamic Compliance
K )
( ) is called the / function
for the model.
X
where  Dynamic Impedance Stiffness
K
i t
F e 
 ( ) i t
x t X e 
 
( )

C

42
0 0
0 0
:
( ) ( ) F sin(ωt) which is the of .
then the corresponding response x(t) must be the Imaginary part of X .
( ) ( ) F cos(ωt), which is the of .
then th
i t
i t
i t
a If F t F e
e
b If F t F e





Results
imaginary part
real part
e corresponding response x(t) must be the Real part of X i t
e 
0
= (cos(ωt)+isin(ωt))as to the equation of moti
a forced excitation of (cos(ωt)+i sin(ωt)), with
i.e., now we got the solution
F
i t
X X
e
0
2
2
0
2 2
2 2
2 2
/
1 2
1 2
1 2 1 2
( ) i t i t
n n
n n
n n n n
k
X e e
i
i
k
F
x t
F
 
 

 
 

 
   
 
   
 
 
 
   
 
 
 
   
 
 
   
 
 

 
 
  
 
 
  
 
 
    
 

   
   
    
       
   
   
   
   
       
   
   
       
   
   
   

(cos(ωt)+i sin(ωt))






 
 


43
2
0
2 2
2 2
2 2
,
1 2
( ) ( * ) sin( ) cos( )
1 2 1 2
i.e
n n
i t
n n n n
x t X e t t
k
F

 

 
 
   
 
   
 
 
 
 
 
 
 
 
 
 
 
 
   
  
 
   
   
   
       
 
   
   
   
   
       
 
   
   
       
   
   
 
   
 
0
For F(t) = sin(ωt)
Im
F
., exactly the same result we had before!

Method of Fundamental Solution (Duhamel integral)
for arbitrary forcing for SDOF
44

f()
t

f(t)
Concept: consider the loading as a sequence of many small impulses.
Tool needed: a Unit-impulse response function g(t,) which gives the
displacement of a dynamic system due to an impulse of unit magnitude at
time  with zero initial conditions.
1
0
We can then write
( ) ( , ) ( )
In the limit of & 0,
( ) ( , ) ( )
N
i
t
x t g t f
N
x t g t f d
  

  

  
   
 


f()
t

45
Next, need g(t,):
: ( ) ( )
.
0 for t except 0
, ( ) 0
( ) 1
.
Solution m x c x k x t or m g c g k g t
with zero initial conditions
at t
In the above the function t at t
t dt
is called the
   




       
 
 
 
 
 
  
 
 
 

 
 

deltafunction
   
t
1/


46
(1) 0 ,
For t 
  0
m g c g k g
  
 
with zero initial conditions
(2) , 0... !
For t m g c g k g free vibration problem also

   
 
( , ) 0
g t 
 
.
o let's use the general free-vibration solution of
( , ) sin( ) .
nt
d
But likely non zero conditions at t after the impulse at time
S
g t A e t for t

 
   


 
  

47
 
+
+
(3) Theimpulse effect going from t= to :
: Consider ( )
Idea m g c g k g t dt


 
 


   
  
+
+
+ +
+
:
1st term: ( , )
2nd term ( , ) 0
3rd term ( ) 0
LHS
m g dt m g m g
m g dt m g m g
m g dt m g dt m g
 


 


 
 
 
 
 






 



 
  
   


 
  

+
:
( ) 1
RHS
t dt


 

 


48
LHS:
1
( , ) 1 ( , )
( , ) 0
m g or g
m
g
   
 
 


 

 
( )
:
0
( , ) 1
sin( ( )
n t
d
d
Summary
for t
g t
e t for t
m
 


  

 

 
 
  
 
 
 
( )
0
giving the solution under arbitrary forcing as
1
( ) sin( ( ) ( )
.
n
t
t
d
d
x t e t f d
m
the
 
   

 
  

Duhamel Integral
1
0
d
A
m

 


Practical Numerical Evaluation of
49
( )
0
1
( ) sin( ( ) ( ) for arbitrary ( )
n
t
t
d
d
x t e t f d f t
m
 
   

 
  

( )
0 0
( ) sin( ( ) sin( )cos( ) cos( )sin( )
( )
sin( ) cos( )
( ) cos( ) ( ) sin( ) ( )
n n n
n n
n n
d d d d d
t t
t t
t t
d d
d d
d d
Note
i t t t
ii e e e
e t e t
x t e f d e f d
m m
    
 
   
       
 
       
 
   
 
 
  

   
 
The two integrals can be numerically by trapezoidal rule or Simpson rule for arbitrary ( ).
f t
Remarks:
1. Good for arbitrary loading
2. Dumhamel integral (a convolution integral)
3. A time-domain method (vs frequency-domain methods)

Numerical Step-by-Step Time Integration Methods
 Direct time-domain procedures
 Allow for nonlinear problems (e.g., a change in k, c, or m as a function
of time and deformation)
 Arbitrary loading time function
 Variety of algorithms and propoals
 Commonly used in FEM, FDM, BEM
 Underlying numerical and discretization issues
50
x(t)
f(t)
m
k
c
f(t)
t
t

51
Idea:
f(t)
t
t
x(t)
t
t
t
x
x
x
 
 
 
 
 

 t+ t
x
x
x 
 
 
 
 
 


forcing
t+2 t
x
x
x 
 
 
 
 
 


forcing
( ) .
m x c x k x f t with some prescribed initial conditions
  
 
t t+t

52
Assumption: the acceleration varies linearly in the time interval of t.

Example : Linear acceleration method :
Writing ( ) , ( ) , ( ) ,
the assumption ( ) 0
t t t
t t t
t
x t x x t x x t x
x x
x t x for t
t
  

  

 
      
 

 
   
 
 
0
2
( ) ( )
2
t
t t t
t t
x t x x t d
x x
x x
t

  

 
 
    
 

    

 

  
 
 
0
2 3
( ) ( )
2 6
0 .
t
t t t
t t t
x t x x t d
x x
x x x
t
for t

  
 



 
   
 

     

 
  
 
 
 

t
x

t t
x 

t t
 
t

53
Taking = t, eq (1),(2), (3) become
 
( ) (1)
t t
x x t t
   
 
( ) (2)
2 2 2
t t t t t t t t t t t
t t t
x x x t x x x x x
  
  
       
       
2 2
(3)
3 6
t t t t t t
t t
x x x t x x

 
 
    
  
i.e., the primary unknown is t t
x 

To find it,
( ) ( ) !
t t t t t t t t
m x c x k x f t at t t m x c x k x f t
   
        
   

54
( )
t t t t t t t t
m x f t c x k x
   
  
 
2 2
( ) ( ) ( )
2 2 3 6
t t t t t t t t t t t
t t t t
f t c x x x k x x t x x
  
   
        
     
2 2
,
[ ] ( ) ( ) ( )
2 6 2 3
t t t t t t t t t
Collecting the terms
t t t t
m c k x f t c x x k x x t x
 
   
        
    
2 2
1
leading to
[ ] ( ) ( ) ( ) (*)
2 6 2 3
t t t t t t t t t
t t t t
x m c k f t c x x k x x t x

 
 
   
        
 
 
    


55
      
1 1
With and computable bymeans of (2) and (3) upon obtaining , one can
collectivelydetermine the displacement, velocityand acceleration at according to
w
[ ] [ ]
t t t t
t t t t t t
t
x x x
t t
 
  
 

 
x f B x
A A
 
   
here
upon defining .
[ ], t t
t
t
x
x
x
and 
 
 
 
 
 
x
B f
A


2
This is a step-by-step algorithm by which
.... !
t t t t t t n t
x x x x
x x x x
x x x x
    
       
       
  
       
       
       
   
   

56
Note:
1) Concept of stability, accuracy, efficiency
a) Conditionally and unconditionally algorithms: a critical time step tcrit
if conditionally stable.
b) Accuracy: Level of numerical amplitude decay/damping & phase shifts
due to accumulation of errors.
c) Explicit and Implicit schemes.
d) Short duration versus long-duration problems.
e) Applicable to MDOF systems (see posted reading)
a) Other methods e.g., Central difference, Newmark method in many
commercial FEM codes (see posted reading)

5
Response Spectrum (a spectral method)
The maximum response of a Single degree of freedom system with
general to a specific excitation (e.g., earthquake ground
motion) :
( , )
n
 
 
2
2 ( )
g
n n g
c x k x m x x
or
x x x x t
 
   
   
  
  
=
-kx-cx m (x+ x )
g
  
( )
g
x t

/
g
x g


6
( )
0
( )
2 0
Analytically, thedisplacement response is expressible in the Duhamel integralform as
1
( ) sin( ( ) ( )
1
sin( ( ) ( ) ..... (*)
1
n
n
t
t
d
d
t
t
d g
n
x t e t f d
m
e t x d
 
 
   

   
 
 
 
  
   


 
max v
pv
( ) ( , ) ....
( , ) ....
d
d
x t S
S
 
 
 Spectral velocity
Spectralpsuedo velocity


 
( )
0
1
( ) ( ) sin( ( ) ( )
n
t
t
d g
d
d
b x t e t x d
dt
 
   

 
   

 
 
( )
pv max
0
( , ) sin( ( ) ( ) is
n
t
t
n d g
S e t x d called
 
     
 
  
 SpectralPsuedo- Velocity

Leibniz rule :
 
0 0
0
( , )
( , ) ( ) ( , ) ( ) ( )
( , )
( )
t t
g g g
t
g
d dt g t
g t x d g t t x t x d
dt dt t
g t
x d
t

    

 

  




 

  

  a
max
(c)
( ) ( ) ( , ) ...
g d
x t x t S  
  Spectralacceleration
 
max
pv
( ) ( ) ( , ) ....
1
( , )
d d
n
n
a x t S
S where
 
 


Maximum response quantities :
Spectral Displacement


7
   
: eqn of motion g
gives m x x c x k x
   
Note   
   max
max
1
g
implies x x c x k x
m
   
  
  2
max
g n d n
k
x x S
m
 
    
d pv
S S
 
Summary of Approximate relations of
Spectral displacement, velocity and acceleration to
Spectral pseudo-velocity
d pv
n
V pv
a n pv
1
S = S
ω
S = S
S = ω S
2
n
n
with
T

 

8
2
2
n
n
T
T




d pv pv
n
V pv
a n pv pv
1
S = S S
ω
S = S
S = ω S S
log log log log(2 )
log log log log(2 )
n
n
T
T


   
   
d pv
a pv
S S
S S
y = m x +b
Line of constant Sd
Line of constant Sa

9
Tripartile plot of response spectrum

11
Frequency domain analysis
0 0 0
1 0 0
Recall for periodic functions of period T:
2 2
f(t)= sin( ) cos( ), ( )
n n
n n
a n t b n t or T
T
 
  

 
 
  
 
Fourier series
0
0
0
0
0
0
0
0
where
f(t) sin( )
f(t) cos( )
n
n
a n t dt
b n t dt




















0
0 0
0
/
0
/
A much more compact form is
f(t)= = f(t)
2
in t in t
n n
n
F e with F e dt
 
 
 






 
 
0
0 0
0
/
0
/
or
f(t)= = f(t)
2
in t in t
n n
n
F e with F e dt
 
 
 






 
 
t
f(t)

12
0

0
2
0
 0
3
2 2
n n
a b

Can determine the phase angle of magnitude of
each sinusoidal component of f(t)
ie f(t) can be looked upon as a sum of sin( ) !
n n n
A n t
 

Can determine the amplitude/magnitude of each
sinusoidal component of f(t) as 2 2
n n
a b


13
( )= f(t) i t
F e dt







(e.g. an earthquake ground motion or response)
Next : How to treating as non -perioidc function?
0 0 0 0
2
( ) , ( ) / , ( ) , ( ) ( )
n
a d b c n d F F
T

      
      
 
1
f(t)= ( )
2
i t
F e d

 



 
0
1 1
then (*) becomes f(t) ( ) (2)
2 2
in t i t
n
n
F e d F e d
 
  
 
 



 
 

The Fourier transform of f(t) Inverse Fourier transform of ( )
F 

0
0 0
0
/
0 /
Note that
1
f(t)= = f(t) (*)
2
in t in t
n n
n
F e with F e dt
 
 
 






 
 
In the limit of T  
leading to

15
Remarks:
 is generally a complex-valued function of
frequency, i.e., with a real and an imaginary part.
 is the Fourier amplitude spectrum (real value)
 Exposes the frequency content of the loading or
response
 It is a full characterization of f(t) in the frequency
domin
 i.e.,
 FFT algorithms (Fast Fourier Tranform)
( ) gives ( ) and ( ) gives back ( ) !
f t F F f t completely
 
 
( )
F 

( )
F 


13
( )= f(t) i t
F e dt







(e.g. an earthquake ground motion or response)
Next : How to treating as non -perioidc function?
0 0 0 0
2
( ) , ( ) / , ( ) , ( ) ( )
n
a d b c n d F F
T

      
      
 
1
f(t)= ( )
2
i t
F e d

 



 
0
1 1
then (*) becomes f(t) ( ) (2)
2 2
in t i t
n
n
F e d F e d
 
  
 
 



 
 

The Fourier transform of f(t) Inverse Fourier transform of ( )
F 

0
0 0
0
/
0 /
Note that
1
f(t)= = f(t) (*)
2
in t in t
n n
n
F e with F e dt
 
 
 






 
 
In the limit of T  
leading to
A Fourier transform pair

15
Remarks:
 is generally a complex-valued function of
frequency, i.e., with both real and imaginary parts.
 is the Fourier amplitude spectrum (real value)
 Exposes the frequency content of the loading or
response
 It is a full characterization of f(t) in the frequency
domin
 i.e.,
 FFT algorithms (Fast Fourier Tranform)
( ) gives ( ) and ( ) gives back ( ) !
f t F F f t completely
 
 
( )
F 

( )
F 


16
Basic operational properties:
Fourier transformof derivatives:
[ ( )] ( ) ( )= ( ) w
w
¥
-
-¥
Á = = ò
  i t
recall f t f t F f t e dt
( )
( )
2
( ) [ ( )]= ( ).
[ ( )]
( )
w
w
w w
¥
-
-¥
Á
= Á
=
ò
 


i t
d
b f t f t e dt
dt
i f t
i F
F
( )
( )
( ) [ ( )]= ( )!
w w
Á 
n
n
c f t i F
( )
In integration by part, ( ) ( )
( ) ( )
( ) ( ) 0@
w
w
w w
w
w w
-
¥
-
-¥
¥
¥
- -
-¥ -¥
= -
= +
=  ¥
ò
ò

i t
i t
i t i t
de
f t e f t dt
dt
f t e i f t e dt
i F if f t
( )
) [ ( )]= ( ) ( )= ( ) w w
w
¥ ¥
- -
-¥ -¥
Á = =
ò ò

  
 i t i t
df t
a Consider f t f t F f t e dt e dt
dt

17
:
( )
Solution of SDOF equation of motion under arbitrary forcing
m x c x k x f t
  
Applications :
 
 
To apply Fourier tranform method, consider
( ) i t
m x c x k x f t e dt

  
 
2
( ) ( )
( )
m i c k X F
 
 
 
    
 
 
2
( ) ( ) ( ) ( )
( )
( ) ( )
( ) ( ) .
i t
with
i m X i c X k X F
X x t e dt as the Fourier tranform of x t etc

   

 



   

   

 
( ) i t
m x c x k x f t e dt



  
  

18
2
( ) ( )
1
X F
m i c k
 
 

 
  
  
 
 
or
2
2 ( ) / ................ (*)
n n
x x x f t m
 
  
 
 
2 2
( ) ( )
(*) ( ) 2 /
n n
then gives i X F m
 
   
   
 
 
2 2
2
( )
( )
( )
( ) 2
1
(1 ) 2
n n
n n
m
X
i
k
i
F
F



   
 

 
 
 
 
 
 
 
 
 
 
 
 
  
 
 
   
 
 
     
 
   
 
 
 




19
2
: :
. : 2 ( )
n n g
Example Earthquake ground motion problem
Eq of motion x x x x t
 
   
  
 
 
2 2
/
( ) ( )
( ) ( )
1
( ) 2
n n
x x
X x
i
x
 
 
   
 
 
  
 
 
 
 H 
 



Concept of a Transfer function
Excitation Response
Transfer function
H()

19
2
: Earthquake ground motion problem:
. : 2 ( )
n n g
Recall Eq of motion x x x x t
Example
-
 
  
  
 
 
2 2
/
( ) ( )
( ) ( )
1
( ) 2
g
n n
x x g
X x
i
x
H
 
 
   
 
 
  
 
 
 
 
 



Concept of a Transfer function
Excitation Response
Transfer function
H() of dynamical
system

20

( )
g
x w



( )
X w


( )
w
H

21
Remarks:
 Theoretical modeling characterization of dynamic and
vibratory systems in frequency domain
 Other transfer functions of engineering
interest
/ v/ /
( ), ( ), ( )
. ., g g g
d a a a a
e g H H H
  
 Experimental determination of transfer functions
of physical systems

22

( )
w
H
In more complex systems:

23
2
: (2 )
g n n
a x x x x
Note  
    
  
2
(2 )
n n
a x x
 
   

  
:
: !
g g
g
a x x a x x
Note a x x
Note     
 
 
    
 
  
 
2 2
( ) )
1
( ( )
( ) 2
n n
With X
i
x
 
   
 
 
 
 
 
 
 

 
2
2 2
( )
1
( ) 2
n n
a x
i


   
 

 
   
 
 
 

 
 
 
2
2 2
( )
2
( ) 2
n n
n n
i
a x
i

  
   
 
 

 

 
 
 

 
Re
Im
Z1+ Z2
Z2
Z1

Method of Energy Balance
29
 
2 2
1 1
( )
2 2
Kinetic energy m x Potential elastic Energy k x
For a 1DOF :
 
&
x(t)
f(t) A
B
0
( ) sin( ) ( ) sin (
F t F t x t A t for
+ ) undamped free vibration
  
  
 
 
2
2
2
2
Note that KE+PE=
At time A, KE+PE=0 ,
1
2
1
At time B, KE+PE=
2
0
2
1 1
2
n
n n
k A
m A
k
k A m A
m
Conservation of energy
w
w w


 


constant for undamped case

Method of Energy Balance
30
2 / 2 / 2 /
0
Idea: Compare Input nergy & energy dissipated per cycle
( ) sin( ), ( ) sin( ), ( ) cos( )
( ) ( ) sin( )
T T T
input o o o
E
F t F t x t A t x t A t
dx
W F t dx F t dt F t A
dt
p w p w p w
w w f w w f
w w
D
  

    
   
  
Damped 1DOF under Forced Steady State Vibration :
&
 
2 /
0
2 /
2
0 0
cos( )
sin( ) cos( )cos( ) sin( )sin( ))
sin( ) sin ( ) sin( )
T
o
T
o
t dt
F A t t t dt
F A t dt F A
p w
p w
w f
w w w f w f
f w p f



  
 


x(t
) f(t)
 
2 / 2 /
2
2 /
2
( ) ( )
cos( ))
.....
T T
dissip damping
o o
T
o
dx dx
W F t dx t c dt
dt dt
c A t dt
cA
p w p w
p w
w w f
wp
D
 

 
  
 
 
 


 


31
0
2
0
os( )
sin( )
................ (*)
: input dissip
input
dissip
W W
W F Ac
For steady state must ha
W c A
F
A
c
ve
p f
pw
f
w
D D
D
D



 
0
2
max 2
2
/
C a (*) is ident
: ical t
-
o
l
2
im
1
p
n n
F k
x
w w
V
w w

   
   
    
   
 
   
 
 




Hysteretic cyclic stress-strain behavior
in many real materials
32
Area  energy dissipation



Linear viscous model vs physical cyclic stress-
strain behavior :
33
Hysteretic loop’s area’s strong frequency dependency in
linear viscous damper not seen in real materials
x
F

Equivalent Viscous Damping
34
exp
2
exp
2
( ' )
................ (*)
erim
dissip
erim
W c A W hyster loop s area
W
and define
ak
A
T e
equiv
Idea
c
:
pw
pw
D D
D
 

2 2
exp
2
2
(2 )
(2 )
2
equiv equiv
erim crit
crit crit
equiv n
n
equiv
n
c c
W
c
Ta A c A km
c
A km
A
ke
k
Minor - arrangement :
pw pw
w
z p w
w
w
p z
w
D  

 
  
 
exp
2
!
1
4
2
erim
equiv
n
W
kA
z
w
p
w
D
 
   
   
 
 
2
exp
1
4
2
erim equiv
n
W kA
w
pz
w
D
   
    
 
 

• If experimental measurement is done at
35
exp exp
2
!
1 4
4
2
erim erim
equiv
W W
Triangular Area
kA
z
p
p
D D
 
 
 
 
n
 



A

Shear Modulus and Damping:
Stress‐strain response is hysteretic and strain level dependent
Basic engineering parameters:
‐secant modulus G
‐equivalent viscous damping 
both of which are dependent on level of confinement/stress state
2
1
4
2
loop
equiv
G
Area
G



 


 
 
 

• Soil is a particulate/porous
medium
• Under a water table, void
space in the ‘soil skeleton, is
filled by water with pore
water pressure u
SOLID GRAINS
WATER

Importance of effective stresses:
They control:
(a) Shear strength/failure condition in soil
(b) Stiffness/deformability/settlement of foundations
v v
vertical soil effective stress
horizontal soil effective stress h h
u
u
 
 
  
  
v
h



Concept of Effective Stress in Soil
u

In 3D:
Note: Sign convention in soil mechanics:
Compressive stress is positive

Field Measurement Methods:
(I) For low  level (<10‐6 to 10‐4 ) ….. Gmax
(II) Geophysical/wave‐based methods (downhole, cross hole seismic
measurements)
(III) Impulse or low‐level vibration methods
(IV) Shear wave speed: Compressional P‐wave speed:
2 1
1 2
p
G
V

 

 
  

 
s
G
V



Typical range of Vs:
200’/s to 1500’/s for unconsolidated soil.
2000’/s for stiff soils
3000’/s for sandstone
>6000’/s for rocks
E.g., =100 lb/s, Vs=300/s:
Gmax =(100/32.2)(300)^2 = 0.28x106 lb/sqft(psf)
Gmax =(100/32.2)(1500)^2 = 7x106 lb/sqft(psf)
1psf=47.85Pa
1 psi=6.891 kPa

DIFFERENT LABORATORY TESTS FOR DIFFERENT STRAIN LEVELS

Laboratory methods:
Resonant column tests:
‐excited torsionally (or axially) at the top or base
into resonant modes
‐transducers used to measure motion’s time
histories
‐sinusoidal or random excitation
‐use of solid or hollow samples
‐ Equiv viscous damping ratio from hysteretic loop
(r)

Lab tests for higher strain level:
(a) Cyclic simple shear test
Can be stress‐control or strain‐controlled
Drained or undrained (pore pressure development)
Simple shear (stack rings) vs direct shear test
cyclic
h0

cyclic

v0
(v0 ,‐cyclic)
(h0 ,cyclic)

(b) Cyclic triaxial test:
Repetitive axial compression/extension ‐ different stress path
stress control or strain controlled
Drained or undrained (pore pressure development)
0

0+d‐cyclic

d‐cyclic
(0 ,0)
, ,
2(1 )
E
E G G
   

  

~ 0.15 to 0.35 (sand)
0.5 (saturated clay)



(c) Bender element test
Piezoelectric sensors (transmitter and receiver)
Measure average wave speed between 2 points in specimens
s measured
L G
V
t 

 

+ ‐

(d) Shake Table Test
others….

Experimental Synthesis and empirical relationships:
 Gives trends with respect to basic factors
 Different functional forms proposed
 Useful for preliminary assessments

Primary factors affecting shear modulus & damping ratio
Strain amplitude
Mean effective stress
Void ratio
Relative density Dr (sand)
Secondary factors
# of cycles, OCR,  & c, grain characteristics, soil fabric &
structure, frequency, degree of saturation, cementation

Empirical relationships on shear modulus:
 Useful for preliminary assessments
 Gives trends with respect to basic factors
 
 
1/2
2
max 1/2
2
. ., (1972)
(2.973 )
1230 ... angular grains
1 1
( ) ( ~ )
(2.17 )
2630 ... round grains
1 1
0 0
20 .18
40 .30
60 .41
k mean
k mean
e g
e
OCR
e psi
G psi
e
OCR
e psi
PI k
where
-4
Hardin & Drnevich
10



 

 

 
 

 
 
  

 
 

 
 
  
 







 
 
 
 


units of G and p = kg/cm2
Iwasaki et al. (1978)

1/ 2
2
4
2
0..44
2
2 5
max 2
0..4
2
6
2
(1978)
(2.17 )
700 , @10
1 1 /
(2.17 )
( / ) 850 , @10
1 1 /
(2.17 )
900 , @10
1 1 /
mean
mean
mean
e
e kg cm
e
G kg cm for sand
e kg cm
e
e kg cm









 

 

 
 

 
 
 

 

 
  
 
  
 
 

 

 
 
 
  
 
Iwasaki et al

Seed and Idriss (1970)
Separate sand and clay
     
 
1/ 2
max 2 2
max max
2
max
( ) 1000 , 15 0.6 ,
1
0.6 , 2 ,....
( / ) ( , )
mean
u
G psf K K Dr F
psf
F for silt F for gravel
G
kg cm f OCR PI
S
Sand :
Clay :
 
 
  
 
 
 

𝐾

Strain dependence of cyclic shear modulus
• Basic observations: (a) γ
τ
γ
m
m c
g
g
t
= +
max
( ) ,
i As g t t
 ¥ 
m c
g
t
g
 =
+
max
1
m
t
 =

max
0
( ) 0,
d
i As G
d g
t
g
g =
 
( )
2
1
d m
d m c m c
t g
g g g
æ ö
æ ö ÷
ç
÷
ç ÷
ç
÷
 = - ÷
ç ç
÷ ÷
ç ÷
ç ç
+ ÷
è ø ç +
è ø
max
0
1
d
G
d c
g
t
g =
 = =
1 1
1
( ) ( )
max max
max max max
G G
G G G
g
g
g t g t
= +  = +
Summary :
( ) 1 1
1
1
max
ref
max
max max
ref
max
G
where
G
G G
t
g
g
g g
g
t
 = = =
+
+



(v ,ult)
(K0v ,‐ult)
cyclic
 c’
max/ult
v
K0v


Basic observation: (b)
1
(i) reverse slope Gmax
(ii) half area of loop constant% * triangle a_b_c’s area
triangle abc’s area
k
»
»
= 
max
1
triangle abc’s area= (ad)(cd-cb)
2
where ad =2
2 /
2 /
cd G
bd G
t
t
t
⋅
=
=
2
1 1
max max
1 1 1 1
area of hyeteretic loop= (2 )2 = 4
k k
G G G G
t t t
æ ö æ ö
÷ ÷
ç ç
÷ ÷
⋅ - -
ç ç
÷ ÷
ç ç
÷ ÷
ç ç
è ø è ø
2
1
1
max
2
max
max
max
1 1
4
2 ( )
= 1
1
4 (
2
( )
1
k
k
G G G
Equivalent damping ratio
G
G
G
G
t
g
t p
p
g
z z
æ ö
÷
ç ÷
-
ç ÷
ç æ ö
÷
ç
è ø ÷
ç ÷
= -
ç ÷
ç ÷
ç
è ø
æ ö
÷
ç ÷
 = -
ç ÷
ç ÷
ç
è ø

g
1
( )
0
max
G
G
g
1
0
( )
max
z g
z

Concept of Strain‐compatible shear modulus and damping
To recognize the significant strain‐dependence of the shear modulus and damping ratio,
one generally needs to use a pair of G and  in the dynamic analysis of the model so that
their values are consistent with the strain/deformation level of the response.
Approach:
1. Assume an initial estimate of strain, say, 0 & obtain G(0)
and  (0).
2. Perform dynamic analysis to find the predicted strain level,
say, 1.
3. Check if 1 ‐ 0 is close enough.
4. If not, replace 0 by 1 and repeat step 1 to 4
until difference of the different n+1 and n is
acceptable
5. Then G( n+1) and  (n+1) are called the
Strain‐compatible shear modulus and damping ratio.
* The iterative approach is built in the program SHAKE 91,
2000 for 1‐D equivalent linear ground response analysis
1
( )
0
max
G
G
g
1
0
( )
max
z g
z
0

Multi‐Degree of Freedom Systems
 Soil layering and profile variation
 Improve accuracy and lower degree of
approximation
 Higher‐order wave motion at high
frequencies

Multi-D-O-F system  Continuum system
2

m1
f1(t)
x2(t)
f2(t)
H/2
H/2
, G
, 2G
FBD for Equations of motion for undamped case:
x1(t)
k1
k2
1 1
m x

f1 = 1 1 1 1 2 1
( )
m x k x f
x
 + - =

1 1 2
( )
k x x
-
2 2 1 1 2 2 2 2
2 2 1 1 1 2 2 2
( )
( )
m x k x x k x
or m x k x k x
f
f
k
 + =
+
- -
- + =


f2
2 2
k x 2 2
m x

=

FBD for Equations of motion for undamped case:
1 1 1 1 2 1 (1)
( )
m x k f
x x
+ - =

2 2 1 1 1 2 2 2
( ) (2)
m x k x k k x f
- =
+
+

{ } { } { }
In matrix form  [M] x + f
=
[K] x

{ } { }
1 1
2 2
For the 2-DOF model of the soil layer,
0
....
0
....
3
, ....
m
Mass matrix
m
k k
Stiffness matrix
k k
x f
forcing vector
x f
é ù
ê ú
=
ê ú
ë û
é ù
-
ê ú
=
ê ú
-
ë û
ì ü ì ü
ï ï ï ï
ï ï ï ï
= =
í ý í ý
ï ï ï ï
ï ï ï ï
î þ î þ
[M]
[K]
x f
Note:
M and K are symmetric

{ } { } { } { }
For a damped system, the equation of motion is
+
[M] x [C] x +[K] x f
=
 
{ } { } { }
Case 1: Free vibration of undamped MDOF:
+
[M] x [ 0
=
K] x

{ } { }
{ } { }
) (0)
) (0)
subject to
a
b
=
=
Initial Conditions :
x x
x x
 
Note: Same matrix equation of motion from finite element
methods

{ } { } { } { }
For a damped system, the equation of motion is
+
[M] x [C] x +[K] x f
=
 
{ } { } { }
Case 1: Free vibration of undamped MDOF:
+
[M] x [ 0
=
K] x

{ } { }
{ } { }
) (0)
) (0)
subject to
a
b
=
=
Initial Conditions :
x x
x x
 
Note: Same matrix equation of motion from finite element
methods
{ } { }
As in SDOF:
!
i t
e w
I
=
dea :
x η

{ } { } { } [ ]{ } { }
[ ]
{ }
[ ]
2
2
where the matrix
For non-trivial solution of , must have
det 0.
or
one
w
w
 - + =
é ù
= - +
ê ú
ë û
=
)
=
[M] η [K] η 0 H(ω η 0
H(ω) [M] [K]
η
H(ω)
[ ]
[ ]
2
2
2
2 2 2
0
For the 2-dof example,
0 3 3
with the determinant det ( )( 3 )
m k k m k k
m k k k m k
m k m k k
w
w
w
w w
é ù
é ù é ù
- - + -
ê ú
ê ú ê ú
=- + =
ê ú
ê ú ê ú
- - - +
ë û ë û ë û
= - + - + -
H(ω)
H(ω)

[ ]
( )
( )
2
4 2 2
2
1
2
2
Settingdet 0 4 2 0, a quadratic equation in .
: (2 2) 0.585
(2 2) 3.414
Theyare the of t
k k
m m
k k
Roots
m m
k k
m m
w w w
w
w
æ ö æ ö
÷ ÷
ç ç
=  - + =
÷ ÷
ç ç
÷ ÷
ç ç
è ø è ø
æ ö æ ö
÷ ÷
ç ç
= - =
÷ ÷
ç ç
÷ ÷
ç ç
è ø è ø
æ ö æ ö
÷ ÷
ç ç
= + =
÷ ÷
ç ç
÷ ÷
ç ç
è ø è ø
H(ω)
naturalfrequencies
1
he MDOFsystem.
Put in ascending order, the lowest frequency, i.e., is called the Fundamental natural frequency.
w

Modal shapes associated with each natural frequency
{ } { } { }
( )
( )
{ } ( )
2 1
1 1
1
2
: ... (*) will allow non-unique solutions
2 , (*)
1 2 1 1 2
0
normalize it in
0
1 1 2 1
For a
For the dof system can be reduced to
or
w w
h
h
é ù
- +
ê ú
ë û
é ù ì ü
- + - ï ï
ì ü ì ü +
ê úï ï ï ï ï ï
ï ï ï ï ï ï
ê ú =  =
í ý í ý í ý
ï ï ï ï ï ï
ê ú ï ï
- + î þ
ï ï ï ï
î þ ï ï
ê ú î þ
ë û
1
1
1
[M] [K] η = 0 η
η
{ } { } { }
( )
( )
{ } ( )
2 2
2 2
1
2
different ways
: will allow non-unique solution
1 2 1 1 2
0
0
1 1 2 1
For a
w w
h
h
é ù
- +
ê ú
ë û
é ù ì ü
- + - ï ï
ì ü ì ü -
ê úï ï ï ï ï ï
ï ï ï ï ï ï
ê ú
 =  =
í ý í ý í ý
ï ï ï ï ï ï
ê ú ï ï
- + î þ
ï ï ï ï
î þ ï ï
ê ú î þ
ë û
1
2
1
[M] [K] =
η 0 η
η

{ } { } { }
{ } { } { }
{ } { } { } { } { } { }
{ } { } { } { } { } { }
2
2
2
2
..... (1)
..... (2)
0 ..... (1)
..... (2)
But since the matirx
i i
i
j j
j
T T T
j i j i j
i
T T T
i j i j i
j
and
is also true
w
w
w
w
- + =
- + =
- + = =
- + =
Orthogonality of Mode Shapes
Note : [M] η [K] η 0
[M] η [K] η 0
Observation :
η [M] η η [K] η η 0
η [M] η η [K] η η 0
[K]
{ } { } { } { } { } { }
( ){ } { }
{ } { }
{ } { }
2 2
!
( , too) is symmetic, it is always true that
.
,
(1) (2)
0
0
, !
0
T
j i
i j
T
j
j i
i j
T i
j i
f
and
Ta
i
k
f
i g
i
n w w
w w
w w
-  =
= ¹
=
-
 ¹

T T
T T
[M]
a [K] b = b [K] a a [M] b = b [M]
η
η [M] η
η [K]
a
[M] η
η
{ } { }
We say that the mode shape
with respect the the mass matrix and the stiffness matrix .
i j
is orthogon
]
al
η η
[M
t
[K]
o

Usefulness:
If we put the mode shape vectors in a matrix form
{ } { } { }
{ } { }
{ } { }
1 2
... N
T
T
i i
ii
T
T
i i
ii
then must be
with the diagonal element
must be
with the diagonal element
é ù
= ê ú
ë û
 =
L =
=
Q =
[T] η η η
[T] [K][T] [Λ] a diagonal matrix
η [K] η
[T] [M][T] [Θ] a diagonal matrix
η [M] η
. . diagonalizes both the !
i e and matrices
[T] [K] [M]

0
&
0 3
1 2 1
1 2 1 2
,
1 1 1 2 1
m k k
m k k
é ù é ù
-
ê ú ê ú
= =
ê ú ê ú
-
ë û ë û
é ù
é ù +
+ - ê ú
ê ú
= = ê ú
ê ú
-
ê ú
ë û ë û
T
E.g. For the 2- DOF example of the 2- layered soil,
[M] [K]
[T] [T]
( )
( )
1 2 1 1 0 1 2 1 2
0 1 1 1
1 2 1
T
m
é ù
é ù ê ú
é ù
é ù
+ + -
ê ú ê ú
ê ú
ê ú
= = =
ê ú ê ú
ê ú
ê ú
-
ê ú ë û ê ú
ë û
ë û ê ú
ë û
2
2
1+ 2 +1 0
[T] [M][T] m [Θ]
0 1- 2 +1
1 2 1 1 1 1 2 1 2
[ [ ]
1 3 1 1
1 2 1
T
k
é ù é ù
é ù é ù
+ - + -
ê ú ê ú
ê ú ê ú
= = =
ê ú ê ú
ê ú ê ú
-
-
ê ú ë û ë û
ë û
ë û
4 0
T] [K][T] k Λ
0 4

Modal Analysis of MDOF:
Observation and Ideas:
(i) If the mode shapes are orthogonal to each other. If so, they must be
independent of each other!
(ii) That means any x can be decomposed into a linear combination of
the mode shapes , 1, 2 ...,
i
i N
=
η
{ } { } { } { }
{ }
1 2
1 2
1
2
1
. . ( ) ( ) ( ) ... ( )
( )
..
N
N
N
i
i
i
N
i e t q t q t q t
q
q
q t
q
=
= + + +
ì ü
ï ï
ï ï
ï ï
ï ï
ï ï
ï ï
é ù
= = í ý
ê ú
ë ûï ï
ï ï
ï ï
ï ï
ï ï
ï ï
î þ
å 1 2 N
x η η η
η η η ... η
{ } { }
( ) ( )
t t
=
i.e. let'swrite x [T] q
The s are called the 'Principal' or 'Normal' coordinates of the dynamical system
i
q

With , the equation of motion
{ } { }
( ) ( )
t t
=
x [T] q
{ } { } { } for free vibration of undamped MDOF becomes
+
[M] x [K] x = 0

( )
t
 +
[M][T]q [K] =
[T]q 0

( ) ... (*)
t +
T T
[T] [M][T]q [T] [K] =
[T]q 0

( )
( ) ( )
( )
( )
( ) ( )
( )
1 1 1 1
2 2 2 2
4
4 0 0
4
4 0 0
k
m q k q q q
m
k
m q k q q q
m
+ =  + =
- + =  + =
-
2
2
2
2
1+ 2 +1
1+ 2 +1
1 2 +1
1 2 +1
 
 
1 1
1 1
0.5858 0
3.414 0
k
q q
m
k
q q
m
æ ö
÷
ç
 + =
÷
ç ÷
ç
è ø
æ ö
÷
ç
 + =
÷
ç ÷
ç
è ø


( ) 0!
t + =
 [Θ] q [Λ]q

[ ]
T
Now multiply it by T
( )
( )
& [ [ ]!
T T
é ù
ê ú é ù
ê ú ê ú
= = = =
ê ú ê ú
ë û
ê ú
ê ú
ë û
2
2
1+ 2 +1 0 4 0
Recall [T] [M][T] m [Θ] T] [K][T] k Λ
0 4
0 1- 2 +1
2
1 1 1 1
2
2 2 2 2
0, . . ( )
0, . . ( )
. ., ... (*)
q q i e a SDOF for
i
q t
q q i e a SDOF for q
e gives
t
w
w
+ =
+ =



2
1 1 1
2
2 2 2
( ) ( ) 0
( ) ( ) 0
q t q t
q t q t
of
w
w
+ =
+ =
Solution


i i
A and B
To find the constants , need Initial Conditions :
{ } { } { } { }
{ } { }
( ) ( ) (0) (0)
(0) (0)
t t
=  =
=
Note x [T] q x [T] q
x [T] q


{ } { }
{ } { }
1
1
(0) (0)
(0) (0) !
-
-
=
=
q [T] x
q [T] x
 

1 1 1 1 1
2 2 2 2 2
( ) cos( ) sin( )
( ) cos( ) sin( )
q t A t B t
q t A t B t
w w
w w
= +
= +


Forced Vibration of Undamped MDOF
{ } { } { }
: (t)
Equation of motion [M] x + [K] x f
=

{ } { }
( ) ( )
Take t t
=
Idea : x [T] q
( )
t n t
he +
[M][T]q [ [ =
K T]q f
]

( )
t
T T T
then [T] [M][T]q + [T] [K][T]q [T
= f
]

( )
t
T
then [Θ]q + [Λ]q [T]
= f

1 1
( )
t
- - T
then q + [Θ] [Λ]q [Θ] [T]
= f

1 2
1
is diagonal with diagonal eleme t
(
n s !
is called th
)
e
i
where
t
w
-
-

=
= T
q + [Ω]q [P]
[Ω] [Θ] [Λ]
[P] [Θ] [T] Participation factor matrix
= f

and each is called a
ij
P Participation factor

Meaning of Pij :
Pij gives an indication of how the forcing at the j th mass or node
contribute to the vibration of the ith mode.
1
th
2
e.g., For the i mode's coefficient ,
( ) ( ( )
)
N
i
i i i i j i
j
j
q
q t q P f t F t
w
=
+ =
= å

1 1 2 2 3 3
( ( ( . (
) ) ) )
..
i i i iN N
P f t P f t P f t P f t
= + + + +
{ } { } { } { }
{ }
{ } { }
1 2
1 2
1
1
2
2
With ( ) ( ) ( ) ... ( )
one should note the entire product ( ) represents the 1st mode' contribution,
( ) represents the 2nd mode' contribution, etc to ( )
because the
N
N
t q t q t q t
that q t
q t t
= + + +
ATTENTION :
x η η η
η
η x
{ }
size of depends the chosen normalization of .
i
i
q η

Damped MDOF system under Forced Vibration
{ } { } { } { }
The equation of motion is
+
[M] x [C] x +[K] x f
=
 
:
Solution by modal analysis
{ }
{ } { }
1 2 2
1. Find ... from solving the eigenvalue poblem of [ ]
2. Take ( ) ( )
3. Get [ ... (*)
[
n
t t
w
é ù
= - +
ê ú
ë û
=
+ +
 + +
T T T T
T T
[T] η η η M K η 0
x [T] q
[T] [M][T]q T] [C][T]q [T] [K][T]q [T] f
[Θ]q T] [C][T]q [Λ]q [T] f
=
=
=


1 1 1
[
- - -
 + +
T T
q [Θ] T] [C][T]q [Θ] [Λ] f
=
q [Θ] [T]


[ ] [ ]
[ ] [ ] [ ]
1
1
0
( ) ..... (*)
( ) ( ) ..... (**)
N
j
j
a
b
a b
-
-
=
= +
= å
Particulardamping forms that work :
[C] M K Rayleigh Damping
[C] M M K Caughey damping
1 1
1
4.
2
Will be diagonal generally? If Yes, can write it as 2
and treat the MDOF as N number of SDOF systems, i.e.,
[ i i
etc
z w
z w
-
é ù
ê ú
ê ú
ê ú
ê ú
ë û
T
T] [C][T]
Key Question :
[Θ]
But the Answer is NO generally.
2
1
2 , 1,2,...,
N
i i i i i i ij j
j
q q q P f i N
z w w
=
+ + = =
å
 

[ ] [ ]
, a b
= +
For Rayleigh Damping [C] M K
[ ]
[ ]
1 1
[ [ [
[ [
then
a
a a
a a
- -
- =
 = =
= =
T T
T
Case 1: Mass proportionaldamping [C] M
T] [C][T] T] M [T] Θ]
[Θ] T] [C][T] [Θ] Θ] [I]
[ ]
[ ]
1 1
[ [ [
[ [ ....(**)
then
b
b b
b b
- -
- =
 = =
= =
T T
T
Case 2 : Stiffness proportionaldamping[C] K
T] [C][T] T] K [T] Λ]
[Θ] T] [C][T] [Θ] Λ] [Ω]
Equating to the diagonal matrix of 2 ,
2
2
i i
i i i
i
a z w
a
a z w z
w
 =  =
[I]
2
Equating to the diagonal matrix of 2 ,
one gets 2
2
i i
i
i i i i
b z w
bw
b w z w z
=  =
[Ω]

[ ]
[ ]
2 2
i
i
i
a b
bw
a
z
w
= +
= +
Rayleigh damping Case with [C] M K gives
Modal damping ratio
Note the difference in frequency dependency

[ ]
[ ]
[ ]
[ ] 1
1 2 ...
)
is the
(
N
i i i ij j
j
N
o
wher
r
q q q P
e
f
=
ààà
+ + =
=
å
-1 1
T T
i i i i
T T
i i i i
T - T
[P] = [Θ] [T] [Θ] [ ] Partcipation Factor matrix
η C η η K η
η M η η M η
η η η
 
[ ]
[ ]
[ ]
[ ] [ ]
( )
)
1,2,.., (
i i i
q q q i N
e à
+ àà
+ = =
T T T
i i i i i
T T T
i i i i i i
η C η η K η η f
η M η
N
η M η η M
ot that can also be written as
η
 
1 1 1
[ ( )
- - -
+ + à
T T
q [Θ] T] [C][T]q [Θ] [Λ]q [Θ] [T]
= f
 
Modal form of governing equations for MDOF:

23
Importance of Modal Decomposition in dynamic analysis
• One can choose/select only modes that are important to analyze (e.g., the lower modes in earthquake
problems)
• Can use larger time steps in using direct step-by-step integration methods (for stability and accuracy)
• Without the modal reduction analytically, small time steps will be needed as all higher modes esp. for
a complicated numerical model, are automatically included in the integration but high accuracy is
not quaranteed .
• Artificial numerical damping is thus often employed to damped out high frequency componentwsies

24
Particular Example: MDOF structures subject to Earthquake base motion

{ } { } { } { }
Recall the general equation of motion for MDOF is:
+
[M] x [C] x +[K] x f
=
 
{ } { }
( )
a =
Adaptation to earthquake ground motionproblem?
f 0
{ } { } { } { }
1
1
( )
1
1
ground
b x where
ì ü
ï ï
ï ï
ï ï
ï ï
ï ï
=í ý
ï ï
ï ï
ï ï
ï ï
ï ï
î þ
abs
x = x + 1 1
  
{ } { } { } { } { }
MDOF equation of motion for ground motion is
( ) !
ground
x t effectively
+ =
-
[M] x [C] x +[K] x [M] 1 f
=
  

{ } { } { } { }
With the Equation of motion for MDOF due to base ground motion
ground
x
-
+
[M] x [C] x +[K] x [
= M] 1
  
[ ]{ }
[ ]
2
2 ( )
i i i i i i grou
i i
nd
o q q q x t w ere
r h
V w w a a
æ ö
÷
ç ÷
- ç ÷
ç ÷
÷
=
ç
è
+
ø
T
i
T
i i
η M 1
+ =
η M η
  
{ }
2 1
!
then by the modal decomposition via , one gets
2 ( )
i i i ground
x t
V w w -
+ + = =-
T
x = Tq
q [ ]q [ ]q [Θ] [T] f [P]f [P] ]
= [M 1
  
[ ]
can be diagonalized by the modal shape/modal matrix ,
and assuming [C] T
[ ]
[ ]
[ ]
[ ]
[ ]{ }
[ ]
1 1 2
... , then one can w
,
r
1,2,. ,
ite
( ) ..
o
i i i
N
gr und
M
q q q i N
and
x t
-
-
é ù
= =
æ ö
÷
ç ÷
+ + = ç =
û
÷
ê ú
ë
ç ÷
÷
ç
è ø
T T T
i i
T
i i i
T T T
i i i i i
T
T
i
Recall the Participation facto
η
r matrix i
η C η K η η 1
η M η η M η η M
s
[P] [Θ] [T] [T] η η η
η
  

as the “Seismic
participation factor”

[ ]{ }
[ ]
:
i
i
i i w
a
a
æ ö
÷
ç ÷
ç ÷
ç ÷
÷
ç
è ø
=
T
i
T
i i
Variation of
η M
as a function of or
1
η M η
typically becomes smaller and smaller
at larger and larger natural frequencies .
i
i
numerically
a
w
General observation :
Reason why?

Response spectrum method for MDOF:
2
from solving
2 ( ) ( )
is g
by the response s
.
pectrum, the max
r
ive
response of
a
n by (
( )
due to particu
, )
la
n n ground ground
n
x x
t
x x t x t
x
V w w
w V
-
+
d
R
+
the spectral d
a
isplace
l
ment S
ec l
=
   
[ ]{ }
[ ]
2
Now, in a modal decomposition, the modal coefficient of each mode is gove
(
rned by
2 )
i
i i i i i i gr d
i i
oun
q
q q q x t where
V w a a
w
æ ö
÷
ç ÷
- ç ÷
ç ÷
÷
è
+ =
ç ø
T
i
T
i i
η M 1
=
η M η
+
  
max
the maximum c h
an be given b ( , ) for eac mode !
y = i
i i i
i
q q w V
a
 d
S
How about the maximum value of xi ?

{ } { } { } { }
{ }
1 2
1 2
th
1 2
we defined ( ) ( ) ( ) ... ( ) .
1. the max response of the i mode depends also on the normalization of the
2.the maximums ( ), ( ), ... typically occur at different time
Max
N
N
i
i
t q t q t q t
of q t q t
x q
= + + +
£
R x η η η
η
ecall
Note :
max
1 2
1 max 2 max ... . .
N
i i N i
q q i e RHS is generally an over estimation
h h h
+ + + -
A more optimal and commonly used maximum's estimate is by the " rule":
SRSS
max
1 2 2 2 2
1 max 2 max
max ( ) ( ) ... ( )
N
i i i N i
x q q q
h h h
+ + +


Frequency Domain Analysis of MDOFs
2
)
By modal decomposition, it has been shown that each m
2
ode is g
(
overned by
i i i i i i i
q q q x t
V w w a
+ -
+ =
  
 
2 2
2 2
( )
( )
( )
( ) ( ) ,
( ) )
)
2 (
(
2
i i i ground
ground
i i i
i t
i i i
i i
i
i
q q t e dt as the Fourier tran
q
x
form of q t
then i q
i
x




   

  




 





    
 

  
 
 




 


Define the Fourier transform
 
2
/ / 2
( ) ( ( (
) )
2
)
ground ground
i i i
i q r
a g ound
i i
q a
i
o
e
r
x er
i
wh
q H H


  

   

 

 

 
 
 
 

2
( ) ( )
& & ( )
( )
i i i i
q q
i
q i q
 
 
 
 
   

[ ] { } { } { } { }
1 2
1 2
1
( ) ( ) ( ) ( ) ... ( ) ( )
N
N i
N i
i
t t q t q t q t q w
=
= = + + + = å
Recall x T q η η η η
[ ] { } { } { }
1 2
1 2
( ) ( ) ( )( ) ( ) ... ( ) N
N
q t q q
w w w w w
 = = + + +
x T q η η η

   
{ } { } { }
1 1 2 2
/ / /
( ) ( ) ... ( ) ( )
ground ground ground
N N
q a q a q a x
w w w w
é ù
= + + + ⋅
ê ú
ë û
H η H η H η 

{ }
/
1
( ) ( )
ground
N
i i
q a
i
x
w w
=
é ù
ê ú
= ⋅
ê ú
ë û
å H η 

 
/ 2 2
)
(
2
ground
q a
i
i
i i
i
where
i
H
  




 

 

 
 
 

[ ] { } { } { }
1 2
1 2
( ) ( ) ( )( ) ( ) ... ( ) N
N
q t q q
w w w w w
 = = + + +
x T q η η η

   
{ } { } { }
1 1 2 2
/ / /
( ) ( ) ... ( ) ( )
ground ground ground
N N
q a q a q a x
w w w w
é ù
= + + + ⋅
ê ú
ë û
H η H η H η 

{ }
/
1
,
( ) ( ) ( )
ground
N
i i
q a
i
Concisely
x
w w w
=
é ù
ê ú
=
ê ú
ë û
å
x H η 



Recall g g
x in MDOF x
= =  = =
absolute absolute absolute absolute
Absolute Accelerationsin MDOF :
a x x +1 a x x +1
  
      
1
. .
N
j
j
j
Good to expand in terms of
i e a
=
= å
i
1 η
1 η
Idea? Pre-multiply bothside by ?
i T
η M
1
. .
N
i T j
j
j
i e a
=
= å
T
η M1 η Mη

!
i
j i i
same as the seismic participation factor
a =
T
T
η M1
η M η

( )
1 1 1
( ) ( )
g
N N N
i i i
i i g i i g
i i i
x
q x q x
w w
a a
= = =
+ +
= =
æ ö
÷
ç
= =
÷
ç ÷
ç ÷
è ø
å å å
absolute absolute
a x x +1
η η η
  
   
   
   
2
Recall 2
i i i i i i ground
i
q q q x
V w w a
-
+ + =
  
2 2
2 (2 ) !
i g i i i i i i i i i
i
q x i q q i q
V
a w w w V w w w
 + =- - =- +
 
    
2
2
i g i i i i i
i
q x q q
V w
a w
 + =- -
  
  /
2 2
( ) ( ) ( ) ( )!
Note that solution for all are similar to the1-dof system's solution, i.e.,
1
( ) 2 g
i
g x x g
n n
q
x x x
i
H
   
   
 
 
 
  
 
 
 
 


 
  

 
2
/ / 2
( )
Recallwe had ) ) )
( ( (
2
ground ground
ground
i i i
i q
i
a a
i i
q
q i
i
x w th
H H


 
  

 

 

 

 
 
 

 
( )
2
2
/
2
2 2
2
(2 )( ( ( )
(2 )
)
)
(
)
2
ground
i ground i i i i i
i i i ground
i i i
ground
i
i
i
i
q a
i
i
q x i q q
i x
i
x
i
V w w w
V w w w
V w w w
w w V
w w
w
a
a
w
w
 + =- -
=- +
+ ö
æ ÷
ç ÷
ç ÷
ç ÷
ç ÷
- + ÷
ç ø
=
è
H
 
   




( )
( )
2
2
1
2
1
( )
(2 )
)
(
2
i i i
ground
i
N N
i i
i
i g
i i
i i i
q x
i
i
x
w
V w w w
w w w
w
a
V
a w
= =
+
æ ö
æ ö ÷
ç ÷
ç ÷
÷
ç ç ÷
= = ÷
ç ç ÷
÷
ç ç ÷
÷
- + ÷
ç ÷
ç è ø ø
+
è
å å
absolute
a η η 

 
  

( )
( )
( )
{ }
1
2
2 2
2
/ 2 2
1 1
( )
(2 )
(
2
(2 )
where
2
is the vector-va
)
ground
N N
i i
o
i i i
ground
i i
i
i i g
i i
N
i
i
i
md f i i i
a a
i i i
i
q x
i
i
i
x
i
w
V w w w
w w V w
V w w
a
w
w w V
a
w
a
w
w
w
= =
=
+
æ ö
æ ö ÷
ç ÷
ç ÷
÷
ç ç ÷
= = ÷
ç ç ÷
÷
ç ç ÷
÷
- + ÷
ç ÷
ç è ø
è ø
æ ö
÷
ç ÷
ç ÷
ç ÷
ç ÷
- + ÷
ç
è ø
+
+
=
å å
å
absolute
H
a η η
η
 


  
lued transfer function for a MDOF.
( )
{ }
( )
{ }
( )
{ }
2
2
/ 2 2
2 2
1 1 1 2 2 2
2 2 2 2
1
2
1
1
1 2
1 1 2 2 2
(
2
2 )
2
(2 ) (2 )
2
,
2
ground
mdof i i
i
i
i
i
a
i i
i
a
For a DOF as example
i
i
i
i
i
i
a
w
w
V w w
w w V w
V w w w V w w w
w w V w w w V w
a a
w w
=
æ ö
+
÷
ç ÷
ç ÷
ç ÷
ç ÷
- + ÷
ç
è ø
æ ö æ ö
÷ ÷
ç ç
÷ ÷
ç ç
= +
÷ ÷
ç ç
÷ ÷
ç ç
÷ ÷
- + - +
÷ ÷
ç ç
è ø è
+
=
ø
+
å η
η η
H

( )
Typical profiles of transfer functions H
for MDOFsystems in the frequency domain
w

Dynamics of Continuous System
 Lumped‐mass models (SDOF, MDOF) are inherently an
approximation to many physical systems.
 In geotechnical engineering, the soil region supporting a
building or bridge is inherently a continuous (3D) domain.
 In structural and mechanical engineering:
plate/shell/dome structures,…
 In foundation engineering: earth dams, embankments ….

Multi-D-O-F system  Continuum systems
2

3
Consider a soil or solid stratum/layering
in pure horizontal or simple shear motion y(x,t):
=
x
2
2
y
dx in free vibration
t
r
¶
¶
d
t t
+
t
G, ρ
dx H
( )
2
2
( )
y
a Equation of Motion d dx
t
t t t r
¶
 + - =
¶
2
2
...... (1)
y
Dividing by dx
x t
t
r
¶ ¶
 =
¶ ¶
( ) :
...... (2)
b Constitutive relation for shear deformation
G
t g
=

( ) :
................ (3)
c Strain displacement relation for shear deformation
y
x
g
-
¶
=
¶
2
2
...... (1) ...... (2)
y
Together with and G
x t
t
r t g
¶ ¶
= =
¶ ¶
one gets
2
2
( ) ......... (*)
y y
G
x x t
r
¶ ¶ ¶
=
¶ ¶ ¶
For a homogeneous and medium in free vibration,
G r
2 2
2
2 2
........ 1D classical
........
s
s
y y
C
x t
G
with C
r
¶ ¶
=
¶ ¶
=
Wave Equation
shear - wave speed
2 2
2 2
, ( )
y G y y
Generally G
x x x t
r
¶ ¶ ¶ ¶
 + =
¶ ¶ ¶ ¶

2 2
2 2
( )
g
y y
G y t
x t
r
æ ö
¶ ¶ ÷
ç ÷
 = +
ç ÷
ç ÷
ç
¶ ¶
è ø

( ) ?
g
y t
Case of Horizontal Earthquake GroundMotion Acceleration 
2 2
2
2 2
:
0
( )
s
g
Summary
y y
C
y t
x t
the equation of motion for free vibration or forced vibration
of a soil layer inhorizontal shear motion
ì
ï
¶ ¶ ï
- = í
ï
¶ ¶ ï
î


0: (0, ) 0 .
: ( , ) 0
At x y t fixed base condition
At x h H t traction free top surface condition
t
= =
= = -
a) Boundary conditions :
2 2
2
2 2
( ) ( : find the basic dynamic characteristics)
Equation of motion: 0
subject to the above boundary conditions
s
I purpose
y y
C
x t
¶ ¶
- =
¶ ¶
Free - Vibration Case
0 0
0: ( ,0) ( ) ( ,0) ( )
At t y x y x and y x y x
= = =
b) Initial conditions :
 
Assume steady-state motion
Approach :

2 2 2
2 2 2
2 2 2
2
2
2
Assume steady-state motion, i.e. take ( , ) ( )
( )
0 ( ) 0
0.
i t
s s
s
y x t X x e
y y d X x
C becomes C X x
x t dx
d X
X
dx C
w
w
w
=
¶ ¶
 - = + =
¶ ¶
æ ö
÷
ç ÷
 + =
ç ÷
ç ÷
ç
è ø
Approach :
( ) sin cos for some constants A and B.
s s
X x A x B x
C C
w w
æ ö æ ö
÷ ÷
ç ç
÷ ÷
= +
ç ç
÷ ÷
ç ç
÷ ÷
ç ç
è ø è ø
Solution :
Apply Boundary conditions :
( ) @ 0: (0, ) 0 0 sin 0 cos 0 ( ) sin
s s s
i x y t A B B X x A x
C C C
w w w
æ ö æ ö æ ö
÷ ÷ ÷
ç ç ç
÷ ÷ ÷
= =  = + =  =
ç ç ç
÷ ÷ ÷
ç ç ç
÷ ÷ ÷
ç ç ç
è ø è ø è ø
( )@ : ( , ) 0 (0) cos cos 0
s s
X
ii x H H t G G A H H
x C C
w w
t
æ ö
æ ö æ ö
¶ ÷
ç ÷ ÷
ç ç
÷
÷ ÷
= =  = ç  =
ç ç
÷
÷ ÷
ç ç ç
÷
÷ ÷
ç ç
÷
ç
¶ è ø è ø
è ø

cos 0 ...... (*)
Characteristic/Eigen equation .
s
H
C
is the on the frequency
w
w
æ ö
÷
ç ÷=
ç ÷
ç ÷
ç
è ø
3 5 (2 1)
, , ,.. , 1,2,....
2 2 2 2
s
H i
i giving
C
w p p p p
-
= = =
Implication :
(2 1), 1, 2, ....
2
as the naturalfrequencies of the homogeneous soil layer in shear motion
s
i
C
i i
H
p
w = - =
: ( ) sin sin (2 1) ,
2
i
i
s
x x
Mode Shapes X x i
C H
w p
æ ö æ ö
÷
ç ÷
ç
÷
= = -
ç ÷
ç
÷ ÷
ç ç
÷
ç è ø
è ø

1 1
2 1 2
3 1 2
(2 1),
2
as the frequency & ( ) sin ,
2 2
3
3 as the 2 frequency & ( ) sin ,
2
5
5 as the 3 frequency & ( ) sin
2
s
i
s
C
With i it means
H
C x
fundamental natural X x
H H
x
nd natural X x
H
x
rd natural X x
H
p
w
p p
w
p
w w
p
w w
= -
æ ö
÷
ç
= = ÷
ç ÷
ç
è ø
æ ö
÷
ç
= = ÷
ç ÷
ç
è ø
æ ö
ç
= = ç
ç
è
...... for a stratum.
÷
÷
÷
ø
homogeneous

3 6
1 1
1
: 100', 100 / , 0.25 10
283.7 / sec
2
4.457 / sec 1.41sec
s
Example Homogeneous soil layer H g lb t G psi
G
C ft
rad T
r
r
p
w
w
= = = ´
 = =
 =  = =

:
Forced Vibration due to ground motion
1
2
2
1
2
2
1
:
( , ) ( ) ( )
( ) ( )
( ) ( )
i i
i
i i
i
i i
i
Let y x t q t X x
y
q t X x
x
y
q t X x
t
=
=
=
¥
¥
¥
=
¶
¢¢
 =
¶
¶
 =
¶
å
å
å
Modal expansion approach

2 2
0
for all mode shapes
i i
i i i i
s s
X X X X
C C
w w
æ ö æ ö
÷ ÷
ç ç
¢¢ ¢¢
÷ ÷
+ =  =-
ç ç
÷ ÷
ç ç
÷ ÷
ç ç
è ø è ø

2
1
( ) ( )
i
i i
i s
q t X x
C
w
=
¥ æ ö
÷
ç ÷
=- ç ÷
ç ÷
ç
è ø
å

2 2
2
2 2
( )
s g
y y
C y t
x t
¶ ¶
- = 
¶ ¶

2
1 1
2
1
( ) ( ) ( ) ( ) ( )
( ) ( ) ( ) ( )
i
i i i i g
i i
s
i
i i i g
i s
q t X x q t X x y t
C
q t q t X x y t
C
w
w
= =
=
¥ ¥
¥
æ ö
÷
ç ÷
- - =
ç ÷
ç ÷
ç
è ø
æ ö
æ ö ÷
ç ÷
ç ÷
ç ÷
 + =-
÷
ç
ç ÷ ÷
ç
ç ÷
ç ÷
è ø ÷
ç
è ø
å å
å
 
 

i j
Orthogonality of X and X :
2
How? From 0
i
i i
s
X X
C
w
æ ö
÷
ç
¢¢ ÷
+ =
ç ÷
ç ÷
ç
è ø
2
0
0
0 0
0 .... (1)
H
i
i i j
s
H H
H
i j i j i j
Consider X X X dx
C
and X X dx X X X X dx
w
æ ö
æ ö ÷
ç ÷
ç ÷
ç ¢¢ ÷
+ =
÷
ç
ç ÷ ÷
ç
ç ÷
ç ÷
è ø ÷
ç
è ø
¢¢ ¢ ¢ ¢
= -
ò
ò ò
2
0
0
0 0
0 ...... (2)
H
i
j j i
s
H H
H
j i j i j i
Likewise X X X dx
C
and X X dx X X X X dx
w
æ ö
æ ö ÷
ç ÷
ç ÷
ç ¢¢ ÷
+ =
÷
ç
ç ÷ ÷
ç
ç ÷
ç ÷
è ø ÷
ç
è ø
¢ ¢ ¢ ¢ ¢
= -
ò
ò ò
0
( ) ( ) 0
H
i j
X x X x dx if i j
= ¹
ò
0
& 0
H
i j
X X
¢ =

2
1
0
2
0 0
( ) ( ) ( ) ( )
( ) !
( ) ( ) ( ) ( ) ( ) ( )
j
j j j g
i s
H
i
H H
i
i i i i g i
s
Then take q t q t X x y t
C
and multipleby X x dx and
q t q t X x X x dx y t X x dx
C
w
w
=
¥ æ ö
æ ö ÷
ç ÷
ç ÷
ç ÷
+ =-
÷
ç
ç ÷ ÷
ç
ç ÷
ç ÷
è ø ÷
ç
è ø
æ ö
æ ö ÷
ç æ ö
÷
ç ÷
ç ÷
ç
÷
 + =-
÷
ç
ç ÷
÷ ç ÷
÷
ç è ø
ç ÷
ç ÷
è ø ÷
ç
è ø
å
ò
ò ò
 
 
2
0
2
0
( )
( ) ( ) ( )
( )
4
( )
(2 1)
H
i
i
i i g H
s
i
i g i
X x dx
q t q t y t
C X x dx
y t where
i
w
a a
p
æ ö
÷
ç ÷
 + =-
ç ÷
ç æ ö
÷
ç
è ø ÷
ç ÷
ç ÷
è ø
=- =
-
ò
ò
 


Damping:
:
: , ...
G or E c
t g V g s e e
= + = +
Theory of Viscoelasticity
Kelvin - Voigt 

k
c
Maxwell :
G
t t
g
V
= +



2
2
( ) Equation ofMotion ...... (1)
y
a
x t
t
r
¶ ¶
=
¶ ¶
( ) Constitutive relation for viscoelastic model in shear deformation:
...... (2)
b
G
t g V g
= + 
( ) :
................ (3)
c Strain displacement relation for shear deformation
y
x
g
-
¶
=
¶
2 3 2
2 2 2
(1),(2) (3),
0
......... (*)
( )
g
Combining and the equation of motion with viscous damping is
y y y
G
y t
x x t t
V r
r
ì ü
ï ï
¶ ¶ ¶ ï ï
+ - = í ý
ï ï
¶ ¶ ¶ ¶ ï ï
î þ

: ( , ) ( ) ( )
... modal decomposition
or method of separation of variables in p.d.e.s
Take y x t q t X x
idea of
=
Solution

2 3 2
2 2 2
2
2
(*)
0
( )
0
......... (**)
( )
( ) ( ),
0
( )
g
S
g
S
g
Then leads to
G y y y
y t
x x t t
C q X q X q X
y t
Dividing by T t X x
X q X q
C
y t
X q X q
V
r r
V
r
V
r
ì ü
ï ï
¶ ¶ ¶ ï ï
+ - = í ý
ï ï
¶ ¶ ¶ ¶ ï ï
î þ
ì ü
ï ï
ï ï
¢¢ ¢¢
⋅ + ⋅ - ⋅ = í ý
ï ï
ï ï
î þ
ì ü
ï ï
¢¢ ¢¢ ï ï
+ ⋅ - =í ý
ï ï
ï ï
î þ

 

 


2
2
2
2
2
0 .... ( ) ( :1st term is a function of x only.
constant, say= ....( ),
( ) 0
with the boundary conditions of (0) 0 ( ) 0.
S
S
S
X q X q
C Note
X q X q
X
Taking
X C
then X X
C
X and X H
V
r
w
w
¢¢ ¢¢
+ ⋅ - = 
¢¢
= - 
¢¢
  + =
¢
= =
For free vibration :
 
Recall we found
(2 1) ( ) sin sin (2 1) 1, 2, ....
2 2
for a homogeneous soil layer in shear motion
s i
i i
s
C x x
i and X x i for i
H C H
p w p
w
æ ö æ ö
÷
ç ÷
ç
÷
= - = = - =
ç ÷
ç
÷ ÷
ç ç
÷
ç è ø
è ø

2
2 2
2
2 mode ,
2 2
2 0
.... mode free vibration !
i i i
i i i
S S i
i i i i i
th
Setting which increases with number
C C G
q q q
a damped SDOF equation for i in
w V w V w
V
V w V
r r
V w w
æ ö
÷
ç ÷
=  = =
ç ÷
ç ÷
ç
è ø
 + + =
 
2 2
2 2
2 2
( ),
( ) 0 0 ..... (***)
S S
With
q q
q q q
q q C C
V w V w
w w
r r

æ ö æ ö
÷ ÷
ç ç
÷ ÷
  + ⋅ + =  + + =
ç ç
÷ ÷
ç ç
÷ ÷
ç ç
è ø è ø
 
 

2
,
the governing equation
2 ( ) with the extra damping term
4
with for the homgeneous soil case.
(2 1)
i i i i i j g
i
becomes
q q q y t
i
V w w a
a
p
+ + =-
=
-
For the earthquake ground motion problem
  
(2 1), 1, 2, .... naturalfrequencies
2
s
i
C
i i
H
p
w = - =
( ) sin sin (2 1) , ...
2
i
i
s
x x
X x i mode shapes
C H
w p
æ ö æ ö
÷
ç ÷
ç
÷
= = -
ç ÷
ç
÷ ÷
ç ç
÷
ç è ø
è ø

v
1
max
Recall for a homogeneous layer,
( , ) 4
with (2 1)
(2 1)
i i
i j i i
i
S
q and i
i
w z
a a w w
w p
= = = -
-
:
Example : Modal contribution to response quantities by R
Applications and insights from Ex
esponse Spectrum :
act Solutions
v v
2
max max
1 1
v
2 2
( , ) ( , )
4 4
( , ) ( ) (1)
(2 1) (2 1) (2 1)
4 ( , ) 1 1 1 1
~ 1, , , ...
(2 1) (2 1) 9 25
i i i i
i i i
i i
S S
y H t q X H
i i i
S
where
i i
w z w z
p w pw
w z
pw
æ ö æ ö
æ ö ÷ ÷
÷ç ç
ç ÷ ÷
 = = ÷ =
ç ç
ç ÷ ÷
÷ç ç
ç ÷
ç ÷ ÷
ç ç
- - -
è øè ø è ø
æ öæ ö
÷ ÷
ç ç
÷ ÷ =
ç ç
÷ ÷
ç ç ÷
÷ç
ç - -
è ø
è ø
1
max a v
Similarly,
4
( , ) ( , ) ( , )
i j i i i i
a H t S S
w
a w z w z
p
= = 1

Note: there are now 2 regimes of dynamic behavior:
depending on whether  is > or < than cutcoff

( )
1 1
( , ) ( ) ( ) ( )
2 2
x ct
x ct
y x t f x c t f x c t g d
c
h h
+
-
= - + + + ò

Basic Wave Propagation Theory
in 3D for Soil Dynamics & Seismology
R. Y. S. Pak

2
Homogeneous & isotropic with 2 elastic constants ( )
1 2
Based on (i) Newton'slaw, (ii) stress-strain relationship & (iii) small strain theory
(Navier's equation):
( 2 )
G
and G
G

 


Equationof motion
- =
-
-
-
+
( )
2
1 2 3
, ,
2
2 2
2
( ) ( )
( ) ( )
In rectangular coordinates with , , ,Navier's equation becomes
( ) ,
( ) , (repeated index
k ki i kk i
i
k i
k i k k
i 1,2,3
i 1,2,3
G
or G G
u u u
G u Gu u
u
u u
G G
x x x x t

 
 
 
u u u
u u u
u
=
=
 ⋅ - ´ ´ =
+  ⋅ +  =
=
+ + =
¶
¶ ¶
 + + =
¶ ¶ ¶ ¶ ¶



3
1
2
2 2
3 3
2
1 1
,
)
( )
k
i
k i
k k
k i k k
i 1,2,3
u
u u
G G
x x x x t
 
=
= =
=

¶
¶ ¶
 + + =
¶ ¶ ¶ ¶ ¶
å
å å
Formulation for 2D/3D Soil Dynamics and SSI Problems
12
13 11

 

1 1 2 3
2
. ., sin ( ) , 0
d
d
e g u A x C t u u
L

 
   
 
 
• a sinusoidal plane compressional/dilatational or P-wave train of wave length Ld
• a solution of the Navier’s eqn of motion
2 1 1 3
2
. ., sin ( ) , 0
s
S
e g u A x C t u u
L

 
   
 
 
• a sinusoidal plane shear or S-wave train of wave length Ls
• a solution of Navier’s eqn of motion
Examples: Plane waves solutions:
x2
x1
x3
with ... shear wave speed
s
G
C

=
2
with ... compressional/dilatational wave speed
d
G
C


+
=

3 2
1
2 3
1 2 3
3
1
2 3, 2
1 2 3 1 2 3 3 1
1 2 3 2 1
3
1 1
2
x x
where
x x x x x x x x
x x
 


  

    
 
 
 
 
 
 
 


     
        
 
       
 
 
 

 
 
 
1
e
e e e
e e e ψ e
e
subject to boundary, initial and loading conditions
General Solution by Method of Potentials:
Take 
   
u ψ
2 2
2 2
2 2 2 2
2 2 2
2
2 2 2
1 2 3
Then Navier's equation becomes
1 1
, ( ave equations in 3D)
with
d s
w
C t C t
x x x


 
   
 
  
   
  
ψ
ψ

Plane waves propagating in arbitrary 3D directions:
In terms of the 2 potential functions:
( ) ( , ) ( ) ( , ) ( )
. ., is the direction of the unit vector which denotes the direction of wave propagation
with compressional/dilatational wave speed ... i.e. a P-wav
d d
d
a x t f C t x t f C t
ie
C
d d d
d
k x u k k x
u k
  
       
e.
( ) ( , ) ( ) ( , ) ( )
. ., is orthogonal to the unit vector which denotes the direction of wave propagation
with shear wave speed ..... i.e. a S-wave.
The sh
s s
s
b x t C t x t C t
ie
C
s s s
s
ψ g k x u ψ k g k x
u k
Note:

        
ear wave motion can be decomposed into
a Horizontally-polarized (SH) shear wave and a Vertically-polarized (SV) shear wave.

x
Wave propagation direction
SH wave motion (out of plane)
SV wave motion (in‐vertical plane)
z
y

O
x1 or x, u1 or u
x2 or y
u2 or v
x3 or z, u3 or w
2
2
3 2
1
1 2 3
2 1
3
3 1 2
0 ( ):
( )
( )
2
With u and plane strain
x
u u
x x x x z
u w
x x x z x
depend on only scalar potential functions and
 
  
 
  
 



 
  
     
    
 
  
     
    
Simplification for 2D Wave Propagation Problems (Plane Strain):
2 2
2 2
2 2
1 1
,
d s
C t C t
 
 
 
   
 
3 2
1
2 3
1 2 3
3
1
2
1 2 3 3 1
1 2 3 2 1
3
1 1
2
x x
x x x x x
x x
 


    
 
 
 
 
 
 
 


  
    
 
    
 
 
 

 
 
 
e
e e e
ψ e
e

Example: Time harmonic Incident Plane P- and SV-waves
in a Semi-Infinite Soil in 2D (Plane-strain)
n
l

sin 2(1 )
where = , the ratio of compressional to shear wave speed
sin (1 2 )
s d d
d s s
C C
k k
C C

 
  

   

Physical phenomena of wave
reflection, mode conversion,
diffraction, refraction,...

1 2
Other important wave types and solutions of boundary value problems of soil dynamics and
seismological interest:
- Rayleigh waves (a surface wave with motion decaying quickly with depth) with wave speed CR (< CS< Cd)
- Theoretical basis of site/soil characterization by wave-based methods and forced vibration testing
(eg dynamic load on finite area)
- Fundamental to seismic/dynamic soil-structure
- Extension and applications to multi-layer soil configurations
Dynamic foundation response from applied loads
(SSI problems)
Incoming SH wave (simpler than SV wave)
with 1 = 2

Dynamic Soil-Structure Interaction
(551) Problems
ExamDle: A Comoressor Foundation Dynamic Problem
Rigid body dynamics: F=ma, M=Icx
Soil
Soil
e at (0 rad/sec

Needed material information:
Establish soil/site/foundation/structure conditions
•Dynamic loading, nature, magnitudes and directions
•Soil profile: sand, clay, rock, thickness, layering,
•Density, void ratio, P1, OCR,
•Dynamic shear modulus G and damping with their strain
dependence
•Machine’s mass, moment of inertia, stiffness
‘Foundation type, shape, weight/bearing pressure
‘Design criteria
Example: Characterization of dynamic loads
Newton’s law: F= m a, M= ‘M
Mmachine
Soil

Resultant
dynamic loads:
F=me rw2 = m7v2/r
5 to 10% rotating mass
= Fsin(wt) or
F = Fsin(at)
F = FcosQot) F, = Fcos(cot)
Fundamental example problem:
A Rigid footing under dynamic loading
• A Mechanics Contact problem
• 3D elastodynamic theory and wave radiation phenomena
• Interface & boundary conditions
• Concept of radiation damping
• Analytical methods
• Finite element and boundary element methods
• Frequency and time domain
I
i-i I foundation
interface

Foundation Interfacial Impedance Matrix
V K(w) 0
H 0 0
M 0 0
T 0 KTT(co) ®
• From solution of 3D continuum boundary value problems
• In frequency domain / time-harmonic factor ebo)t
• Each function is generally complex-valued for nonzero (0
i.e., K1 (w) = Re[K (w)] + i Im[K (w)]
• ‘Dynamic foundation impedance functions’
• Contact stress distributions
• Horizontal-rocking motion coupling
Note:
1. Notion of ‘Frequency
(*)
dependent’ springs and
dashpots due to 3D wave
propagation phenomena
2. Radiation/geometric
damping
i.e. a mechanical analog of Impedance Functions (suggestion by Lysmer 1965)
0
Khh(o)
Kmh (0)
0
0
Khm (t0)
Kn?m (t0)
0
Recalifrom SDOF with spring-rnass-dasphot:
F(t)=kx(t)+c 1(t) F(o)=kx+kocx =‘F(o)=(k+iwc)x=K(w)x ....(*)
Comparing it with
K(co)=Re[K(w)]+ i Im[K(w)]
one can set
k =Re[K1(o)] =k(w)
c= Jm[K(o)]/w=c(o)
= 2 = Ccriticai

Foundation Interfacial Compliance Matrix
C (w) = Re[C (w)] + i Im[C1 (w)]
- //,‘
*I
‘
C(w) 0 0 0 V
Ah — 0 Chh(w) Chm(W) 0 H
Or — 0 CmhfrO) Cmm(CO) 0 M
°T 0 0 0 CTT(a)) T
• jCJ=[K]’
• Symmetric matrices due to reciprocity property in elastodynamics theory
• Depend on foundation shape, type, embedment, soil profile,
• Examples for circular and square surface foundations:
•
Classical Solution for Foundation Compliance Functions by Homogenous Half-space model:
Notation: a=radius, a=Poisson ratio, i=shear modulus (Luco & Westmann (1971)
16
/I
7
.6 -
__zr— ‘

Square foundation impedance functions by Homogenous Half-space model:
(Pak & Guzina 1999)
Rk SlfCsf of Sqs Sfc, F d.ss
Hp El. H,If-S
k =ic =-
‘ Gb’
hh
Gb
K,
k Kmm
mhGb2 mm
Gb3
r
,‘97Ib!fI3
.i
FIg 0-21 V,siI ,ibSi ( dI f,,Sim. f 4
Fry (1963), Richart, Hall & Woods (1970)
Results from centrifuge model tests
*
Pak et al. (2010) “Physical Characteristics of Dynamic Vertical-Horizontal-Rocking
Response of Surface Foundations on Cohesionless Soils,” Geotechnique
G=shear modulus, v=Poisson ratio, b=half-width
V,s1,,j SifY,p cf a Sql,aa Sda,a F,,,,d.,,,
HopSaCC ElsO, HaJf-0p.a
IC =
CpIi,.g Cf• Sq F,.,,d.U,,
H.
LS,aJ OCtl,,aa,, Sqaa 0IISCS PCCIiII
HCgaC E. Hi1-S
soc. 00.6
Results from experimental field tests
sEC. 0.7 R1XKf3JVIHR4rIoS5 30 FOIJ’4DATIONS 371
0
FI0C,a 0-06. CsopIad sskICga,d .1___i__Ji_..._. so1
,IICjC ,ibIoI,,,a ,f WES Ba,a . 8, 337
I. Taos 36. (a) CI5O5Cs,ao ‘t’ B,’C CI
C 0.33 2C
A,,.,,,

Reasons:
1: In-situ depthwise variation ofshear modulus ofreal soils
(i.e., generally not homogeneous)
e.g., sand, gravel, or NC clay
2: Theoretical vs physical contact stress distributions
small-strain theory
(a)
failure limit
(b)
actual service state
(c)

3: Effects of foundation weight and loading
If
Analytic Resolution by New Elastodynamic 551 Theory
(Pak and Ashlock, EESD 2011)
1.5
0 Depth ratio
E hf/b
0 Modulus ratio
,=
—
0.5
Standard elements
AG elements
2
10
y/a xla

R. Y. S. PAK AND J. C ASHLOCK
—1
0 1 2
cøa / (G0/p)°5
(d)
Vertical, Horizontal, Rocking Foundation Responses
—
— .254.0 14. c1.6
-
y45. c3.2 —j4.5. c1.5
‘ 2, 2.4 -:=5. ‘1.3
.
1=3.5)=19 =1 05
0 500 1000 1500
Frequency [Hzl
500 1000 1500 2000
Frequency 1Hz]
3
0
0
E
E
2’:
2
E
Cu
0
0
rn
1 2
wa I (G0/p)°5
Figure I I. Impedance functions K11() by 2-zone theory with h= I. (a) K,,:
(b) Ku,,: (C) K,,,,,: and (dl K,,,,, and Kh,,,.
/ -H
.-
2000
—
— C=.25.n=4.0 — 0=4. ã=1.6
n=2.5. 2=3.2 : C=4.5. 2=1.5
-0=3. G=2.4 —-0=5. 2=1.3
O 0 .)35. =19 .4=0,2=1.0S
- -.
—b

Mechanical Analogs of Impedance Functions for simplified analysis
F(t)=kx(t)+c±(t) F(do)=kx+iacx
=F(o)=(k+iac)x=K(oi)x ....(*)
Comparing it with
K11(o)=Re[K1(w)]+i [m[K1(eo)]
one can set in (*)
k = Re[K. (w)] = k(to) Note:
U 1. Notion of ‘Frequency-dependent’ springs
c = Im[K1 (w)] / tü = c(a) and dampers (3D wave propagation
phenomena
— C — C 2. Concept of Radiation/geometric
1i damping
4J !W1t critical

Use: Convert differential equations of motion
to simpler algebraic equations:
-1
2
( ):
F[ ( )] ( ) ( )
:
1
F [ ( )] ( )
2
:
F[ ( )] ( ) ( ), F[ ( )] ( ) ( ) , .
i t
i t
Fourier transform of a function f t
f t f t e dt
Inverse Fourier transform
e d
Key properties
f t i f t i etc



  

   





 

 


 
F
F F
F F
Frequency‐Domain Approach:

(1) Vertical vibration:
Time harmonic response,
i.e.
( ) , ( ) ,....
i t i t
F t e t e
 
  
F Δ
Frequency‐domain Dynamic Analysis of Foundations
0 vv 0 0 G
V =K (ω)Δ & Δ =Δ
......(1)
v e o
F V m
   

G

2
v-e o G
F -V =-ω mΔ
=
v
m

v

Fv‐e
V0
2
v-e vv G G
F -K (ω)Δ = -ω mΔ
...(2)
v-e
G 2
vv
F
Δ =
-ω m +K (ω)
଴

(a) Equations of Motion:
x x
F m
 
 
(2) Horiz‐rocking coupled vibration:
 
F ma, M I α
G G
M I

 
G
I 

o
H
= G
m

e
F e
M
G
O
1
2
d
d
2b
o
M
o
H
...............(1)
e o G
F H m
   
 2
e o G
F -H =-ω mΔ
1 2 .....(2)
e e o o G
M F d H d M I
    
 2
e e 1 o 2 o G
M +F d +H d -M =-ω I θ

...(3)
     
 
 
     
 
 
   
     
G o e
2
G o e e 1
2
Δ H F
1 0
m 0
-ω + =
θ M M +F d
-d 1
0 I
(b) Foundation‐soil interfacial impedance relations:
.............(4)
    
   
 
    
o hh hm o
o mh mm o
H K K Δ
=
M K K θ
.............(5)
      
 
 
     
 
 
 
   
      
G hh hm o e
2
G mh mm o e e 1
2
Δ K K Δ F
1 0
m 0
-ω + =
θ K K θ M +F d
-d 1
0 I

(c) Relation between motions at different points :
0
G


G
o


o

o

............(6)
   
 
   
 
 
   
o G G 2
o G
o G
2
o G
Δ =Δ -θ *d
θ =θ
Δ Δ
1 -d
=
θ θ
0 1
2
d

(d) Final equation assembly:
Substituting (6) to (5), one gets
2
( ) .............(7)


 
  
 
M K F
x

0
,
0
m
I
 
  
 
M
2
2
1 0 1
1 0 1
hh hm
mh mm
K K d
K K
d

 
   
  
   
  
   
K

1
, ,
G e
G e e
F
M Fd


   
 
   

   
x F
where
The matrix equation (7) for coupled lateral response motion can be readily
solved for any given loading F .

dynamical analysis of soil and structures

dynamical analysis of soil and structures

Recommended

Recommended

More Related Content

Similar to dynamical analysis of soil and structures

Similar to dynamical analysis of soil and structures (20)

Recently uploaded

Recently uploaded (20)

dynamical analysis of soil and structures