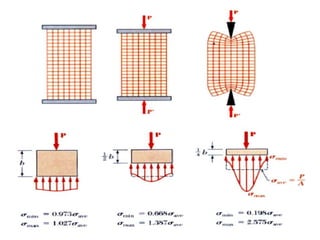
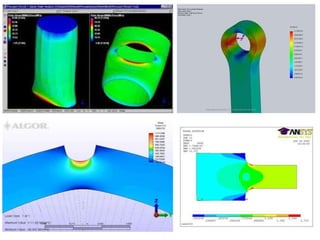
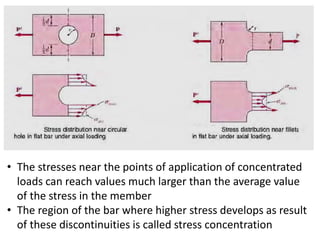
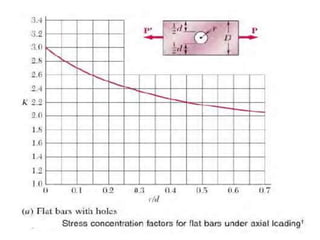
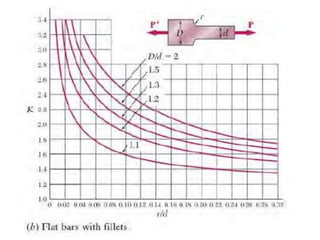
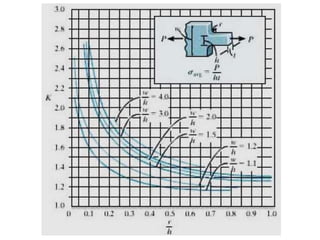
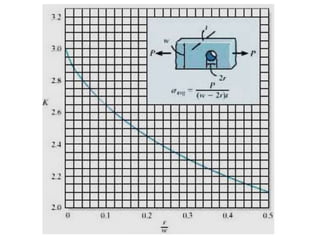
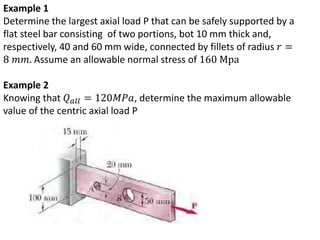
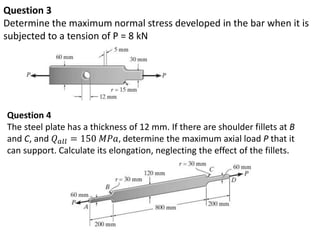
Saint-Venant's principle states that the stresses and strains far away from the load application point are unaffected by the exact nature of the load or its application method, but only depend on the resultant load magnitude and application area. Stress concentrations occur where the cross-sectional area changes abruptly, like holes, notches, or threads, and cause local stress values much higher than the average stress. The stress concentration factor K is used to relate the maximum stress σmax to the average stress σave in a cross-section. Design engineers use stress concentration factors and allowable stress values to determine if a given load will exceed the material's strength at stress concentration locations.

1. MOM 120S
Stress Concentration
Lecture 6
Okorie M.E

2. Saint-Venant's Principle
Saint-Venant's Principle, named after the French elasticity
theorist Adhémar Jean Claude Barré de Saint-Venant can be
stated as saying that: "... the difference between the effects of
two different but statically equivalent loads becomes very small
at sufficiently large distances from load.“
OR
Stress and strain produced at points in a body sufficiently
removed from the region of load application will be the same as
the stress and strain produced by any applied loadings that have
the same statically equivalent resultant,
and are applied to the body within the same region
In other words, the method in which the load is applied does
not affect the stresses at the sufficient distance away from the
load application location

4. Note
• Loads transmitted through rigid plates result in uniform
distribution of stress and strain.
• Concentrated loads result in large stresses in the vicinity
of the load application point

5. Stress Concentration
Definition: A stress concentration (often called stress raisers or stress
risers) is a location in an object where stress is concentrated. An object
is strongest when force is evenly distributed over its area, so a reduction
in area, e.g., caused by a crack, results in a localized increase in stress.
Stress raisers: In reality, bars often have holes, grooves, notches,
keyways, shoulders, threads, or other abrupt changes in geometry that
create a disruption in the otherwise uniform stress pattern. These
discontinuities are called stress raisers

7. • The stresses near the points of application of concentrated
loads can reach values much larger than the average value
of the stress in the member
• The region of the bar where higher stress develops as result
of these discontinuities is called stress concentration

8. Design consideration
• The maximum stress 𝜎 𝑚𝑎𝑥 occurs at the edges of the
hole and may be larger than the normal stress 𝜎 = 𝑃 𝐷𝑡
at the same cross section
• For design consideration, the result obtained depends on
the following: In case of a circular hole in a bar we
consider the ratio 𝒓 𝒅 .For the fillet the ratio is
𝒓 𝒅 𝑎𝑛𝑑 𝑫 𝒅

9. • Again, as design engineers, we are more interested in the
maximum value of the stress in a given section, than in the
actual distribution of stress in the section, since our main
concern is to determine whether the allowable stress will be
exceeded under a given loading, and not where this value will
be exceeded.
• For this reason, we define the ratio 𝑲 =
𝝈 𝒎𝒂𝒙
𝝈 𝒂𝒗𝒆
Where 𝐾 is the stress concentration factor of the given
discontinuity or stress raiser.
Analysis of Stress Concentration
To calculate the maximum value, first do the following
• Calculate the average stress in the critical region 𝝈 𝒂𝒗𝒆 = 𝑷 𝑨
• Multiply the result obtained by the appropriate stress
concentration factor 𝐾

10. NOTE: This procedure is valid only as long as 𝜎 𝑚𝑎𝑥 does not
exceed the proportional limit of the material. Since the value
of K plotted in the graph below were obtained by assuming a
linear relation between stress and strain
How do we obtain the value of K?
• We make use of the graphs below

15. Example 1
Determine the largest axial load P that can be safely supported by a
flat steel bar consisting of two portions, bot 10 mm thick and,
respectively, 40 and 60 mm wide, connected by fillets of radius 𝑟 =
8 𝑚𝑚. Assume an allowable normal stress of 160 Mpa
Example 2
Knowing that 𝑄 𝑎𝑙𝑙 = 120𝑀𝑃𝑎, determine the maximum allowable
value of the centric axial load P

16. Question 3
Determine the maximum normal stress developed in the bar when it is
subjected to a tension of P = 8 kN
Question 4
The steel plate has a thickness of 12 mm. If there are shoulder fillets at B
and C, and 𝑄 𝑎𝑙𝑙 = 150 𝑀𝑃𝑎, determine the maximum axial load P that it
can support. Calculate its elongation, neglecting the effect of the fillets.