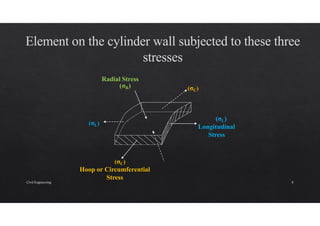
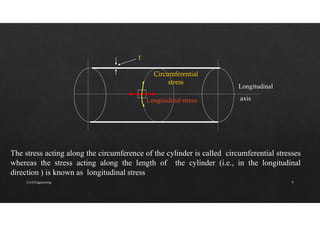
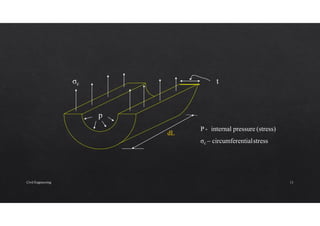
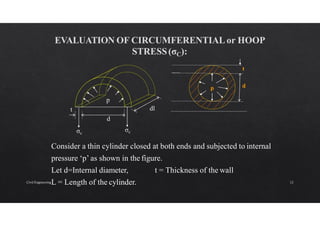
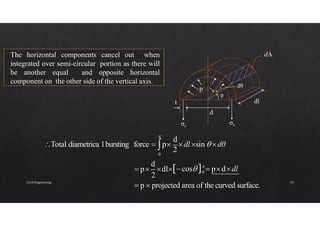
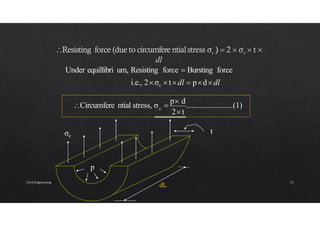
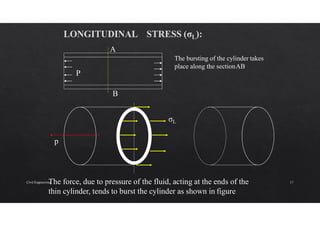
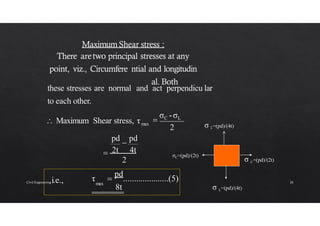
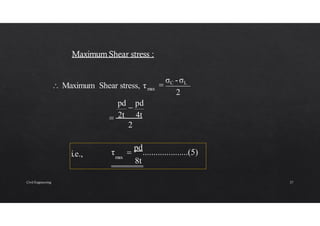
The document discusses the study of stresses and strains in cylindrical shells, specifically differentiating between thin and thick cylinders, their assumptions for analysis, and the calculations involving circumferential and longitudinal stresses. It emphasizes the practical applications of cylinders in engineering, such as pipes and pressure vessels, and incorporates equations and assumptions based on internal pressures and material properties. Moreover, the document addresses methods for evaluating the resulting strains and deformation, concluding with examples and derived formulas for stress analysis.

1. Civil Engineering 1

2. Objectives of Study
1.Define a Cylindrical shell and distinguish between thin and thick
Cylinders
2.Identify the assumptions involved in the analysis of a thin cylinder,
3.Determine the stresses in a thin cylinder
4.Find the strains and deformation in thin cylinder
5.Find stresses in a wire bound pipe
6.Understand concept of Thick Cylinder
Civil Engineering 2

3. Civil Engineering 3

4. INTRODUCTION:
In many engineering applications, cylinders are frequently used for
transporting or storing of liquids, gases or fluids.
Eg: Pipes, Boilers, storage tanks ,Oxygen Cylinder, Spray can etc.
Spherical gas container
Cylindrical pressure
vessel.
Fire Extinguisher with rounded
rectangle pressure vessel
Aerosol
spray can
Civil Engineering 4

5. The following assumptions are made in order to derive the expressions for
the stresses and strains in thin cylinders :
(i) The diameter of the cylinder is more than 20 times the thickness of the
shell.
(ii) The stresses are uniformly distributed through the thickness of the wall.
(iii) The ends of the cylindrical shell are not supported from sides.
Civil Engineering 5

6. Civil Engineering 6

7. p p
p
p
p
p
σC
σC
σC
σC
σL
σL
σL
σL
σR
Hoop or Circumferential
Stress
Longitudinal
Stress
Radial Stress
Civil Engineering 7

8. Hoop or Circumferential
Stress
(σC)
(σC)
(σL)
Longitudinal
Stress
Radial Stress
(σR)
(σL)
Civil Engineering 8

9. Longitudinal
axis
Longitudinal stress
t
The stress acting along the circumference of the cylinder is called circumferential stresses
whereas the stress acting along the length of the cylinder (i.e., in the longitudinal
direction ) is known as longitudinal stress
Civil Engineering 9

10. p
σc σc
P - internal pressure (stress)
σc –circumferentialstress
Civil Engineering 10

11. P - internal pressure (stress)
σc – circumferentialstress
dL
σc
p
t
Civil Engineering 11

12. Consider a thin cylinder closed at both ends and subjected to internal
pressure ‘p’ as shown in the figure.
Let d=Internal diameter, t = Thickness of the wall
L = Length of the cylinder.
p d
t
σc
σc
dl
t
p
d
Civil Engineering 12

13. To determine the Bursting force across the diameter:
Consider a small length ‘dl’ of the cylinder and an elementary
area ‘dA’ as shown in the figure.
x
2
dF  p
d
dlcosθdθ
dA
σc
σc
dl
t
p
d
dθ
θ
Force on the elementary area,
dF  pdA  prdl dθ
 p
d
dl dθ
2
Horizontal component of this force
y
2
dF  p
d
dlsin θdθ
Vertical component of this force
Civil Engineering 13

14. The horizontal components cancel out when
integrated over semi-circular portion as there will
be another equal and opposite horizontal
component on the other side of the vertical axis.
d
0

Total diametrica l bursting force  p
2
dl sin  dθ
dA
σc
σc
dl
t
p
θ
d
dθ
2
d
0
 p  projected area of the curved surface.
 p dl 
cos  pddl
Civil Engineering 14

15. c
2t
Circumfere ntial stress, σ 
p d
........................(1)
dL
σc
p
t
Under equillibri um, Resisting force  Bursting force
i.e., 2σc  tdl  pddl
Civil Engineering 15

16. c
2t
Circumfere ntial stress, σ 
p d
........................(1)
Force due to fluid pressure = p × area on which p is acting = p ×(d ×L)
(bursting force)
Force due to circumferential stress = σc × area on which σc is acting
(resisting force) = σc × ( L × t + L ×t ) = σc × 2 L × t
Under equilibrium bursting force = resisting force
p ×(d ×L) = σc × 2 L ×t
Civil Engineering 16

17. p
σL
The force, due to pressure of the fluid, acting at the ends of the
thin cylinder, tends to burst the cylinder as shown in figure
A
P
B
The bursting of the cylinder takes
place along the sectionAB
Civil Engineering 17

18. EVALUATION OF LONGITUDINAL STRESS (σL):
t
σL
p
Longitudin al bursting force (on the end of cylinder)  p 
π
d2
4
Area of crosssection resisting thisforce  π  d  t
Let σL  Longitudin al stress of thematerialof thecylinder.
Resisting force  σL πdt
Civil Engineering 18

19. L  πdt
i.e., p 
π
 d 2
σ
4
L
4 t
 Longitudin al stress, σ 
p  d
...................( 2)
From eqs (1) & (2), σC  2  σ L
Under equillibrium, bursting force  resisting force
Civil Engineering 19

20. 4
π
L
2
d  σ πdt
i.e., p  ...................( 2)
stress, σL
4t
pd

 Longitudinal
Force due to fluid pressure  p  areaon which p is acting
 p
π
d2
4
Re sisting force  σL  area on which σL is acting
 σL  πd t
circumference
Under equillibri um, bursting force  resisting force
Civil Engineering 20

21. σ C=(pd)/(2t)
σ C=(pd)/(2t)
σL=(pd)/(4t)
σ L=(pd)/(4t)
A point on the surface of thin cylinder is subjected to biaxial stress system, (Hoop
stress and Longitudinal stress) mutually perpendicular to each other, as shown in the figure.
The strains due to these stresses i.e., circumferential and longitudinal are obtained by
applying Hooke’s law and Poisson’s theory for elastic materials.
Civil Engineering 21

22. E
εC
Circumfere ntial strain, εC :
μ 
σL

σC
i.e., εC (2 μ)................................(3)

δd

p d
d 4tE
σ C=(pd)/(2
σC=(pd)/(2t)
L
σ =(pd)/(4t)
L
σ =(pd)/(4t)
Note: Let δd be the change in diameter. Then
d
original circumference
c
d

 
  d d d 

d

final circumference - originalcircumference
E
E
(2 μ)
E

σL
E
 2
σL
μ
σL
Civil Engineering 22

23. E E
εL
Longitudin al strain, εL :
μ 
σC

σL
i.e., εL (12μ)................................(4)

δl

pd
L 4tE
VOLUMETRIC STRAIN,
v
V
Change in volume = δV = final volume – original volume
original volume = V = area of cylindrical shell × length
L

 d 2
4
E E E
(1 2μ)

σL
μ
(2σL )

σL
Civil Engineering 23

24. final volume = final area of cross section × final length
4
4
4

 d2
L  ( d)2
L  2 Ld  d  d 2
 L  ( d)2
 L  2d  d  L

 d2
 ( d)2
 2d  d L L

 d  d2
L L
4
neglectingthesmallerquantitiessuchas ( d)2
L,( d)2
 L and 2 d  d  L
Finalvolume
 d2
L  2 Ld  d  d 2
 L
4
changeinvolumeV 
 d2
L  2 Ld  d  d 2
 L 
 d2
L
4 4
V 
 2L d  d  d 2
 L
Civil Engineering 24

25. V π
 d2
L
dv
 4
L
= ε + 2 × εC
V
dV
i.e., (5 4μ).................(5)
V 4tE
dv

p d
(2 μ)
4tE
pd
(1 2μ)  2
4tE
pd

L d
4

 L
 2 
 d
Civil Engineering 25

26. 2
these stresses are normal and act perpendicu lar
to each other.
max
 2t 4t
2

σC -σL
 Maximum Shear stress, τ
pd

pd
i.e., max
τ 
pd
.....................(5)
8t
C
σ =(pd)/(2t)
C
σ =(pd)/(2t)
σ L=(pd)/(4t)
L
σ =(pd)/(4t)
Civil Engineering 26

27. 2
max
 2t 4t
2

σC -σL
 Maximum Shear stress, τ
pd

pd
i.e., max
τ 
pd
.....................(5)
8t
Civil Engineering 27

28. = 50 N/mm2 = 50 MPa (Tensile).
PROBLEM 1:
A thin cylindrical shell is 3m long and 1m in internal diameter. It is
subjected to internal pressure of 1.2 MPa. If the thickness of the sheet is
12mm, find the circumferential stress, longitudinal stress, changes in
diameter, length and volume . Take E=200 GPa and μ= 0.3.
SOLUTION:
1. Circumferential stress, σC:
σC= (p×d) / (2×t)
= (1.2×1000) / (2× 12)
2. Longitudinal stress, σL:
σL = (p×d) / (4×t)
= σC/2 = 50/2
= 25 N/mm2 = 25 MPa (Tensile).
Civil Engineering 28

29. Change in length = ε L ×L= 5×10-05×3000 = 0.15 mm(Increase).
(2 μ)
(pd)
Change in diameter, δd = εc ×d
= 2.125×10-04×1000 = 0.2125 mm (Increase).
4. Longitudinal strain, εL:
εc 
(4  t)

E

(1.2 1000)

(2  0.3)
(412) 200103
 2.125 10-04
(Increase)
ε 
(pd)

(1 2μ)
L
(4t) E

(1.21000)

(1 20.3)
(412) 200103
 5 10-05
(Increase)
Civil Engineering 29

30. (5 4μ)
V
Volumetric strain,
dv
:
(5 40.3)
(412)200103
(1.21000)

 4.75 10-4
(Increase)
Change involume, dv  4.75 10-4
V
 4.75 10-4

π
10002
3000
4
1.11919106
mm3
1.1191910-3
m3
1.11919 Litres.
Civil Engineering 30

31. Stresses in Thin Spherical Shell
The stress produced in the material is equivalent to the longitudinal stress in the cylinder so
Civil Engineering 31

32. Civil Engineering 32

33. Civil Engineering 33

34. Civil Engineering 34

35. Stresses in Wire winding Thin Cylinder
Civil Engineering 35

36. Civil Engineering 36

37. Civil Engineering 37

38. Civil Engineering 38

39. Civil Engineering 39

40. Stresses in Thick Cylinder
The Analysis of Thick Cylinders is usually based on Lame’s Theory and for wh
assumptions made are as follows:
1.The material of the cylinder is homogeneous and isotropic.
2.The material stressed within elastic limits.
3.Plane sections normal to the longitudinal axis of the cylinder remain plane a
application of pressure.
4.Young’s modulus is the same in tension and compression.
5.All fibres are free to expand or contract under the action of forces irrespective
of adjacent fibres.
Civil Engineering 40

41. Stresses and strain in Thick Cylinder
Three Stresses and strain are developed
1.Radial (compressive)
2.Circumferential (tensile)
3.Longitudinal (tensile)
Civil Engineering 41