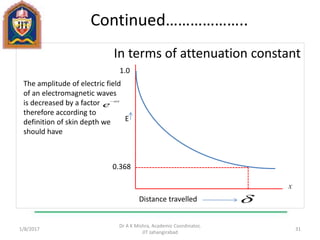
The document discusses Maxwell's equations and fundamental concepts of electromagnetism, including scalar and vector fields, laws of electricity and magnetism, and methods of integration such as Gauss's and Stokes's theorems. It covers key principles such as Gauss's law, Faraday's law of electromagnetic induction, and the equation of continuity, highlighting their significance in the behavior of electric and magnetic fields. Additionally, it addresses the concept of displacement current and the derivation of Maxwell's equations in both differential and integral forms.

1. 1/11/2017 1
Dr A K Mishra, Academic Coordinator,
JIT Jahangirabad
Engineering Physics II
By
Dr. A. K. Mishra
Associate Professor
Jahangirabad Institute of Technology, Barabanki

2. Maxwell`s Equations and Electromagnetic Waves
•Electromagnetism was developed by Michel faraday in 1791-1867and latter
James Clerk Maxwell (1831-1879),put the law of electromagnetism in he form
in which we know today. these laws are called Maxwells equation.
Scalar field: A scalar field is defined as that region of space whose each point
is associated with scalar function ie. A continuous function which gives the
value of a physical quantity like as flux, potential, temperature,etc.
Vector field: A vector field is specified by a continuous vector point function
having magnitude and direction both changes from point to point in given
region of field. The method of presentation of a vector field is called vector
line.
1/11/2017
Dr A K Mishra, Academic Coordinator,
JIT Jahangirabad
2

3. Gradient , Divergence and curl
• The rate of change of scalar and vector fields is denoted by a
common operator called Del,or nebla is used which is written
as
If is a differentiable scalar function, its gradient is
defined as
grad
grad is a vector whose magnitude at any point is equal to
the rate of change of at a point along a normal to the
surface at the point.
1/11/2017
Dr A K Mishra, Academic Coordinator,
JIT Jahangirabad
3
z
k
y
j
x
i










z)y,(x,
  )
z
k
y
j
x
i(








  z
k
y
j
x
i







 



4. Gauss Divergence theorem
(Relation between surface and volume integration )
According to this theorem , the flux of a vector field over any closed
surface S is equal to the volume integral of the divergence of the vector
field over the volume enclosed by the surface S.
1/11/2017
Dr A K Mishra, Academic Coordinator,
JIT Jahangirabad
4
F

)1.....(....................dvFdivsd.
v
 

s
F

5. Stokes Theorem
( Relation between surface and volume integration)
• The surface integral of the curl of a vector
field taken over an surface S is equal to the
line integral of around the closed curve.
1/11/2017
Dr A K Mishra, Academic Coordinator,
JIT Jahangirabad
5
A

A

...(2)....................ld.As.d)Ax(
ld.As.d)ACurl(






s
s

6. Fundamental laws of electricity and
magnetism
• Gauss law of electrostatics
i.e electric flux from a closed surface is equal
to the charge enclosed by the surface.
Gauss law of magnetostatics:
i.e the rate of change of magnetic flux from a
closed surface is always equal to zero.
1/11/2017
Dr A K Mishra, Academic Coordinator,
JIT Jahangirabad
6
(3)....................
q
s.d
0
 


E
 0
1
  .......(4)....................0sd.

B

7. Continued……………..
• Faradays law of electromagnetic induction: the rate of change of
magnetic flux in a closed circuit induces an e.m.f which opposes the
cause,i.e
• Amperes law :
the line integral of magnetic flux is equal to times the current
enclosed by the current loop.
1/11/2017
Dr A K Mishra, Academic Coordinator,
JIT Jahangirabad
7
5).........(....................
d
-
dt
e


.....(6)....................Ild.
0  

B
0

8. Equation of continuity
• Electric current is defined as the rate of flow of charge i.e
If dq charge is enclosed in a volume dv and is leaving a
surface area ds then we have
where J is the current density and is the volume charge
density .therefore eq (1 ) becomes
1/11/2017
Dr A K Mishra, Academic Coordinator,
JIT Jahangirabad
8
....(1)..............................
dt
dq
-i
 
vs
dVqandsd.J 

i


9. Continued……………
1/11/2017
Dr A K Mishra, Academic Coordinator,
JIT Jahangirabad
9
equation.continuitycalledis0
t
J
surfacearbitraryanfor0)dV
t
J(div
dV
t
-dVJdiv
become2equationretherefodVJdiv-sd.
getwe2equationofL.H.Sontheoremdivergencegaususing
2).........(..........dV
t
-sd.
dV
dt
d
-sd.
v
vv
v
v
v


























div
J
J
J
s
s
s




10. Displacement current
• According to Maxwell not only current in the
conductor is Produces a magnetic field but
changing electric field in vacuum or in
dielectric is also Produces a magnetic field.
Means changing electric field is equivalent to
current produces same magnetic effect as A
conventional current in a conductor. This
equivalent current is called displacement
1/11/2017
Dr A K Mishra, Academic Coordinator,
JIT Jahangirabad
10

11. Maxwells Electromagnetic
equations:(diffrantial form)
1/11/2017
Dr A K Mishra, Academic Coordinator,
JIT Jahangirabad
11
densityCharge
nal)(conventiodensityCurrentJ
intensityfieldMagneticB
intensityfieldElectricE
nt vectordisplacemeElectricD
where
t
D
JHCurlor
t
D
JH.
t
-ECurlor
t
-E.
0BDivor0B.
DDivor.
































BB
D

12. Maxwell's Electromagnetic
equations:(Integral form)
1/11/2017
Dr A K Mishra, Academic Coordinator,
JIT Jahangirabad
12

 

 








meaningusualtheirhavesymbolss.dB
t
-ld.
S.d)
t
D
J(.
0sd.
.dsDordvsd.
s
s
sv






E
ldH
B
D
s


13. Derivation of Maxwells Equation
• Maxwells First Equation ( ):
When a dielectric is placed in a uniform electric field , its molecule get
polarized. Thus ,a dielectric in an electric field contains two type of
charges- free charge and bound charge . if and be the free and
bound charge densities respectively, at appoint in a small volume element
dv, then for such a medium, Gausss law may be expressed as
1/11/2017
Dr A K Mishra, Academic Coordinator,
JIT Jahangirabad
13
 D.orD 

div
 p
dvsdE
dvsdE
s
s
)Pdiv-(
1
.
thereforeon.polarizatielectricisPwhere,Pdiv-
densitychargeboundnowthe
space.freeofypermitivittheiswhere
..(1)..............................)(
1
.
v0
p
0
v
p
0
















14. Continued…………..
• Using Gauss divergence theorem on left hand side of the above equation,
we get
1/11/2017
Dr A K Mishra, Academic Coordinator,
JIT Jahangirabad
14
equation.requiredtheisthisD.
Ddivor0-Ddiv
havewefunction,arbitraryanfor,therefore
0dv)-D(divordVdvDdiv
.ent vectordisplacemaelectrictheisD)P(
dVdV)P(
dvdvPdivdvEdiv
dvdvPdivdvEdiv
dVPdiv
1
-dV
1
dVEdiv.
vv
0
vv
0
v v
0
v
v vv
0
v0v0






















 
 
 








Ebut
Ediv
or
sdE
s v

15. Derivation of Maxwell's Second Equation
• The net magnetic flux through any closed surface is always zero.
Using Gauss theorem
The above expression shows that monopole or an isolated pole
can not exist to serve as a source. this law is also known as Gauss law in
magnetostatics. where V is the volume enclosed by surface S.
Hence ,for an arbitrary surface div B = 0 or
1/11/2017
Dr A K Mishra, Academic Coordinator,
JIT Jahangirabad
15
.......(1)....................0.B
s
  sd
B


0dVBdiv
dVBdiv.B
v
vs






sd
0B. 

0B. 


16. Derivation of Maxwell's third Equation (faraday
law of electromagnetic induction)
• According to faraday law of electromagnetic induction,induced emf
around a closed circuit is equal to the negative time rate of change of
magnetic flux i.e.
if B is the magnetic field induction, then the magnetic flux linked with
the area ds
On combining the equation (1) and (2) we get
according to definition the induced emf is related to the corresponding
field as
1/11/2017
Dr A K Mishra, Academic Coordinator,
JIT Jahangirabad
16
)1....(....................
t
- B



e
)2....(....................sd.B
s


B
(3)..............................sd.B-
s


e
(4)..............................l.dE-
l


e

17. Continued………..
Therefore from (3) and (4) will give
1/11/2017
Dr A K Mishra, Academic Coordinator,
JIT Jahangirabad
17
t
B
-Exor
t
B
-ECurl
0
t
B
sdECurlfunction,arbitrarybanFor
0sd
t
B
sdECurl
sd
t
B
-sdECurl
havewe,Thus
sdECurl-ld.
getweside,handlefton thetheoremstokstheusingnow
sd
t
-ld.or
ds)B.(
t
-ld.
s
ss
sc
sc
sc












































E
B
E
E

18. Maxwells fourth equation
(modified amperes law)
• According to ampere law
Using stokes theorem on left hand side of the above expression, we get
1/11/2017
Dr A K Mishra, Academic Coordinator,
JIT Jahangirabad
18






s.dJl.dB
sdJIformulathesin
l.d
0
0





gu
IB
JdivHCurl
surface,arbitraryanFor0sd)J-(Curlor
sdJsd.HCurl
B
propertiesdielectricfromnowsdJsd.
B
s.dJs.dBCurl
1
sdJsdB
s
s
0
s
0
s0
s
0









 







H
Curl
Curl
s
s
s




19. Continued…………………
• Taking div on both side we get ,
This shows amperes law applicable for static charges, therefore Maxwell's
suggested that ampere law must be modified by adding a quantity having dimension as
that of current, produced due to polarization of charges. this physical quantity is called
displacement current (Jd).thus modified ampere law becomes
1/11/2017
Dr A K Mishra, Academic Coordinator,
JIT Jahangirabad
19
(static)constant
0
t
Hence
0
t
Jdiv
haveweequation,continutyfrom0JdivSince
)calculusvector(from0Hcurldivbut
JdivHCurldiv















20. Continued………
1/11/2017
Dr A K Mishra, Academic Coordinator,
JIT Jahangirabad
20
t
D
JHCurl
becomeslawAmperemodifie
t
D
or)(div
D)(div
t
divsinceDdiv
t
-Jdiv
div-Jdiv
divJdiv0
)0HCurl(divdivJdiv0
)(JdivHcurldiv
getweside,bothondivergencetakingJH
JJ
j
J
J
J
J
J
dd
d
d
d
d
d
d




















Therefore
t
D
div
but
But
Curl



21. Electromagnetic Energy (Pointing theorem)
• This is the analysis of transportation of energy from one place to
another due to propagation of electromagnetic waves.
Maxwell third and fourth equation in differential form are as follows
1/11/2017
Dr A K Mishra, Academic Coordinator,
JIT Jahangirabad
21
(4)....................
t
D
.EJ.E)Hx(Eand
.(3)..........
B
H-)Ex(Hgetwe
E,with(2)eqnandHwith(1)eqnofproductscalarTaking
)........(2....................
t
D
JHx
...(1)..............................
B
-Ex




















t
t

22. Continued…………………
• Subtracting eqn (5) from eqn (4)
1/11/2017
Dr A K Mishra, Academic Coordinator,
JIT Jahangirabad
22
J.E-
)E.(E
2
1)H.(H
2
1
-)HxE(.
J.E-
)(
2
1)(
2
1
-)HxE(.
J.E-
t
E)(
t
H)(
H-)HxE(.
Becomes
(6)equationtheso,EDandHBmedium,linearafor
......(6)..........J.E-
t
D
E
t
B
.H-)HxE(.
becomesequationaboveThe
)Hx(.E-)Ex(.H)HxE(.
identityvectortheusing
t
D
.E-J.E-
t
B
.H-)Hx(E-)Ex(H
EH
22














tt
tt
Now










































23. Continued……………….
• hence
1/11/2017
Dr A K Mishra, Academic Coordinator,
JIT Jahangirabad
23

 
  
























sv
v
s v
.....(7)...........ds)HxE(-dV)H.B.DE(
2
1
t
)J.E(
)J.E()H.(B
2
1
)D.(E
2
1
tt
-s)dHx(
getweside,handlefton thetheoremdivergencegausssin
)J.E()H.(B
2
1
)D.(E
2
1
t
-.dV)HxE(.
getweS,Surfaceabyboundedvvolumeaovergintegratin
J.E-)H.(B
2
1
)D.(E
2
1
t
-)HxE(.
J.E-
)D.(E
2
1
t
)B.(H
2
1
-)HxE(.
dV
dVdVE
gu
dVdV
t
v
vs
v






24. Continued…………
• Equation (7) is known as Pointing theorem. each term has its own physical
significance which is as follows:
• The term is the generalized statement of Joules law and
represent the total power dissipated in volume V.
• The first term on right hand side of the equation is the sum of energy
stored in electric field (E.D)and in magnetic field (B.H) or the total energy
stored in electromagnetic field. therefore this term represents the rate of
change in energy stored in volume V.
• The last term represents the law of conservation of energy, hence it
represents
• The rate at which the energy is carried out of volume V across its boundry
surface by electromagnetic waves.
1/11/2017
Dr A K Mishra, Academic Coordinator,
JIT Jahangirabad
24
dVJE
v
).(

25. Continued…………
• Thus the pointing theorem state that the work done on the
charge by an electromagnetic force is equal to the decrease in
energy stored in the field, less than the energy which flowed out
through the surface. it is also called the energy conservation law
in electrodynamics.
• The energy per unit time, per unit area transported by
electromagnetic field is called the pointing vector and is given by
1/11/2017
Dr A K Mishra, Academic Coordinator,
JIT Jahangirabad
25
)HxE(
1
HxE
0





Sor
S

26. Electromagnetic waves in free space
and its solution
• For free space or vacuum, Maxwell,s equations are as follows:
1/11/2017
Dr A K Mishra, Academic Coordinator,
JIT Jahangirabad
26
)
t
B
(-xExx
getwe(3),equationofcurlthe
)4..(..........
t
E
Bx
......(3)..........
t
B
-Ex
..(2)....................0B.
...(1)....................0E.
0o



















Taking


27. Continued………………..
• Using identity
1/11/2017
Dr A K Mishra, Academic Coordinator,
JIT Jahangirabad
27
.......(5)....................Eor
(4)equationusing
t
E.
(1)equationusing)Ex(
t
-E.-0
t
B
-xE).(-)E.(
getwe,C)B.A(-B)C.A()CxB(x
2
2
00
2
00
2
2
t
E
t
E
A


























28. Continued………………..
• Equation (5)is a wave equation for electric field in free space, similarly, for
magnetic field, we have
1/11/2017
Dr A K Mishra, Academic Coordinator,
JIT Jahangirabad
28










0
0
0
0
00
002
2
2
2
2
2
2
00
2
4
1
x
4
1
4x
4
1
v
11
or
1
space.freeinvectormagneticandelectricofnpropogatioof
velocitygives(7)equationwith(6)(5)orequationCompairing
)7.(....................
1
y
as,givenisvelocity v
awithgpropagatinwaveaofequationtheNow
)........(6..........B
v
v








v
B
B
t
t

29. Continued………………..
• Now,
1/11/2017
Dr A K Mishra, Academic Coordinator,
JIT Jahangirabad
29
light.ofvelocity
withspacefreeinpropogateswavesneticelectromaghence
light)of(velocitycm/sx3
x9x
1
x9
4
1
andm-
A
Wb
4
10
10
10
1010
8
9
7-
9
0
7-0



v
v




30. Depth of Penetration: (Skin Depth):
• It has been observed that an electromagnetic waves shows exponential
damping with distance due to various dissipative effect in the medium. In
conductors the rate of attenuation (loss of amplitude with distance) is very
high and the electromagnetic waves get almost attenuated after traversing
a quite distance.
Skin depth :
Describe the conducting behavior in electromagnetic field and in radio
communication. it is defined as the depth for which the strength of
electric field associated with the electromagnetic waves reduces to
times to the initial value.
1/11/2017
Dr A K Mishra, Academic Coordinator,
JIT Jahangirabad
30
e
1

31. Continued………………..
In terms of attenuation constant
1/11/2017
Dr A K Mishra, Academic Coordinator,
JIT Jahangirabad
31
0.368
1.0
E
Distance travelled 
X
The amplitude of electric field
of an electromagnetic waves
is decreased by a factor
therefore according to
definition of skin depth we
should have
e
ax

32. Continued………………
1/11/2017
Dr A K Mishra, Academic Coordinator,
JIT Jahangirabad
32
frequency.oftindependenisdepthskinthe,dielectricforThus,
medium.theofypermitivittheis,where
2
asgivenbemay
depthskintheinsulatorsordielectricgoodorconductorspoorFor
frequencyinincreasewithdecreasesdepthskinthus
f
1
f2
2
21
isdepthskintheTherefore,
ty.conductivitheisandmediumtheofindex
refractiveisfrequency,angulariswhere
2
haveweconductorsgooda
)1.(....................
constantnAttenuatio
1
depthskin.
1
xor1x
e
1
e
1-



























For
ei
e
x