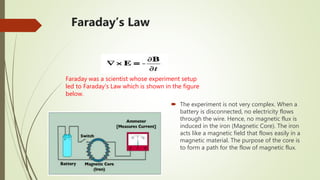
Maxwell's equations describe the relationship between electric and magnetic fields. Gauss' law states that the divergence of the electric flux density equals the electric charge density. Gauss' magnetism law states that the divergence of the magnetic flux density is always zero. Faraday's law describes how a changing magnetic field generates an electric field. Ampere's law shows the relationship between electric current and the surrounding magnetic field. Maxwell unified electricity, magnetism, and light through his equations, which can be written in differential or integral form and describe fields in free space or harmonically varying fields.

1. Department of Electrical & Electronic Engineering
Name: AL-AMIN
ID:16102904
Date: Sunday, September 23, 2018

2. 1.Definition & History of Maxwell’s equations:
Gauss Law
Gauss’ Magnetism Law
Faraday’s Law
Ampere’s Law
Maxwell’s equations in-
differential form
integral form
free space
Harmonically Varying fields

3. Maxwell’s equations
Maxwell's equations describe how electric
charges and electric currents create electric and
magnetic fields. Further, they describe how an electric
field can generate a magnetic field, and vice versa.

4. Gauss Law
 Gauss law describes the nature of
electric field around electric charges.
The law is expressed in terms of
electric charge density and electric
charge density.
 The inverted triangle is called as the
divergence operator.
 The equations hold good at any point
in space. When the electric charge
exists any somewhere, the divergence
of D at that particular point is
nonzero, else it is zero.

5. Gauss’ Magnetism Law
 You can see that both the equations
indicate the divergence of the field.
The top equation states that the
divergence of the Electric flux density
D equals the volume of electric
charge density.
 The second equation states the
divergence of the Magnetic Flux
Density (B) is null.

6. Faraday’s Law
Faraday was a scientist whose experiment setup
led to Faraday’s Law which is shown in the figure
below.
 The experiment is not very complex. When a
battery is disconnected, no electricity flows
through the wire. Hence, no magnetic flux is
induced in the iron (Magnetic Core). The iron
acts like a magnetic field that flows easily in a
magnetic material. The purpose of the core is
to form a path for the flow of magnetic flux.

7. Ampere’s Law
 The law shows the relationship between the
flow of electric current and the magnetic field
around it. Suppose the wire carries a current I,
the current produces a magnetic field that
surrounds the wire.

8. Differential form

10. Where Q is the total charge within the volume v.
Or, simply
Or, simply
Integral form:

11. or
and
or

12. Thus ,summarizing ,we have

13. In Free space:
Differential Form:

14. Integral form:

15. Harmonically Varying Field:

16. Also,
Or,