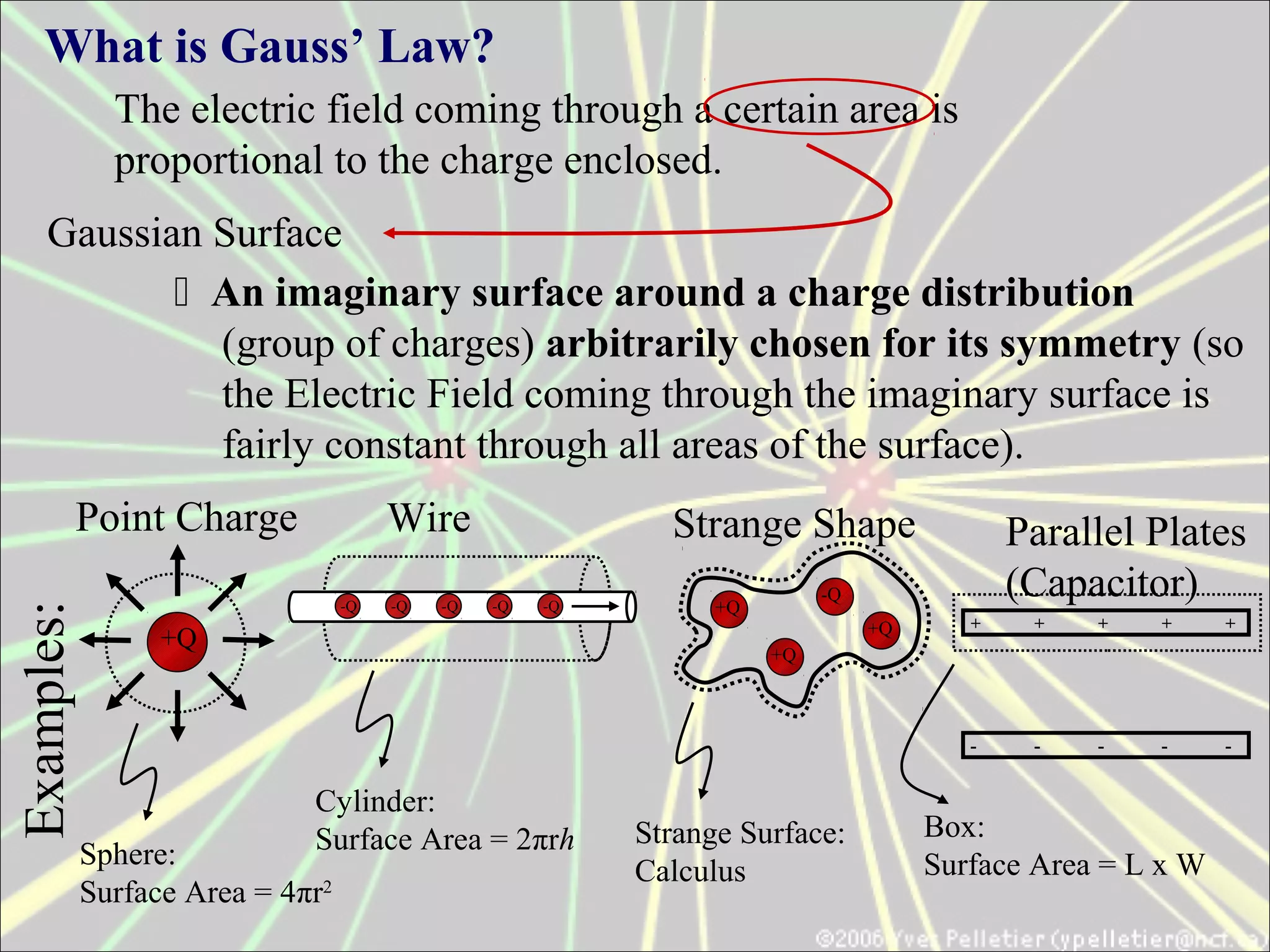
There are 4 pillars that make up the foundation of Electricity & Magnetism: 1) Gauss' Law (Electricity), which states that the electric field through a closed surface is proportional to the enclosed charge. 2) Gauss' Law (Magnetism), 3) Faraday's Law of Induction, and 4) Ampere's Law. Gauss' Law for electricity, proposed by Carl Friedrich Gauss, relates the total electric flux through a closed surface to the electric charge enclosed by the surface.

1. Electricity & Magnetism Maxwell’s
Equations
Faraday’s law of induction
Gauss’ Law (Magnetism)
Gauss’ Law (Electricity)
There are 4 pillars that
Ampere’s Law
make up the foundation
of Electricity &
Magnetism.
We’ll study each of
these in varying
degrees.

2. First Pillar: Gauss’ Law
Karl Fredrick Gauss (1777-1855)
He was a contemporary of Charles Coulomb (1736-1806)
Instead of finding the field from a single charge, Gauss found the field
from a bunch of charges (charge distribution).
Why is Gauss’ Law important?
Specific General
Coulomb’s Law finds a Gauss’ Law finds a field/charge
field/charge from point charges. from any charged object.
+Q
+Q -Q
+Q
+Q

3. What is Gauss’ Law?
The electric field coming through a certain area is
proportional to the charge enclosed.
Gaussian Surface
 An imaginary surface around a charge distribution
(group of charges) arbitrarily chosen for its symmetry (so
the Electric Field coming through the imaginary surface is
fairly constant through all areas of the surface).
Point Charge Wire Strange Shape Parallel Plates
-Q -Q -Q -Q -Q +Q
-Q (Capacitor)
Examples:
+Q + + + + +
+Q +Q
- - - - -
Cylinder:
Surface Area = 2πrh Strange Surface: Box:
Sphere: Surface Area = L x W
Calculus
Surface Area = 4πr2

4. What is Gauss’ Law?
2
The electric field coming through a certain area is
proportional to the charge enclosed. 3
2. Electric Fields
Quick reminders on Electric Field Lines
1. More field lines = stronger field.
2. Field lines always come out of the surface perpendicularly.
3. Out of +, into ‒
(show the direction a + charge will move)
3. Charge enclosed
The field is proportional to the charge inside the Gaussian Surface.
More Field Lines = Stronger Field = Stronger Charge Inside.

5. The electric field coming through a certain area is
Gauss’ Law: proportional to the charge enclosed.
∫EdA α Q
How do we make this an equation? – Add a constant!
∫EdA = cQ
c = 1/εo  remember this?!?
Permitivity Constant
εo = 8.85x10-12 Nm2/C  k = 1/4πεo = 8.99 x 109 Nm2/C2
Q
∫ EdA = ε o
How much field through a certain area
Rename this to be Electric Flux (ΦE)  how much field comes through a
certain area.

6. And finally…
Gauss’ Law Summary
The electric field coming through a certain area is
proportional to the charge enclosed.
Q
Φ E = ∫ EdA =
εo
ΦE = Electric Flux (Field through an Area)
E = Electric Field
A = Area
q = charge in object (inside Gaussian surface)
εo = permittivity constant (8.85x 10-12)

7. Sample Problem 1
A Van de Graaff machine with a radius of 0.25 m
has been charged up. What is the electric field
0.1 m away from the center of the sphere?
Hint: Where are all the charges? On the outside.
So how much charge is in the center? None.
0
Φ E = EA = =0
εo
Since all the charge is on the surface, it proves there is no field
inside a conducting surface!

8. Sample Problem 2
Find the electric field around a point charge,
Q.
Remember the area of a sphere (Gaussian
Q
Surface in this case) is 4πr2.
EA =
εo
E (4πr ) =
2 Q +Q
εo
Q 1
E= → don' t forget k =
4πε o r 2
4πε o
kQ What does this look like?
E= 2 Coulomb’s electric field for point charges!
r

9. Sample Problem 3
A solid sphere of radius R = 40 cm has a total positive
charge of 26 μC uniformly distributed throughout its
volume. Calculate the magnitude of the electric field at
the following distances from the center of the sphere.
(a) 0 cm (b) 30 cm (c) 60 cm
Inside sphere Q = 0 Still inside sphere
∴Q still = 0 Q
Φ E = EA =
εo
Q Q
Φ E = EA = Φ E = EA = Q
εo εo E (4πr ) =
2
εo
0 0
Φ E = EA = =0 Φ E = EA = =0 26 x10 −6
εo εo E (4π 0.6 2 ) =
8.85 x10 −12
E = 6.49 x105 N / C

10. Sample Problem 3
A solid sphere of radius R = 40 cm has a total positive
charge of 26 μC uniformly distributed throughout its
volume. Calculate the magnitude of the electric field at
the following distances from the center of the sphere.
(a) 0 cm (b) 30 cm (c) 60 cm
Inside sphere Q = 0 Still inside sphere
∴Q still = 0 Q
Φ E = EA =
εo
Q Q
Φ E = EA = Φ E = EA = Q
εo εo E (4πr ) =
2
εo
0 0
Φ E = EA = =0 Φ E = EA = =0 26 x10 −6
εo εo E (4π 0.6 2 ) =
8.85 x10 −12
E = 6.49 x105 N / C