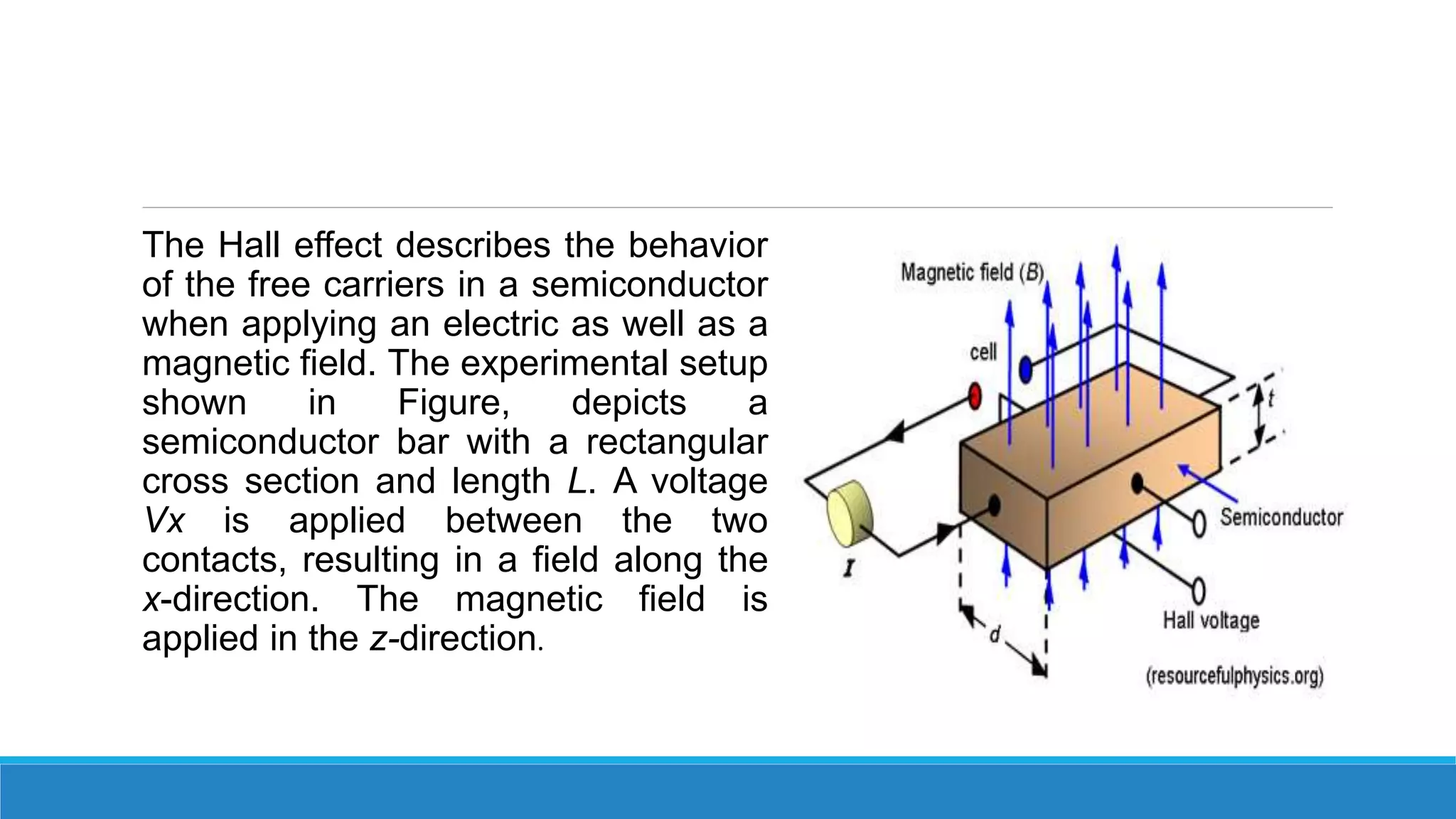
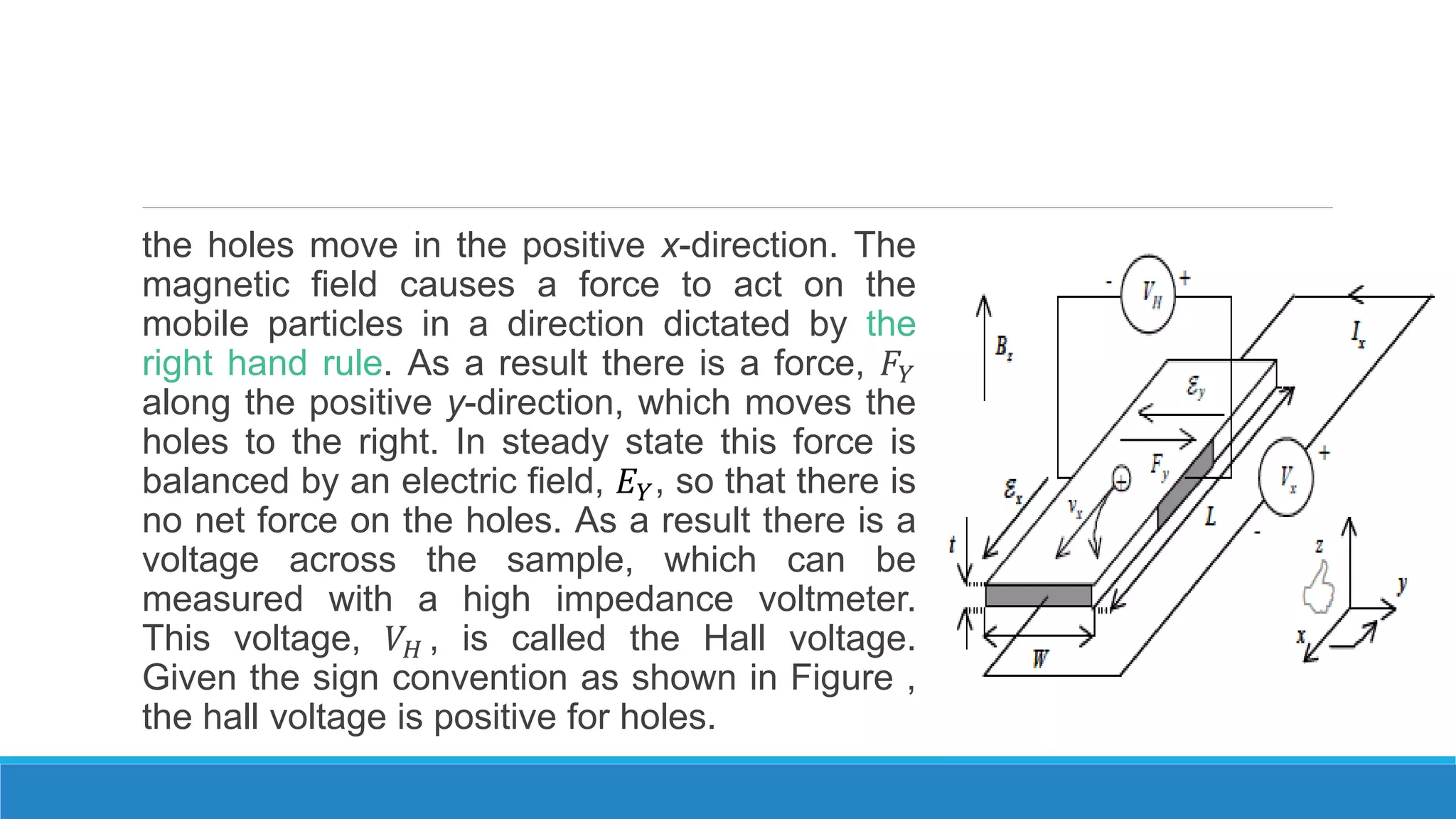
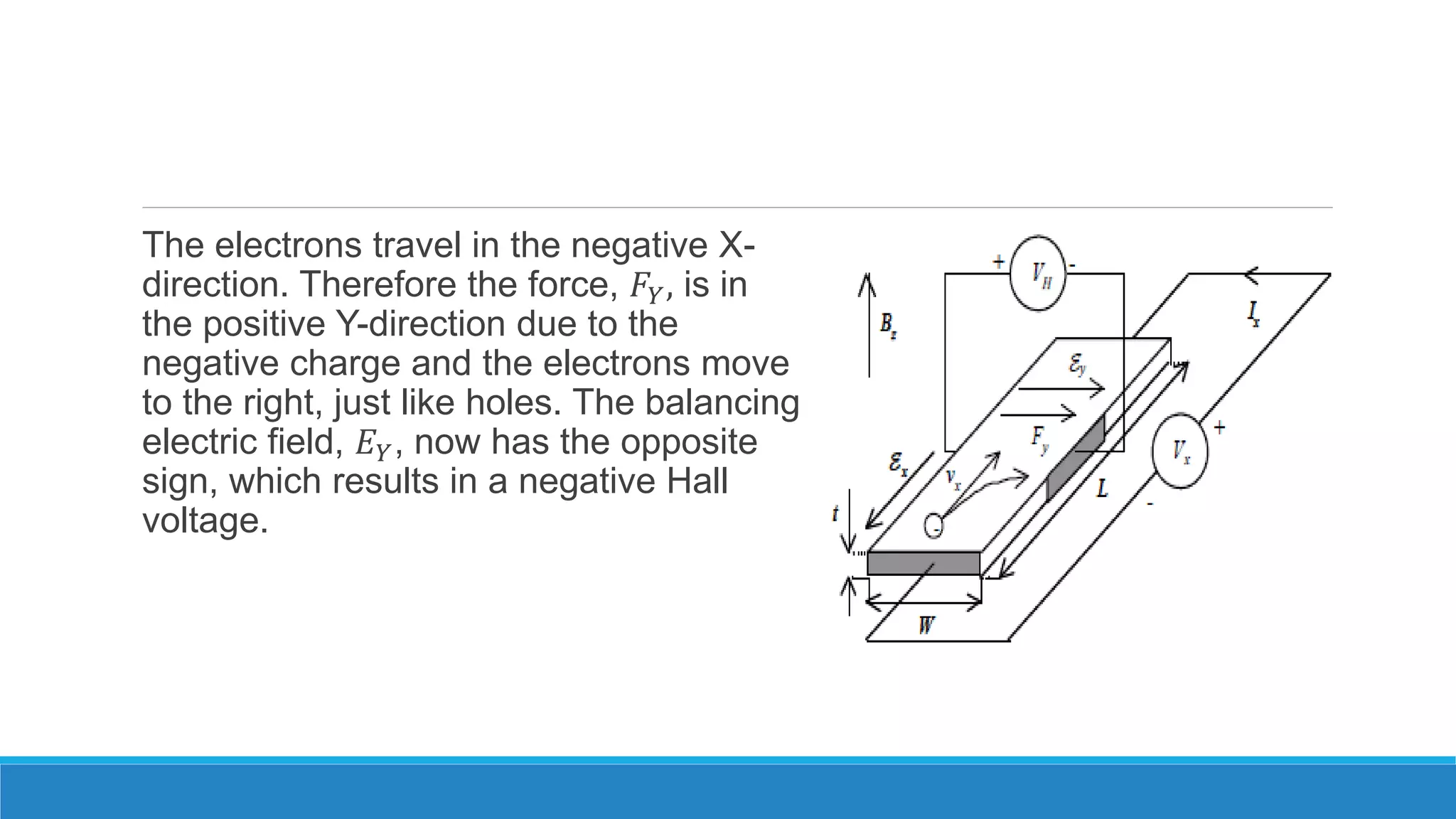
The Hall effect describes the behavior of charge carriers in a semiconductor when an electric and magnetic field are applied. When a current is passed through a semiconductor sample placed in a magnetic field perpendicular to the current, the Lorentz force causes charge carriers to deflect to the sides of the sample. This builds up a Hall voltage that can be measured. The Hall effect can be used to determine the type of semiconductor, calculate carrier concentration and mobility, and measure magnetic flux density.

1. Hall effect
BY :HEBA BAKRY

2. Introduction
The Hall effect describes the behavior of the free carriers in a
semiconductor when applying an electric as well as a magnetic field.
One important characterization tool in the measurement of the Hall
effect to measure mobilities and carrier concentrations in a given
semiconductor material. In this experiment, we will make such
measurements, observing the Hall effect for one semiconductor sample.
The temperature dependence of the Hall coefficient and resistivity will
allow us to distinguish between p-type and n-type samples, and to
calculate the electron and hole mobilities and concentrations.

3. Hall effect
Is a phenomenon that occurs when a conductor or semiconductor is
placed in the magnetic field and a voltage is applied through the material
perpendicular to the magnetic field. While this voltage induces current
flow along the electric field direction, the charge carriers also experience
a magnetic deflection from their path. This results a separation of positive
and negative carriers, and thus the generation of an electric field
perpendicular to the direction of current flow. Note that, at sufficient
temperature, the net current in a semiconductor is made up of
counteracting currents of p-type and n-type carriers

4. The Hall effect describes the behavior
of the free carriers in a semiconductor
when applying an electric as well as a
magnetic field. The experimental setup
shown in Figure, depicts a
semiconductor bar with a rectangular
cross section and length L. A voltage
Vx is applied between the two
contacts, resulting in a field along the
x-direction. The magnetic field is
applied in the z-direction.

5. the holes move in the positive x-direction. The
magnetic field causes a force to act on the
mobile particles in a direction dictated by the
right hand rule. As a result there is a force, 𝐹𝑌
along the positive y-direction, which moves the
holes to the right. In steady state this force is
balanced by an electric field, 𝐸 𝑌, so that there is
no net force on the holes. As a result there is a
voltage across the sample, which can be
measured with a high impedance voltmeter.
This voltage, 𝑉𝐻 , is called the Hall voltage.
Given the sign convention as shown in Figure ,
the hall voltage is positive for holes.

6. The electrons travel in the negative X-
direction. Therefore the force, 𝐹𝑌, is in
the positive Y-direction due to the
negative charge and the electrons move
to the right, just like holes. The balancing
electric field, 𝐸 𝑌, now has the opposite
sign, which results in a negative Hall
voltage.

7. Hall effect experiment
Consider a current-carrying conductor in the form of a rectangular strip is
placed in a magnetic field with the lines of force at right angles to the
current, a transverse e.m.f. – the so called Hall voltage – is set up across
the strip. This phenomenon is due to the Lorentz force: the charge
carriers which give rise to the current flow through the specimen are
deflected in the magnetic field B as a function of their sign and of their
velocity v:
𝐹𝐵 = 𝑞𝐵𝑉𝑑 …(1)
Where 𝑉𝑑 is Drift velocity which is the average velocity in the direction of
an applied electric field of the all conducting charge carriers in the sample

8. As more and more carriers are deflected, the accumulation of charge
produces a “Hall field” EH that exerts a force opposite to the Lorentz
force.
So the electric force:
𝐹𝐸 = 𝑞𝐸 …(2)
Equilibrium is reached when these two opposing forces are equal in
magnitude, which allows us to determine the drift speed (v)
𝑞𝐵𝑉𝑑 = 𝑞𝐸
∴ 𝑉𝑑 =
𝐸
𝐵
=
𝑉 𝐻
𝐵𝑑

9. but the current in the conductor is given by…
I=n e Vd A
so Vd=
𝑰
𝑨 𝒏𝒆
…(2)
From equation (1) & (2) we get that…
𝑩𝑰
𝑨𝒏𝒆
=
𝑽 𝑯
𝒅
…(3)
And it is customary to define the “Hall coefficient” (RH) in terms of the
measured quantities: 𝑹 𝑯 =
𝟏
𝒏𝒆

10. From equation (3) we get that…
𝑽 𝑯
𝑰
=
𝑩𝒅
𝑨𝒏𝒆
= 𝑹
As R is the resistance of the rectangular strip
But 𝑹 = 𝝆
𝒅
𝑨
∴ 𝝆 =
𝑩
𝒏𝒆
Where ρ is the resistivity
And 𝝈 =
𝒏𝒆
𝑩
Where σ is the conductivity
And from this equation we can Determine the mobility of the charge carriers which
given by
𝝁 =
𝝈
𝒏𝒆

11. Consider a semiconductor sample placed
in the magnetic field B that is in the z-
direction (refer to figure). Suppose we
pass a current I through that sample
perpendicular to the magnetic field, say in
the x-direction. Then the "free" electrons
and "holes" in the sample experience a
force given by the Lorentz equation,
(1)
Hall Effect Geometry

12. Applications of Hall effect
(1) Determination of N-type of semiconductor
For a N-type semiconductor, the Hall coefficient is negative
whereas for a P-type semiconductor, it is positive. Thus from the direction of the
Hall voltage developed, one can find out the type of semiconductor.
(2) Calculation of carrier concentration
Once Hall coefficient RH is measured, the carrier concentration
can be obtained,
HH eR
por
eR
n
1
)(
1


13. (3) Determination of mobility
We know that, conductivity,  = e q (or)
Thus by measuring `’ and RH, ’ can be calculated.
(4) Measurement of magnetic flux density.
Using a semiconductor sample of known `RH’, the magnetic flux density can be
deduced from,
Hp
p
n R
pe
.

 
IR
tV
B
H
H
