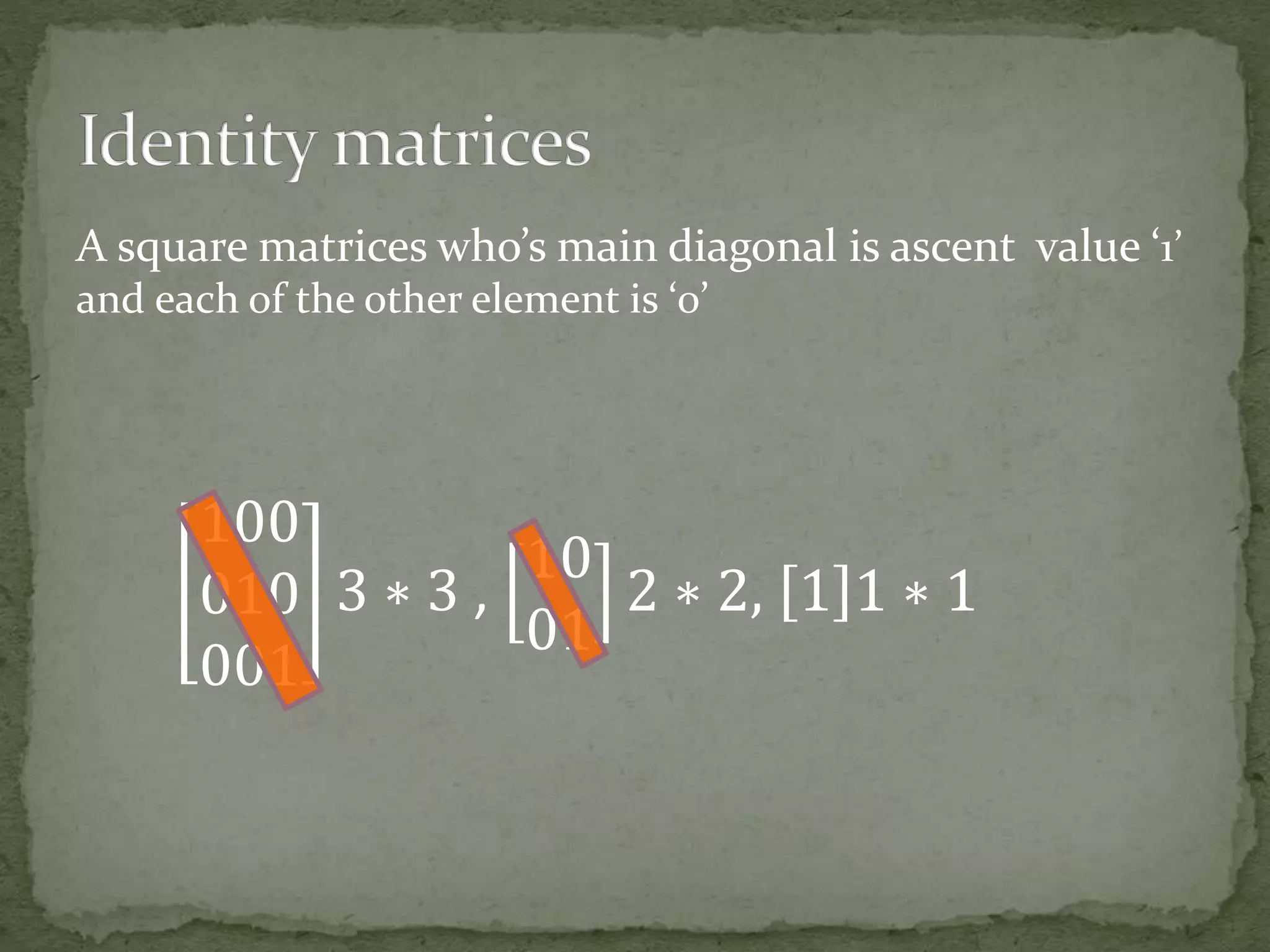This document discusses matrices and their uses. It defines what a matrix is and provides examples of different types of matrices like row matrices, column matrices, null matrices, identity matrices, diagonal matrices, triangular matrices, and transpose matrices. It then discusses some applications of matrices like in cryptography for encrypting messages, in electrical circuits, quantum mechanics, optics, robotics, automation, economics, and more. Matrices are useful for tasks like plotting graphs, scientific studies, page ranking algorithms, image projection, representing real world data, and calculating gross domestic products.

1. Md: Mahmudle Hassan
Department of Civil Eng.
At Daffodil International University
https://www.facebook.com/MHMMEHEDI12
Website: https://needtune.blogspot.com

2. Matrices
 A rectangular arrangement of numbers in rows and
columns.
 It is the Combination of linear equation.
 It is Represented by these symbols:
[], ||,()

3. EXAMPLE






197
324
)a










29
37
05
)b
 381) c 









512
348
1097
)d
row
column column
row
row
column column
row

4. DIMENSIONS OF THE MATRIX
Row (m)






234
012
Column(n)
A matrix with m rows and n columns is called a matrix with dimensions m x n
(# no. of row) x ( # no. of
column)
This is a 2 X 3 matrix
DIMENSIONS OF THE
MATRIX :

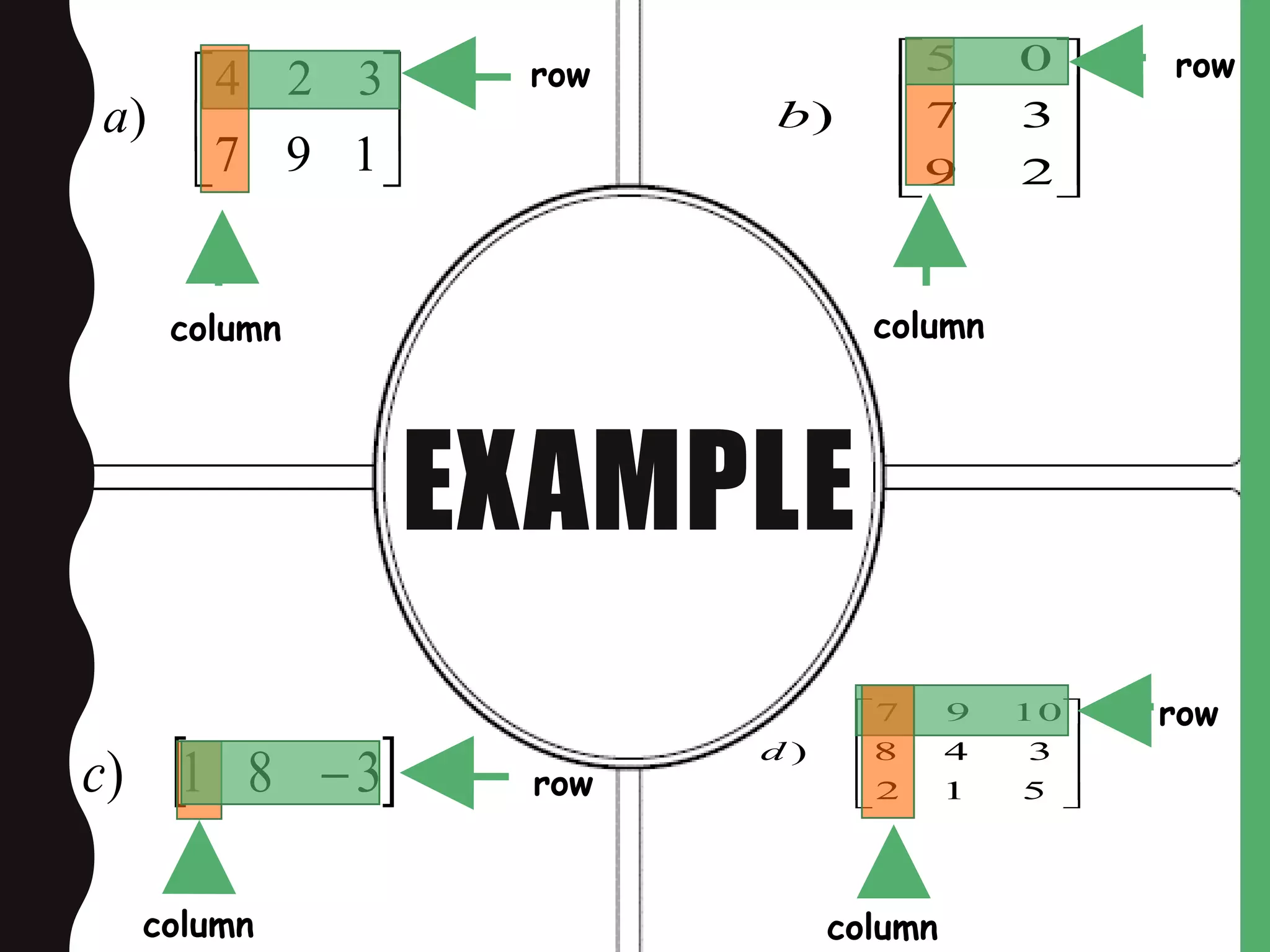
5. Types of Matrices
1. Row matrices – A matrices which has only one row
called row matrices e.g.-
[123]1*3
2. Column matrices – A matrices which has only one column
is called column matrices e.g. –

6. Null matrix is a matrix with all its entries being zero.

7. 123
456
789
3 ∗ 3
No of rows = No of column

8. A square matrices who’s main diagonal is ascent value ‘1’
and each of the other element is ‘0’
100
010
001
3 ∗ 3 ,
10
01
2 ∗ 2, 1 1 ∗ 1

9. A square matrices all of who’s element expect those in
the leading diagonal are ‘0’

10. A diagonal matrices in which all the elements of main
diagonal is same called scalar matrices.
3*3

11. There are two types triangular matrices ---
1.Upper triangular: All the below elements are ‘0’.
2.Lower triangular: All the above elements are ‘0’
123
045
006
3 ∗ 3
100
230
456
3 ∗ 3

12.  A matrices obtained by inter changing the rows and
columns of a matrices.
 It is denoted by A’ , AT
A⇒
123
456
789
3 ∗ 3 AT
⇒
147
258
369
3 ∗ 3

13.  Cryptography is the process of encrypting data so that
third party can’t read it and privacy can be maintained.
 It was started with the TV cable industries where even
people who were not the customer could watch the TV
programs

14.  Videocipher encryption system was invented which
would convert signals into digital form i.e. encrypt it,
and the data were send over the satellite.

15.  Since we are using a 3 by 3 matrix, we break the enumerated message
above into a sequence of 3 by 1 vectors:
 Note that it was necessary to add a space at the end of the message to
complete the last vector.
 We encode the message by multiplying each of the above vectors by the
encoding matrix.
 We represent above vectors as columns of a matrix and perform its
matrix multiplication with the encoding matrix






































































27
5
20
1
9
20
15
7
5
14
27
15
20
27
5
18
1
16
5
18
16



















 
271151420185
5972727118
202051551616
434
110
433

17.  matrices are used for taking seismic surveys.
 They are used for plotting graphs, statistics and also to
do scientific studies in almost different fields.

18.  matrices are applied in the study of electrical circuits,
quantum mechanics and optics.
 In the calculation of battery power outputs, resistor
conversion of electrical energy into another useful
energy, these matrices play a major role in
calculations.
 Especially in solving the problems using Kirchoff’s
laws of voltage and current, the matrices are essential.

19.  First, write a numerical value for each letter i.e. A=1,
B=2, and Z=26, and space=27.
 The data should be placed in matrix form i.e. in 2x1 or
3x1 matrix form.

20.  The data should be multiplied by given encoding
matrix.
 Then, write the answer (value after multiplying) in
linear form. How to encrypt data? Encryption Process

21.  matrices play a vital role in the projection of three
dimensional image into a two dimensional screen,
creating the realistic seeming motions.
 Stochastic matrices and Eigen vector solvers are used
in the page rank algorithms which are used in the
ranking of web pages in Google search.

22.  The matrix calculus is used in the generalization of
analytical notions like exponentials and derivatives to
their higher dimensions.
 One of the most important usages of matrices in
computer side applications are encryption of message
codes.
 Matrices and their inverse matrices are used for a
programmer for coding or encrypting a message.

23.  Matrices are used in representing the real world data’s like the traits of people’s
population, habits, etc.
 They are best representation methods for plotting the common survey things.

 • Matrices are used in calculating the gross domestic products in economics which
eventually helps in calculating the goods production efficiently.

 • Matrices are used in many organizations such as for scientists for recording the data
for their experiments.

 • In robotics and automation, matrices are the base elements for the robot movements.
 The movements of the robots are programmed with the calculation of matrices’ rows and
columns.
 The inputs for controlling robots are given based on the calculations from matrices.