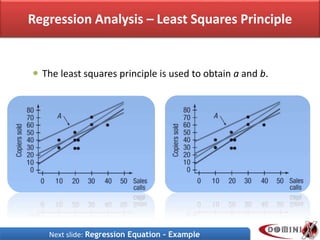
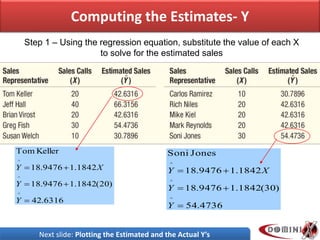
The document discusses linear regression analysis. It defines a regression equation as an equation that expresses the linear relationship between two variables. It explains that regression analysis uses the independent variable (X) to estimate the dependent variable (Y), and that the relationship is determined using the least squares method to minimize the difference between predicted and actual Y values. It provides an example of finding the regression equation relating number of sales calls to copiers sold.

2. Regression Equation
Next slide: Linear Regression Model
An equation that expresses the linear
relationship between two variables.

3. Linear Regression Model
Next slide: Computing the Slope of the Line and the Y-intercept

4. Computing the Slope of the Line and the Y-intercept
Next slide: Regression Analysis

5. In regression analysis we use the independent variable (X) to
estimate the dependent variable (Y).
• The relationship between the variables is linear.
• Both variables must be at least interval scale.
• The least squares criterion is used to determine the equation.
LEAST SQUARES PRINCIPLE Determining a regression equation by
minimizing the sum of the squares of the vertical distances between the
actual Y values and the predicted values of Y.
Regression Analysis
Next slide: Regression Analysis – Least Squares Principle

6. Regression Analysis – Least Squares Principle
 The least squares principle is used to obtain a and b.
Next slide: Regression Equation - Example

7. Recall the example involving
Copier Sales of America. The sales
manager gathered information on
the number of sales calls made
and the number of copiers sold for
a random sample of 10 sales
representatives. Use the least
squares method to determine a
linear equation to express the
relationship between the two
variables.
What is the expected number of
copiers sold by a representative
who made 20 calls?
Regression Equation - Example
Next slide: Finding the Regression Equation - Example

8. Finding the Regression Equation - Example
Next slide: Finding the Regression Equation - Example

9. Finding the Regression Equation - Example
Next slide: Finding the Regression Equation - Example

10. Finding the Regression Equation - Example
6316.42
)20(1842.19476.18
1842.19476.18
:isequationregressionThe
^
^
^
^




Y
Y
XY
bXaY
Next slide: Interpretation of ‘a’ and ‘b’

11. Interpretation of ‘a’ and ‘b’
Next slide: Computing the Estimates- Y
•‘b’ means, for each additional sales call made the sales
representative can expect to increase the number of copiers
sold by 1.1842.
•The ‘a’ value of 18.9476 is the point where the equation
crosses the y-axis. i.e. if no sales call made, the sale would be
18.9476.

12. Step 1 – Using the regression equation, substitute the value of each X
to solve for the estimated sales
6316.42
)20(1842.19476.18
1842.19476.18
KellerTom
^
^
^



Y
Y
XY
4736.54
)30(1842.19476.18
1842.19476.18
JonesSoni
^
^
^



Y
Y
XY
Computing the Estimates- Y
Next slide: Plotting the Estimated and the Actual Y’s

13. Plotting the Estimated and the Actual Y’s
Next slide: The Standard Error of Estimate

14. • The standard error of estimate measures the scatter, or
dispersion, of the observed values around the line of
regression
• Formulas used to compute the standard error:
2
2
.



n
XYbYaY
s xy
2
)( 2
^
.



n
YY
s xy
The Standard Error of Estimate
Next slide: Example

15. Recall the example
involving Copier Sales of
America. The sales manager
determined the least
squares regression
equation is given below.
Determine the standard
error of estimate as a
measure of how well the
values fit the regression
line.
XY 1842.19476.18
^

901.9
210
211.784
2
)( 2
^
.






n
YY
s xy
Example
Next slide: Excel

16. Excel
Next slide: Confidence Interval and Prediction Interval Estimates of Y

17. •A confidence interval reports the mean value of Y for a given X.
•A prediction interval reports the range of values of Y for a particular value
of X.
Confidence Interval and Prediction Interval
Estimates of Y
Next slide: Confidence Interval Estimate - Example

18. Confidence Interval Estimate - Example
We return to the Copier Sales of America illustration.
Determine a 95 percent confidence interval for all
sales representatives who make 25 calls.
Next slide: Confidence Interval Estimate - Example

19. Confidence Interval Estimate - Example
Step 1 – Compute the point estimate of Y
In other words, determine the number of copiers we expect a sales representative
to sell if he or she makes 25 calls.
5526.48
)25(1842.19476.18
1842.19476.18
:isequationregressionThe
^
^
^



Y
Y
XY
Next slide: Confidence Interval Estimate - Example

20. Confidence Interval Estimate - Example
Step 2 – Find the value of t
 To find the t value, we need to first know the number of
degrees of freedom. In this case the degrees of freedom is
n - 2 = 10 – 2 = 8.
 We set the confidence level at 95 percent. To find the
value of t, move down the left-hand column of Appendix
B.2 to 8 degrees of freedom, then move across to the
column with the 95 percent level of confidence.
 The value of t is 2.306.
Next slide: Confidence Interval Estimate - Example

21. Confidence Interval Estimate - Example
 2
XX 
  
2
XXStep 3 – Compute and 2
XX 
Next slide: Confidence Interval Estimate - Example

22. Confidence Interval Estimate - Example
Step 4 – Use the formula above by substituting the numbers computed
in previous slides
Thus, the 95 percent confidence interval for the average sales of
all sales representatives who make 25 calls is from 40.9170 up to
56.1882 copiers.
Next slide: Prediction Interval Estimate - Example

23. Prediction Interval Estimate - Example
We return to the Copier Sales of America
illustration. Determine a 95 percent
prediction interval for Sheila Baker, a West
Coast sales representative who made 25
calls.
Next slide: Prediction Interval Estimate - Example

24. Prediction Interval Estimate - Example
Step 1 – Compute the point estimate of Y
In other words, determine the number of copiers we expect a sales
representative to sell if he or she makes 25 calls.
5526.48
)25(1842.19476.18
1842.19476.18
:isequationregressionThe
^
^
^



Y
Y
XY
Next slide: Prediction Interval Estimate - Example

25. Step 2 – Using the information computed earlier
in the confidence interval estimation example,
use the formula above.
If Sheila Baker makes 25 sales calls, the number of
copiers she will sell will be between about 24 and 73
copiers.
Prediction Interval Estimate - Example
Next slide: Real Life Applications

26. Next slide: Calculating Values at Housing Business

27. Example 1: Calculating Values at Housing Business
Next slide: Calculating Values at Housing Business
Sizes and Prices of Eighteen Houses
X= Size Y=Price X= Size Y= Price
1.8 32 2.3 44
1.0 24 1.4 27
1.7 27 3.3 50
1.2 25 2.2 37
2.8 47 1.5 28
1.7 30 1.1 20
2.5 43 2.0 38
3.6 52 2.6 45

28. Calculating Values at Housing Business
Next slide: Relation between age and income
Here,
Y = a + bx
Price = 9.253 + 12.873(Size)
X= Size
Y= Price

29. Example 2: Relation between age and income
Next slide: Relation between age and income

30. Relation between age and income
Next slide: Thank You
Here,
Y = a + bx
Income = 22.88 - 0.05834 (Age)
X= Age
Y= Income