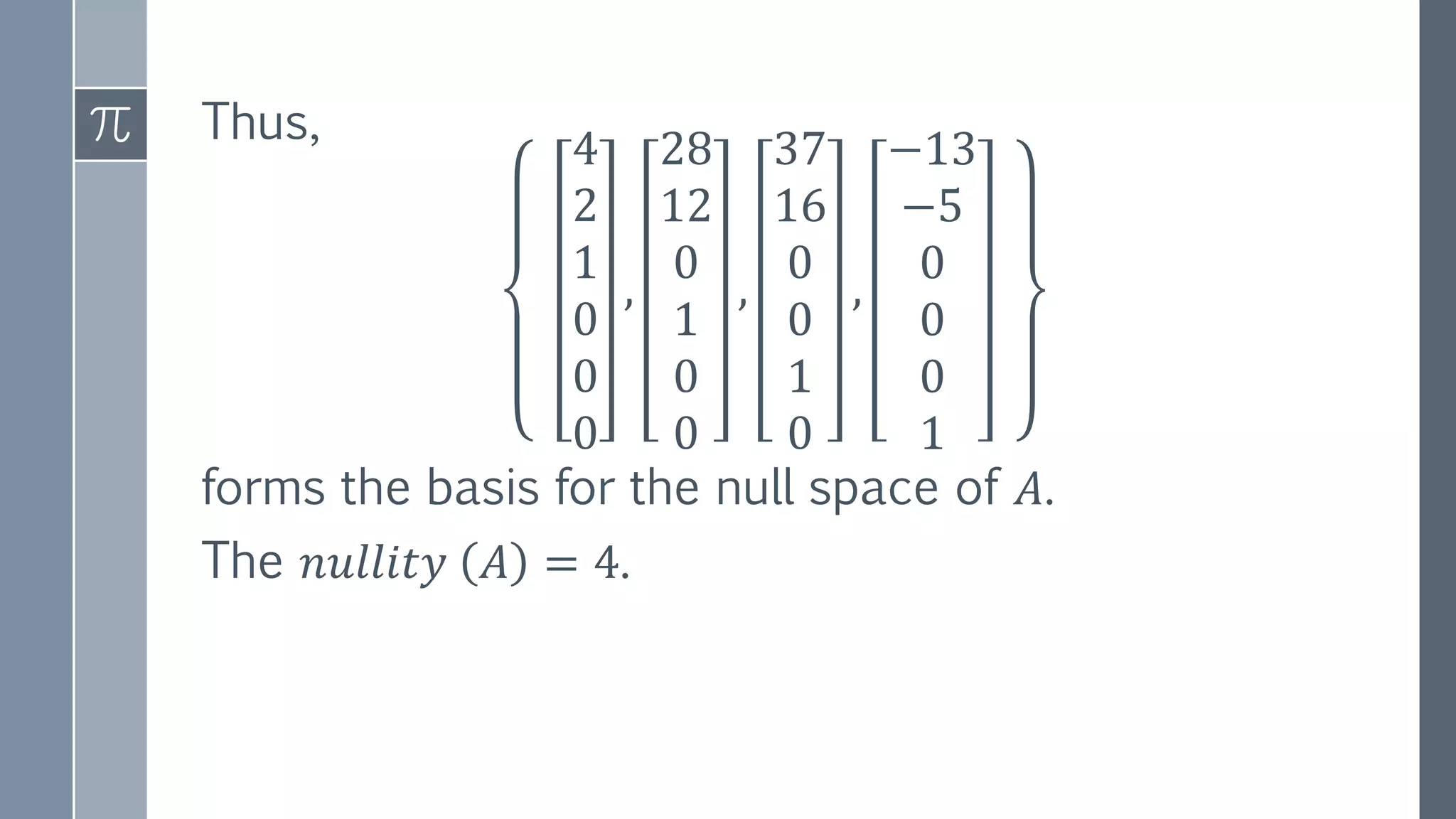
The document discusses rank and nullity of matrices, and the fundamental matrix spaces. It defines rank as the maximum number of linearly independent rows or columns. The row and column ranks of a matrix are equal, and represent the dimension of the row and column spaces. Nullity is defined as the dimension of the null space. Examples are provided to demonstrate calculating the rank and nullity of matrices by finding their reduced row echelon forms. The rank is the number of pivot columns, and the nullity is the number of free variables.

1. Rank, Nullity, and
Fundamental Matrix
Spaces
Math 209 – Linear Algebra
FROILAN R. DOBLON
Discussant

2. Objectives
At the end of the discussion, we will be able
to:
1. Define Rank and Nullity of a Matrix;
2. Describe the Fundamental Matrix
Spaces; and
3. Solve for the Rank and Nullity of a
Matrix.

3. Rank of a Matrix

4. Rank of a Matrix
› The concept of the rank of a matrix plays an
important role in the application of matrices to
linear problems. It helps us to find the consistency
of a system of simultaneous linear equations.
Theorem
If 𝐴𝑥 = 𝑏 is a consistent linear system of
𝑚 equations in 𝑛 unknowns, and if 𝐴 has
rank 𝑟, then the general solution of the
system contains 𝑛 – 𝑟 parameters.

5. Rank of a Matrix
› With each matrix, we can associate a non-negative
integer called its RANK.

6. Row Rank and Column Rank of a Matrix
Let 𝐴 be an 𝑚 𝑥 𝑛 matrix.
› The maximum number of linearly independent
rows (columns) in a matrix 𝐴 is called the row
(column) rank of A.
› The dimension of the row (column) space of 𝐴 is
called the row (column) rank of A.

7. Definition of Row (Column) Rank
Rank is the maximum number of independent rows
(columns).
𝐴 =
1 2
2 4
independent
dependent
Row Rank = 1.

8. Definition of Row (Column) Rank
𝐴 =
1 2
2 4
independent
dependent
Column Rank = 1.

9. What If…
𝐴 =
1 −2 0
3 2 8
2 3 7
−1 2 0
3 −4
1 4
2 3
4 −3

10. Definition of Row (Column) Rank
Rank is the dimension of the row (column) space of
𝐴.
Dimension of a Matrix
If 𝐴 is a subspace of 𝑅𝑛
, then the number of
vectors in a basis for 𝐴 is called the
dimension of 𝐴, denoted by dim(𝐴).

11. Example 1 (Row Rank)
Find a basis for the row space of the matrix 𝐴 .
Then, compute the row rank of 𝐴.
𝐴 =
1 −2 0
3 2 8
2 3 7
−1 2 0
3 −4
1 4
2 3
4 −3

12. Solution:
𝐴 =
1 −2 0
3 2 8
2 3 7
−1 2 0
3 −4
1 4
2 3
4 −3
Expressed in a linear combination:
𝑎1 1 −2 0 3 −4 + 𝑎2 3 2 8 1 4
+ 𝑎3 2 3 7 2 3 + 𝑎4 −1 2 0 4 −3
= 0 0 0 0 0

13. Solution:
𝑎1 1 −2 0 3 −4 + 𝑎2 3 2 8 1 4
+ 𝑎3 2 3 7 2 3 + 𝑎4 −1 2 0 4 −3
= 0 0 0 0 0
Augmented Matrix:
1 3 2
−2 2 3
0 8 7
3 1 2
−4 4 3
−1
2
0
4
3
0
0
0
0
0
= 𝐴𝑇
𝑶

14. Solution:
Transform to Reduced Row Echelon Form
1 3 2
−2 2 3
0 8 7
3 1 2
−4 4 3
−1
2
0
4
3
0
0
0
0
0
⇒
1 3 2
0 8 7
0 8 7
0 −8 −4
0 16 11
−1
0
0
7
−7
0
0
0
0
0
⇒
1 3 2
0 1 7/8
0 0 0
0 0 3
0 0 −3
−1
0
0
7
−7
0
0
0
0
0
⇒
1 3 2
0 1 7/8
0 0 3
0 0 0
0 0 −3
−1
0
7
0
−7
0
0
0
0
0
⇒
1 3 2
0 1 7/8
0 0 1
0 0 0
0 0 0
−1
0
7/3
0
0
0
0
0
0
0
⇒
1 0 0
0 1 0
0 0 1
0 0 0
0 0 0
11/24
−49/24
7/3
0
0
0
0
0
0
0

15. Solution:
Reduced Row Echelon Form:
𝐵 =
1 0 0
0 1 0
0 0 1
0 0 0
0 0 0
11/24
−49/24
7/3
0
0
0
0
0
0
0

16. Solution:
Since the leading 1’s occur in columns 1, 2, and 3,
we conclude that the first three rows of A form a
basis for the row space of A. That is,
{ 1 − 2 0 3 − 4 , 3 2 8 1 4 , 2 3 7 2 3 }
is a basis for the row space of A.
The row rank of A is 3.

17. Example 2 (Column Rank)
Find a basis for column space of the matrix 𝐴 .
Then, compute the column rank of 𝐴.
𝐴 =
1 −2 0
3 2 8
2 3 7
−1 2 0
3 −4
1 4
2 3
4 −3

18. Solution:
𝐴 =
1 −2 0
3 2 8
2 3 7
−1 2 0
3 −4
1 4
2 3
4 −3
Expressed in a linear combination
𝑎1
1
3
2
−1
+ 𝑎2
−2
2
3
2
+ 𝑎3
0
8
7
0
+ 𝑎4
3
1
2
4
+ 𝑎5
−4
4
3
−3
=
0
0
0
0

19. Solution:
𝑎1
1
3
2
−1
+ 𝑎2
−2
2
3
2
+ 𝑎3
0
8
7
0
+ 𝑎4
3
1
2
4
+ 𝑎5
−4
4
3
−3
=
0
0
0
0
Augmented Matrix:
1 −2 0
3 2 8
2 3 7
−1 2 0
3 −4
1 4
2 3
4 −3
0
0
0
0
= 𝐴 𝑶

20. Solution:
Transform to Reduced Row Echelon Form
1 −2 0
3 2 8
2 3 7
−1 2 0
3 −4
1 4
2 3
4 −3
0
0
0
0
⇒
1 −2 0
0 8 8
0 7 7
0 0 0
3 −4
−8 16
−4 11
7 −7
0
0
0
0
⇒
1 −2 0
0 1 1
0 0 0
0 0 0
3 −4
−1 2
3 −3
7 −7
0
0
0
0
⇒
1 −2 0
0 1 1
0 0 0
0 0 0
3 −4
−1 2
1 −1
0 0
0
0
0
0
⇒
1 0 2
0 1 1
0 0 0
0 0 0
1 0
−1 2
1 −1
0 0
0
0
0
0
⇒
1 0 2
0 1 1
0 0 0
0 0 0
0 1
0 1
1 −1
0 0
0
0
0
0

21. Solution:
Reduced Row Echelon Form:
𝐵 =
1 0 2
0 1 1
0 0 0
0 0 0
0 1
0 1
1 −1
0 0
0
0
0
0

22. Solution:
Since the leading 1’s occur in columns 1, 2, and 4,
we conclude that the first, second, and fourth
columns of A form a basis for the column space of
A. That is,
1
3
2
−1
,
−2
2
3
2
,
3
1
2
4
is a basis for the column space of A.
The column rank of A is 3.

23. Figure this out!
Given the matrix 𝐴:
𝐴 =
1 −2 0
3 2 8
2 3 7
−1 2 0
3 −4
1 4
2 3
4 −3
The row rank of 𝐴 is 3 and the column rank of 𝐴 is
3.
𝑟𝑜𝑤 𝑟𝑎𝑛𝑘 𝑜𝑓 𝐴 = 𝑐𝑜𝑙𝑢𝑚𝑛 𝑟𝑎𝑛𝑘 𝑜𝑓 𝐴.

24. Rank of a Matrix
𝑇ℎ𝑒 𝑟𝑜𝑤 𝑟𝑎𝑛𝑘 𝑎𝑛𝑑 𝑐𝑜𝑙𝑢𝑚𝑛 𝑟𝑎𝑛𝑘 𝑜𝑓 𝑎𝑛
𝑚 𝑥 𝑛 𝑚𝑎𝑡𝑟𝑖𝑥 𝐴 = 𝑎𝑖𝑗 𝑎𝑟𝑒 𝑒𝑞𝑢𝑎𝑙.
Since the row and column ranks of a matrix are
equal, we now merely refer to the rank of a matrix,
or 𝒓𝒂𝒏𝒌 (𝑨).

25. Rank of a Matrix
› The common dimension of the row and column
space of a matrix A is called the rank of A and is
denoted by 𝑟𝑎𝑛𝑘(𝐴);
› The rank of 𝐴 is the number of pivots or leading
coefficients in the echelon form. In fact, the pivot
columns (i.e., the columns with pivots in them) are
linearly independent.

26. Example 3:
Find the rank of Matrix A.
𝐴 =
1 2 3
4 5 6
7 8 9
.
Solution:
1 2 3
4 5 6
7 8 9
0
0
0
⇒
1 2 3
0 −3 −6
0 −6 −12
0
0
0
⇒
1 0 −1
0 1 2
0 0 0
0
0
0
∴ 𝒓𝒂𝒏𝒌 𝑨 = 𝟐

27. Nullity of a Matrix

28. Nullity of a Matrix
› The dimension of the null space of 𝐴 is called the
nullity of A and is denoted by 𝑛𝑢𝑙𝑙𝑖𝑡𝑦 (𝐴).
𝑛𝑢𝑙𝑙𝑖𝑡𝑦 𝐴 = dim(𝑁 𝐴 )
› It is easier to find the nullity than to find the null
space. This is because the number of free
variables (in the solved equations) equals the
nullity of A.

29. Basic (Leading) and Free Variables
› A variable is a basic variable if it corresponds to a pivot
column. Otherwise, the variable is known as
a free variable. In order to determine which variables
are basic and which are free, it is necessary to row
reduce the augmented matrix to echelon form.

30. Basic (Leading) and Free Variables
› Example:
𝑥1 + 2𝑥2 − 𝑥3 = 4
2𝑥1 − 4𝑥2 = 5
Augmented Matrix:
1 2 −1
2 −4 0
4
5
1 2 −1
0 −8 2
4
−3
1 2 −1
0 1 −1/4
4
3/8
1 0 −1/2
0 1 −1/4
13/4
3/8
𝒙𝟏 𝒙𝟐 𝒙𝟑
Pivot Columns
(because of pivot elements)
Basic (Leading) Variables: 𝑥1, 𝑥2

31. Basic (Leading) and Free Variables
› Example:
𝑥1 + 2𝑥2 − 𝑥3 = 4
2𝑥1 − 4𝑥2 = 5
Augmented Matrix:
1 2 −1
2 −4 0
4
5
1 2 −1
0 −8 2
4
−3
1 2 −1
0 1 −1/4
4
3/8
1 0 −1/2
0 1 −1/4
13/4
3/8
𝒙𝟏 𝒙𝟐 𝒙𝟑
Non-Pivot Column
Free Variables: 𝑥3

32. Example 4:
Using Matrix A in Example 3. Find the 𝑛𝑢𝑙𝑙𝑖𝑡𝑦 (𝐴).
𝐴 =
1 2 3
4 5 6
7 8 9
.
Solution:
1 2 3
4 5 6
7 8 9
0
0
0
⇒
1 2 3
0 −3 −6
0 −6 −12
0
0
0
⇒
1 0 −1
0 1 2
0 0 0
0
0
0
∴ 𝒏𝒖𝒍𝒍𝒊𝒕𝒚 𝑨 = 𝟏

33. Example 5
› Find a basis for the null space of 𝐴. Then,
determine the nullity of 𝐴, 𝑛𝑢𝑙𝑙𝑖𝑡𝑦 (𝐴).
𝐴 =
−1 2 0
3 −7 2
2 −5 2
4 −9 2
4 5 −3
0 1 4
4 6 1
−4 −4 7

34. Solution
› The reduced row-echelon form of A is
1 0 −4
0 1 −2
0 0 0
0 0 0
−28 −37 13
−12 −16 5
0 0 0
0 0 0
0
0
0
0

35. Solution
1 0 −4
0 1 −2
0 0 0
0 0 0
−28 −37 13
−12 −16 5
0 0 0
0 0 0
0
0
0
0
The corresponding system of equations will be
𝑥1 − 4𝑥3 − 28𝑥4 − 37𝑥5 + 13𝑥6 = 0
𝑥2 − 2𝑥3 − 12𝑥4 − 16𝑥5 + 5𝑥6 = 0.

36. 𝑥1 − 4𝑥3 − 28𝑥4 − 37𝑥5 + 13𝑥6 = 0
𝑥2 − 2𝑥3 − 12𝑥4 − 16𝑥5 + 5𝑥6 = 0.
There are four free variables; It follows that the general
solution of the system is
𝑥3 = 𝑟; 𝑥4 = 𝑠; 𝑥5 = 𝑡; 𝑥6 = 𝑢
𝑥1 = 4𝑟 + 28𝑠 + 37𝑡 − 13𝑢;
𝑥2 = 2𝑟 + 12𝑠 + 16𝑡 − 5𝑢;
Or 𝑥1
𝑥2
𝑥3
𝑥4
𝑥5
𝑥6
= r
4
2
1
0
0
0
+ s
28
12
0
1
0
0
+ t
37
16
0
0
1
0
+ 𝑢
−13
−5
0
0
0
1

37. Thus,
4
2
1
0
0
0
,
28
12
0
1
0
0
,
37
16
0
0
1
0
,
−13
−5
0
0
0
1
forms the basis for the null space of 𝐴.
The 𝑛𝑢𝑙𝑙𝑖𝑡𝑦 𝐴 = 4.

38. Dimension Theorem for Matrices
› If A is a matrix with 𝑛 columns, then
𝑟𝑎𝑛𝑘 𝐴 + 𝑛𝑢𝑙𝑙𝑖𝑡𝑦 𝐴 = 𝑛.
Proof:
If 𝐴 is an 𝑚 𝑥 𝑛 matrix, the nullity of 𝐴 is the dimension of the null
space of 𝐴, that is, the dimension of the solution space of 𝐴𝒙 = 𝟎.
If 𝐴 is transformed to a matrix 𝐵 in reduced row echelon form
having 𝑟 nonzero rows, then we know that the dimension of the
solution space of 𝐴𝒙 = 𝟎 is 𝑛 − 𝑟. Since 𝑟 is also the rank of 𝐴,
then,
𝑛𝑢𝑙𝑙𝑖𝑡𝑦 𝐴 = 𝑛 − 𝑟𝑎𝑛𝑘 𝐴
𝑟𝑎𝑛𝑘 𝐴 + 𝑛𝑢𝑙𝑙𝑖𝑡𝑦 𝐴 = 𝑛.

39. The Sum of Rank and Nullity
Example:
𝐴 =
1 1 1
2 3 4
1
5
Solution:
Clearly, by inspection, the rows of A are linearly
independent. Therefore the rank of A is 2. Since
(rank of A) + (nullity of A) = 4,
it follows that the nullity of A is 2.
Reduced Row Echelon Form:
1 1
2 3
1 1
4 5
0
0
1 1
0 1
1 1
2 3
0
0

40. Fundamental
Matrix Spaces

41. Fundamental Matrix Spaces
(Fundamental Subspaces)
Let 𝐴 be an 𝑚 𝑥 𝑛 matrix.
› Row Space of 𝑨, Row Space of 𝐴𝑇
› Column Space of 𝑨, Column Space of 𝐴𝑇
.
› Null Space of 𝑨, Null Space of 𝑨𝑻
Row Space of 𝐴 = Column Space of 𝐴𝑇
Column Space of 𝐴 = Row Space of 𝐴𝑇

42. Fundamental Matrix Spaces
(Fundamental Subspaces)
Let 𝐴 be an 𝑚 𝑥 𝑛 matrix.
– Row Space of 𝑨
– Column Space of 𝑨
– Null Space of 𝑨
– Null Space of 𝑨𝑻
`Fundamental
Space
Dimension
Row Space of 𝐴 𝑟
Column Space of 𝐴 𝑟
Null Space of 𝐴 𝑛 − 𝑟
Null Space of 𝐴𝑇 𝑚 − 𝑟

43. Thankyou!

44. Exercises
1. Find a basis for the null space of matrix 𝐴.
Then, determine 𝑟𝑎𝑛𝑘 𝐴 and 𝑛𝑢𝑙𝑙𝑖𝑡𝑦 𝐴 .
𝐴 =
1 1 4
0 1 2
0 0 0
1 −1 0
2 1 6
1 2
1 1
1 2
0 2
0 1

45. References
Kolman, B., & Hill, D. R. (2000). Elementary Linear
Algebra. New Jersey: Prentice-Hall, Inc.
Chu, W.-T. (2011, November 14). Lecture 16:4.8
Rank, Nullity, and the Fundamental Matrix
Spaces.
Lecture 18: Rank and Nullity of a Matrix. (n.d.).