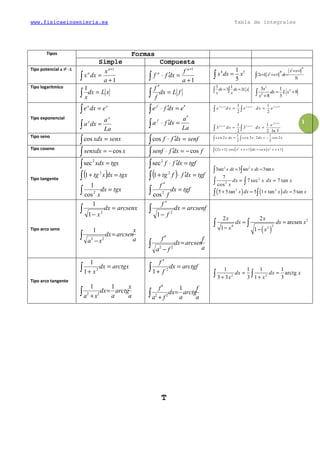
This document provides a methodology for solving definite and indefinite integrals of various types, including simple, logarithmic, exponential, trigonometric, and their inverses. It contains over 40 examples of integrals worked out step-by-step, covering the basic rules for evaluating indefinite integrals of functions like polynomials, trigonometric functions, exponentials, and their inverses.