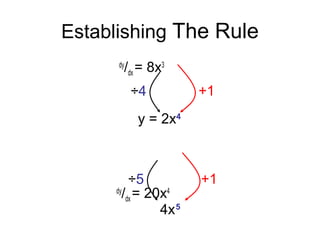
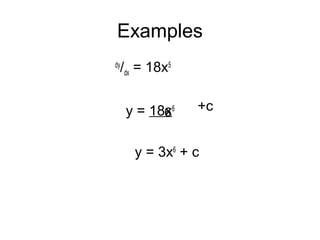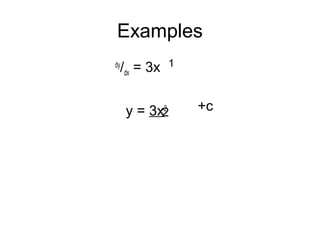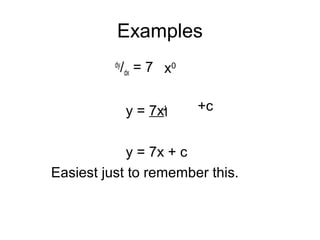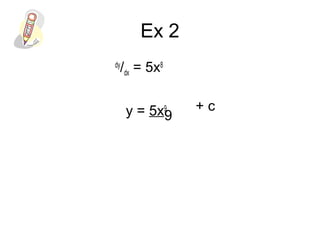This document introduces integration as the reverse process of differentiation. It establishes the rule that if dy/dx = axn, then the integral is y = axn+1/(n+1) + c, where c is the constant of integration. Several examples are worked out applying this rule. The document also introduces notation for integration, including the integral sign ∫ and discusses some cases where the power is not a whole number. It emphasizes that the power in the integral must be positive.

1. Block 2
Integration Introduction

2. What is to be learned?
• Relationship between integration and
differentiation

3. Remember Differentiation
y = 2x3
dy
/dx = 6x2
Integration is Anti Differentiation
dy
/dx = 6x2
y = 2x3

4. Integrating
Find equation for y =
1. dy
/dx = 5x4
2. dy
/dx = 8x3
3. dy
/dx = 6x
4. dy
/dx = 17
y = x5
y = 2x4
y = 3x2
y = 17x
You can always check
by differentiating

5. Another Consideration
y = x2
+ 9
dy
/dx = 2x
y = x2
– 312
dy
/dx = 2x
so integrating dy
/dx = 2x
y = x2 +9– 312+ anything!+ c
where c is a constant
easy to forget!
(General Solution)

6. Finding c
If we are given extra information we can find c.
Ex. dy
/dx = 4x given that y = 20 when x = 3
Find the particular solution.
Integrating y = 2x2
+ c
20 = 2(3)2
+ c
20 = 18 + c
c = 2
Equation is y = 2x2
+ 2
Substituting
(Particular Solution)

7. Finding c
Ex. dy
/dx = 2x + 3 given that y = 16 when x = 4
Find the particular solution.
Integrating y = x2
+ 3x + c
16 = 42
+ 3(4) + c
16 = 28 + c
c = -12
Equation is y = x2
+ 3x – 12
Substituting
(Particular Solution)

8. Integration
Integration is Anti Differentiation
Ex. dy
/dx = 4x
y = 2x2
+ c Easy to forget!

9. Finding c
If we are given extra information we can find c.
Ex. dy
/dx = 2x + 4 is the gradient of the tangent
to a curve which passes through (2 , 10).
Find the equation of the curve
Integrating y = x2
+ 4x + c
10 = (2)2
+ 4(2) + c
10 = 12 + c
c = -2
Equation is y = x2
+ 4x – 2
x y
(General Solution)
Substituting
(Particular Solution)

10. Key Question
Ex. dy
/dx = 4x – 3 given that y = 10 when x = 2
Find the particular solution.
Integrating y = 2x2
– 3x + c
10 = 2(2)2
– 3(2) + c
10 = 2 + c
c = 8
Equation is y = 2x2
– 3x + 8
Substituting
(Particular Solution)

11. What is to be learned?
• Relationship between integration and
differentiation
• The Rule for Integration
• Some terminology and symbol stuff that
we use

12. Establishing The Rule
dy
/dx = 8x3
y = 2x4
+1÷4

13. Establishing The Rule
dy
/dx = 8x3
dy
/dx = 20x4
y = 2x4
+1÷4
5
+1÷5
4x

14. The Rule
dy
/dx = axn
y = axn+1
n+1 +c

15. Examples
dy
/dx = 18x5
y = 18x6
y = 3x6
+ c
6 +c

16. Examples
dy
/dx = 2x3
y = 2x4
y = ½ x4
+ c
or y = x 4
+ c
4 +c
2

17. Examples
dy
/dx = 3x7
y = 3x8
8 +c

18. Examples
dy
/dx = 3x
y = 3x2
2 +c
1

19. Examples
dy
/dx = 7
y = 7x1
y = 7x + c
Easiest just to remember this.
1 +c
x0

20. Introducing The Big S
The integral of 3x2
with respect to x
= x3
+ c
∫ dx

21. Introducing The Big S
4x3
– 4
= x4
– 4x
( )
+ c
∫ dx

22. Integration – The Rule
dy
/dx = axn
y = axn+1
n+1
+c

23. Ex 1
dy
/dx = 24x3
y = 24x4
y = 6x4
+ c
4
+c
Differential
Equation

24. Ex 2
dy
/dx = 5x8
y = 5x9
9
+ c

25. Ex 3
dy
/dx = 9
y = 9x + c
This applies for any number

26. Terminology (The Big S!)
4x + 2
= 2x2
+ 2x
∫ dx( )
+ c
brackets if more
than one thingie

27. Key Question
2x3
– 4x + 7
= ½x4
– 2x2
+ 7x
( )
+ c
∫ dx

28. New Rule – Same Difficulties
∫ √x dx
= ∫ x dx
= x
= 2x
½
3
/2
3
/2
÷ 3
/2  X 2
/3
3
/2
3
+ c
Need a Power!

29. New Rules – Same Difficulties
7 dx
= ∫ 7x-2
dx
= 7x
= -7x
= -7
-1
-1
+ c
x2∫
-1
Power must be on top
Positive Index?
x

30. New Rule – Same Difficulties
∫ 6√x dx
= ∫ 6x dx
= 6x
= (2
/3)6x
= 4x
½
3
/2
3
/2
+ c
Need a Power!
3
/2
3
/2

31. New Rules – Same Difficulties
6 dx
= ∫ 6x-4
dx
= 6x
= -2x
= -2
-3
-3
+ c
x4∫
-3
Power must be on top
Positive Index?
x3

32. New Rule – Same Difficulties
∫ 9√x dx
= ∫ 9x dx
= 9x
= (2
/3)9x
= 6x
½
3
/2
3
/2
÷ 3
/2  X 2
/3
3
/2
+ c
Need a Power!
3
/2

33. New Rules – Same Difficulties
8 dx
= ∫ 8x-3
dx
= 8x
= -4x
= -4
-2
-2
+ c
x3∫
-2
Power must be on top
Positive Index?
x2

34. Key Question
(√x3
– 4 ) dx
= ∫ (x – 4x-7
) dx
= x – 4x-6
= 2
/5x + 2
/3x-6
+ c
= 2
/5x + 2
/3x + c
∫
3
/2
x7
5
/2
5
/2 -6
5
/2
Answer with Positive Indices
6
5
/2