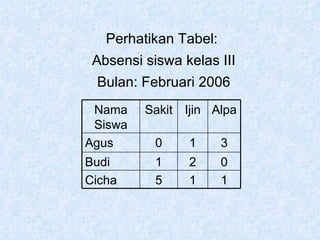
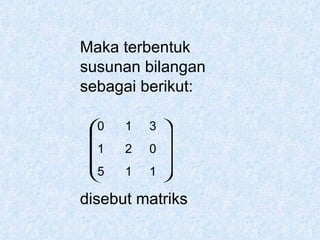
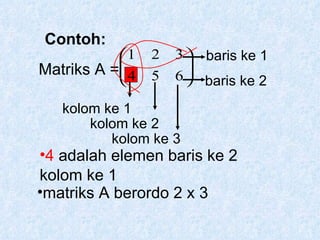
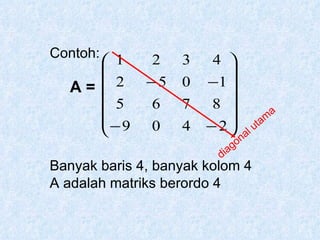
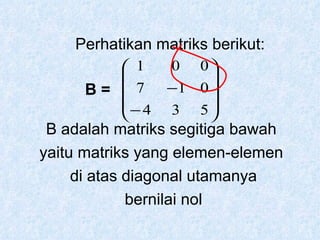
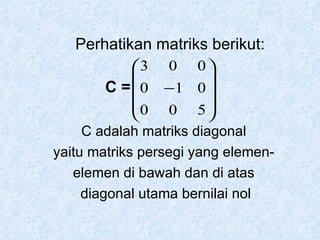
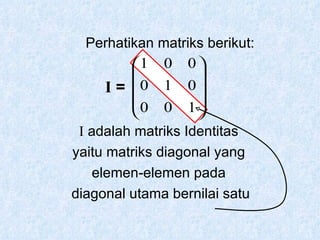
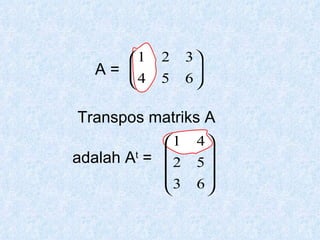
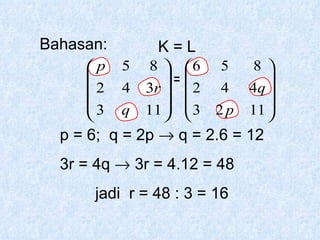
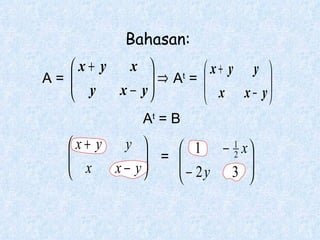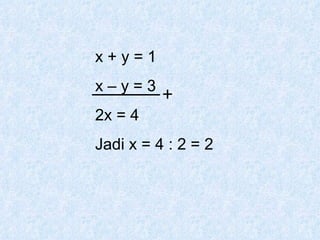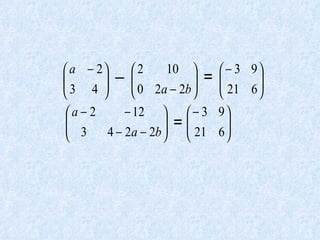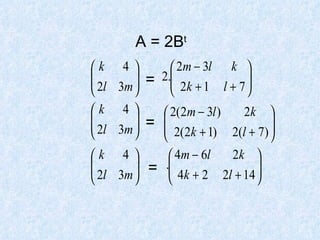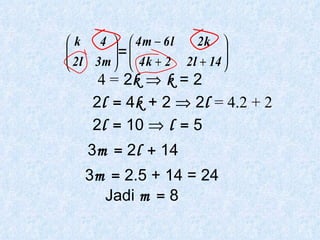Dokumen tersebut membahas tentang pengertian matriks, jenis-jenis matriks seperti matriks persegi, matriks segitiga atas dan bawah, matriks diagonal, matriks identitas, serta operasi-operasi pada matriks seperti penjumlahan, pengurangan, perkalian skalar dan perkalian matriks.

1. MATRIKS

2. Setelah menyaksikan tayangan ini anda dapat menentukan penyelesaian suatu persamaan matrik dengan menggunakan sifat dan operasi matrik

3. Perhatikan Tabel: Absensi siswa kelas III Bulan: Februari 2006 1 1 5 Cicha 0 2 1 Budi 3 1 0 Agus Alpa Ijin Sakit Nama Siswa

4. Jika judul baris dan kolom dihilangkan Judul kolom Judul baris 1 1 5 Cicha 0 2 1 Budi 3 1 0 Agus Alpa Ijin Sakit Nama Siswa

5. Maka terbentuk susunan bilangan sebagai berikut: 0 1 3 1 2 0 5 1 1 disebut matriks

6. Matriks adalah Susunan bilangan berbentuk persegipanjang yang diatur dalam baris dan kolom, ditulis diantara kurung kecil atau siku

7. Bilangan yang disusun disebut elemen. Banyak baris x banyak kolom disebut ordo matriks. Sebuah matriks ditulis dengan huruf besar

8. Contoh: Matriks A = baris ke 1 baris ke 2 kolom ke 1 kolom ke 2 kolom ke 3 matriks A berordo 2 x 3 4 adalah elemen baris ke 2 kolom ke 1

9. Matriks persegi Adalah matriks yang banyak baris dan kolom sama

10. Contoh: Banyak baris 4, banyak kolom 4 A adalah matriks berordo 4 A = diagonal utama

11. A = A adalah matriks segitiga atas yaitu matriks yang elemen-elemen di bawah diagonal utamanya bernilai nol Perhatikan matriks berikut:

12. B = B adalah matriks segitiga bawah yaitu matriks yang elemen-elemen di atas diagonal utamanya bernilai nol Perhatikan matriks berikut:

13. C = C adalah matriks diagonal yaitu matriks persegi yang elemen- elemen di bawah dan di atas diagonal utama bernilai nol Perhatikan matriks berikut:

14. I = I adalah matriks Identitas yaitu matriks diagonal yang elemen-elemen pada diagonal utama bernilai satu Perhatikan matriks berikut:

15. Transpos Matriks Transpos matriks A, ditulis A t adalah matriks baru dimana elemen baris matriks A t merupakan kolom matriks A

16. Transpos matriks A A = adalah A t =

17. Kesamaan Dua Matriks matriks A = matriks B jika ordo matriks A = ordo matriks B elemen yang seletak sama

18. dan B = A = Jika matriks A = matriks B, maka x – 7 = 6  x = 13 2y = -1  y = - ½

19. Contoh 1: Diketahui K = dan L = Jika K = L, maka r adalah….

20. Bahasan: K = L = p = 6; q = 2p  q = 2.6 = 12 3r = 4q  3r = 4.12 = 48 jadi r = 48 : 3 = 16

21. Misalkan A = dan B = Jika A t adalah transpos matriks A maka persamaan A t = B dipenuhi bila x = …. Contoh 2:

22. Bahasan: A = = A t = B A t =

23. x + y = 1 x – y = 3 2x = 4 Jadi x = 4 : 2 = 2 

24. Operasi Pada Matriks Penjumlahan Pengurangan Perkalian:  perkalian skalar dengan matriks  perkalian matriks dengan matriks

25. Penjumlahan/pengurangan  Matriks A dan B dapat dijumlahkan/dikurangkan, jika ordonya sama.  Hasilnya merupakan jumlah/selisih elemen-elemen yang seletak

26. Contoh 1: dan B = A = A + B = + =

27. Jika A = , B = dan C = Maka (A + C) – (A + B) =…. Contoh 2:

28. (A + C) – (A + B) = A + C – A – B = C – B =  = = Bahasan

29. Perkalian skalar dengan matriks  Jika k suatu bilangan (skalar) maka perkalian k dengan matriks A ditulis k. A, adalah matriks yang elemennya diperoleh dari hasil kali k dengan setiap elemen matriks A

30. Matriks A = Tentukan elemen-elemen matriks 5A! Jawab: 5A = Contoh 1:

31. Matriks A = , B = dan C = Jika A – 2B = 3C, maka a + b = …. Contoh 2:

32. = 3 – = A – 2B = 3C – 2 Bahasan

33. – = =

34. = a – 2 = -3  a = -1 4 – 2a – 2b = 6 4 + 2 – 2b = 6 6 – 2b = 6 -2b = 0  b = 0 Jadi a + b = -1 + 0 = -1

35. Matriks A = dan B = Supaya dipenuhi A = 2B t , dengan B t adalah matriks transpos dari B maka nilai m = …. Contoh 3:

36. B = berarti B t = A = 2B t = Bahasan

37. A = 2B t = = =

38. = 4 = 2 k  k = 2 2 l = 4 k + 2  2 l = 4.2 + 2 2 l = 10  l = 5 3 m = 2 l + 14 3 m = 2.5 + 14 = 24 Jadi m = 8