Dokumen tersebut membahas tentang logaritma dan fungsi trigonometri. Secara ringkas, dokumen tersebut memberikan contoh soal logaritma dan pembahasannya, serta menjelaskan hubungan dan rumus dasar dari fungsi trigonometri seperti identitas trigonometri, rumus jumlah dan selisih sudut, serta rumus perkalian.

1. LOGARITMA
Soal No. 1
Ubah bentukpangkatpada soal-soal berikutmenjadi bentuklogaritma:
a) 23
= 8
b) 54
= 625
c) 72
= 49
Pembahasan
Transformasi bentukpangkatke bentuklogaritma:
Jika ba
= c, maka b
logc = a
a) 23
= 8 → 2
log8 = 3
b) 54
= 625 → 5
log625 = 4
c) 72
= 49 → 7
log49 = 2
Soal No. 2
Tentukannilai dari:
a) 2
log8 + 3
log9 + 5
log125
b) 2
log 1/8 + 3
log1/9 + 5
log1/125
Pembahasan
a) 2
log8 + 3
log9 + 5
log125
= 2
log23
+ 3
log32
+ 5
log53
= 3 2
log2 + 2 3
log3 + 3 5
log5
= 3 + 2 + 3 = 8
b) 2
log 1
/8 + 3
log1
/9 + 5
log1
/125
= 2
log2−3
+ 3
log 3−2
+ 5
log5−3
= − 3 − 2 − 3 = − 8
Soal No. 3
Tentukannilai dari
a) 4
log8 + 27
log9
b) 8
log 4 + 27
log1/9
Pembahasan
a) 4
log8 + 27
log9
= 22
log23
+ 33
log32
= 3/2 2
log 2 + 2/3 3
log3
= 3/2 + 2/3 = 9/6 + 4/6 = 13/6
b) 8
log 4 + 27
log1/9
23
log22
+ 33
log3−2
= 2/3 2
log 2 + (−2/3) 3
log3
= 2/3 − 2/3 = 0
Soal No. 4
Tentukannilai dari:

2. a) √2
log 8
b) √3
log 27
Pembahasan
a) √2
log 8
= 21/2
log23
= 3/0,5 2
log2 = 3/0,5 = 6
b) √3
log 9
= 31/2
log32
= 2/0,5 3
log3 = 2/0,5 = 4
Soal No. 5
Diketahui:
logp = A
logq = B
Tentukannilai dari logp3
q2
Pembahasan
logp3
q2
= log p3
+ log q2
= 3 logp + 2 log q = 3A + 2B
Soal No. 6
Diketahui
log40 = A dan log2 = B, tentukannilai dari log20
Pembahasan
log20 = log40/2 = log 40 − log2 = A − B
Soal No. 7
Diketahui 2
log7= a dan 2
log3 = b. Tentukannilai dari 6
log14
Pembahasan
2
log7 = a
log 7
/log 2 = a
log7 = a log2
2
log3 = b
log 3
/log 2 = b
log3 = b log2
6
log14 = log 14
/log6
log2.7 log 2 + log 7 log 2 + a log 2 log 2 (1 + a) (1 + a)
=_________ = ________________
=__________________
=________________
=_________
log2. 3 log 2 + log3 log 2 + b log 2 log 2 (1 + b) (1 + b)
Soal No. 8
Diketahui 2
log√(12 x + 4) = 3. Tentukannilai x

3. Pembahasan
2
log√ (12 x + 4) = 3
Ruas kiri bentuknyalog,ruaskananbelumbentuklog,ubahduluruaskananagar jadi bentuklog. Ingat
3 itusama jugadengan2
log23
. Ingat rumus a
log ab
= b jadi
2
log√( 12 x + 4) = 2
log23
Kiri kanansudahbentuklogdenganbasisyangsama-samadua, hinggatinggal menyamakanyangdi
dalamlog kiri-kananataucoretajalognya:
2
log√( 12 x + 4) = 2
log23
√( 12 x + 4) = 23
√( 12 x + 4) = 8
Agar hilangakarnya,kuadratkankiri,kuadratkankanan.Yangkiri jadi hilangakarnya:
12 x + 4 = 82
12x + 4 = 64
12 x = 60
x = 60
/12 = 5
Soal No. 9
Tentukannilai dari 3
log5
log125
Pembahasan
3
log5
log125 = 3
log5
log 53
= 3
log3 = 1
Soal No. 10
Diketahui 2
log3 = m dan 2
log5 = n . Tentukannilai dari 2
log90
Pembahasan
log 3
2
log3 = _______ = m Sehingga log 3 = m log 2
log 2
log 5
2
log5 = _______ = n Sehingga log 5 = n log 2
log 2
log32
. 5 . 2 2 log 3 + log 5 + log 2
2
log90 =___________________ = ______________________________
log 2 log 2
2 m log 2 + n log 2 + log 2
2
log90 =_________________________________________ = 2 m + n + 1
log 2
Soal No. 11
Nilai dari
A. 1
B. 2
C. 3
D. 5
E. 6
Pembahasan

4. Dari sifatlogaritmaberikut:
Soal disederhanakanmenjadi
Soal No. 12
Nilai dari
A. 1
B. 2
C. 3
D. 5
E. 6
Pembahasan
Dari sifatyangsama:
Diperolehhasil
1) Jika log 2 = a
maka log 5 adalah …
jawab :
log 5 = log (10/2) = log 10 – log 2 = 1 – a (karena log 2 = a)

5. 2) √15 + √60 - √27 = ...
Jawab :
√15 + √60 - √27
= √15 + √(4x15) - √(9x3)
= √15 + 2√15 - 3√3
= 3√15 - 3√3
= 3(√15 - √3)
3) log 9 per log 27 =...
Jawab :
log 9 / log 27
= log 3² / log 3³
= (2. log 3) / (3 . log 3) <-- ingat sifat log a^n = n. log a
= 2/3
4) √5 -3 per √5 +3 = ...
Jawab :
(√5 - 3)/(√5 + 3)
= (√5 - 3)/(√5 + 3) x (√5 - 3)/(√5 - 3) <-- kali akar sekawan
= (√5 - 3)²/(5 - 9)
= -1/4 (5 - 6√5 + 9)
= -1/4 (14 - 6√5)
= -7/2 + 3/2√5
= (3√5 - 7)/2
5) Jika a log 3 = -0,3 tunjukkan bahwa a = 1/81 3√9
Jawab :
ª log 3 = -0,3
log 3/log a = -0.3
log a = -(10/3)log 3
log a = log [3^(-10/3)]
a = 3^(-10/3) = 3^(-4) (3²)^(⅓ )
a= 1/81 3√9
TERBUKTI ^_^
6) log (3a - √2) dengan basis 1/2. Tentukan nilai a!
Jawab :
[log (3a - √2)]/log(0.5) = -0.5

6. log (3a - √2) = -0.5 log 0.5 = log (1/√½)
3a - √2 = 1/√½
a = (2/3) √2
7) Jika , maka .
Penyelesaian :
Langkah pertama :
Langkah kedua :
selesai
8) Diketahui dan , maka .
Penyelesaian :
Kemudian :
selesai
9)Supaya terdefinisi maka haruslah ….
A. x < 2 atau x > 3
B. 0 < x < 2 atau x > 3
C. 0 < x < 1 atau x > 3
D. 0 < x < 1 atau 1 < x < 2
E. 0 < x < 1 atau 1 < x < 2 atau x > 3
Penyelesaian :
Ingat bahwa terdefinisi jika p, q > 0. Sehingga
Jawab (C)
Dengan merasionalkan penyebut, bentuk sederhana dari adalah …
A. 2 – 3
B. 3 – 3
C. 3 – 2

7. D. 4 – 2
E. 4 + 2
PEMBAHASAN :
= x
=
= 2 – 3
JAWABAN : A
= …
A. 24 32
B. 27 32
C. 26 35
D. 28 32
E. 28 35
PEMBAHASAN :
= 23 3-2 2 34
= 23+1 3-2+4
= 24 32
JAWABAN : A
Bentuk pangkat bulat positif dari adalah …

8. A.
B.
C.
D.
E.
PEMBAHASAN :
=
JAWABAN : B
Dengan merasionalkan penyebut, bentuk sederhana dari adalah …
A. –7 – 4
B. –7 –
C. 7 – 4
D. 7 + 4
E. 7 –
PEMBAHASAN :
=
=

9. = 7 – 4
JAWABAN : C
Nilai x yang memenuhi persamaan 4x+1 = 8x-1 adalah …
A. 3
B. 4
C. 5
D. 6
E. 7
PEMBAHASAN :
4x+1 = 8x-1
22(x+1) = 23(x-1)
22x+2 = 23x-3
2x + 2 = 3x – 3
5 = x
JAWABAN : C
Nilai dari 2log 3 – 2log 6 + 2log 8 = …
A. 1
B. 2
C. 3
D. 4
E. 5
PEMBAHASAN :

10. 2log 3 – 2log 6 + 2log 8 = 2log [(3 : 6) x 8]
= 2log 4
= 2log 22
= 2 2log 2
= 2
JAWABAN : B
Jika 2log 3 = x dan 3log 5 = y , maka 4log 15 = …
A. xy + 1
B.
C.
D.
E.
PEMBAHASAN :
4log 15 =
=
=
=

11. =
=
=
JAWABAN : C
Jika = a + b dengan a dan b bilangan bulat, maka a + b = …
A. -5
B. -3
C. -2
D. 2
E. 3
PEMBAHASAN :
=
=
=
= -5 + 2
jadi a = -5 dan b = 2, sehingga
a + b = -5 + 2 = -3
JAWABAN : B

12. Jika 2log a + 2log b = 12 dan 3.2log a – 2log b = 4, maka a + b = …
A. 144
B. 272
C. 528
D. 1.024
E. 1.040
PEMBAHASAN :
2log a + 2log b = 12
2log [a.b] = 12
a.b = 212 … (i)
3.2log a – 2log b = 4
2log a3 – 2log b = 4
2log [a3 : b] = 4
a3 : b = 24
a3 : 24 = b … (ii)
substitusi (ii) ke (i), diperoleh
a.[ a3 : 24] = 212
a4 = 212.24
a4 = 216
a = 24 … (iii)
substitusi (iii) ke (ii), sehingga diperoleh
(24)3 : 24 = b

13. 28 = b
a + b = 24 + 28
= 16 + 256
= 272
JAWABAN : B
Jika a = 8 dan b = 9, maka a-1/3.b1/2 = …
A. 4/3
B. 4/3
C. 2/3
D. 3/4
E. 3/2
PEMBAHASAN :
a-1/3.b1/2 = 8-1/3.91/2
= (23)-1/3.(32)1/2
= 2-1.3
= 3/2
JAWABAN : E
Jika 3log a + 3log b = 8 dan 3.3log a – 3log b = 4, maka a + b = ….
A. 9
B. 27
C. 81
D. 243

14. E. 729
PEMBAHASAN :
3log a + 3log b = 8
3log [a.b] = 8
a.b = 38 … (i)
3.3log a – 3log b = 4
3log a3 – 3log b = 4
3log [a3 : b] = 4
a3 : b = 34
a3 : 34 = b … (ii)
substitusi (ii) ke (i), diperoleh
a.[ a3 : 34] = 38
a4 = 38.34
a4 = 212
a = 33 … (iii)
substitusi (iii) ke (ii), sehingga diperoleh
(33)3 : 34 = b
35 = b
a + b = 33 + 35
= 27 + 243
= 270
JAWABAN :

15. Hubungan fungsi trigonometri[sunting | sunting sumber]
Fungsi dasar:
Identitas trigonometri[sunting | sunting sumber]
Rumus jumlah dan selisih sudut[sunting | sunting sumber]
Rumus perkalian trigonometri[sunting | sunting sumber]

16. Rumus jumlah dan selisih trigonometri[sunting | sunting sumber]
Rumus sudut rangkap dua[sunting | sunting sumber]
Rumus sudut rangkap tiga[sunting | sunting sumber]
Rumus setengah sudut[sunting | sunting sumber]
Nyatakan perbandingan trigonometri berikut ini dalam perbandingan
trigonometri sudutlancip!
a. sin 134o
b. cos 151o
c. tan 99o
d. cot 161o
e. sec 132o
f. cosec 147o
Pembahasan

17. Sudutlancip merupakan sudutyang berada pada kuadran I sehingga sudutpada
soal harus kita ubah menjadi sudutkuadran I dengan mengunakan rumus untuk
sudut(90o
+ αo
). Ingatbahwa untuk sudutkuadran II hanya sinus dan cosecan
yang bernilai positif.
sin 134o
=sin (90o
+44o
)
⇒ sin 134o
=cos 44o
Jadi, sin 134o
=cos 44o
.
cos 151o
= cos (90o
+ 61o
)
⇒ cos 151o
=-sin 61o
Jadi, cos 151o
= -sin 61o
tan 99o
= tan (90o
+ 9o
)
⇒ tan 99o
= -cot 9o
Jadi, tan 99o
= -cot 9o
cot 161o
= cot (90o
- 71o
)
⇒ cot 161o
=-tan 71o
Jadi, cot 161o
= -tan 71o
sec 132o
=sec (90o
- 42o
)
⇒ sec 132o
= -cosec 42o
Jadi, sec 132o
=-cosec 42o
cosec 147o
= cosec (90o
- 57o
)
⇒ cosec 147o
=sec 57o
Jadi, cosec 147o
= sec 57o
Dengan menggunakan rumus perbandingan triogonometriuntuk sudut(90o
+αo
),
hitunglah nilai dari setiap perbandingan trigonometriberikut ini!
a. sin 135o
b. cos 150o
c. tan 120o
Pembahasan
sin 134o
=sin (90o
+45o
)

18. ⇒ sin 134o
=cos 45o
Jadi, sin 134o
=½√2.
cos 150o
= cos (90o
+ 60o
)
⇒ cos 150o
=-sin 60o
Jadi, cos 150o
= -½√3.
tan 120o
= tan (90o
+ 30o
)
⇒ tan 120o
=-cot 30o
Jadi, tan 120o
= -√3.
Sederhanakanlah setiap bentuk berikut ini :
a. cos (90o
- αo
) / sin (90o
- αo
)
b. sec (90o
- αo
) / cosec (180o
+αo
)
c. sin (90o
- αo
) / sin (90o
+ αo
)
d. sin (180o
- αo
) / sin (90o
- αo
)
e. cos (90o
+αo
) / cosec (180o
- αo
)
Pembahasan
cos (90o
- αo
) / sin (90o
- αo
) = sin αo
/ cos αo
⇒ cos (90o
- αo
) / sin (90o
- αo
) = tan αo
Jadi, cos (90o
- αo
) / sin (90o
- αo
) = tan αo
.
sec (90o
- αo
) / cosec (180o
+αo
) = cosec αo
/ -cosec αo
⇒ sec (90o
- αo
) / cosec (180o
+αo
) = -1
Jadi, sec (90o
- αo
) / cosec (180o
+ αo
) = -1
sin (90o
- αo
) / sin (90o
+αo
) = cos αo
/ cos αo
⇒ sin (90o
- αo
) / sin (90o
+ αo
) = 1
Jadi, sin (90o
- αo
) / sin (90o
+ αo
) = 1
sin (180o
- αo
) /sin (90o
- αo
) = sin αo
/ cos αo
⇒ sin (180o
- αo
) / sin (90o
- αo
) = tan αo
Jadi, sin (180o
- αo
) /sin (90o
- αo
) = tan αo
cos (90o
+ αo
) / cosec (180o
- αo
) = -sin αo
/ cosec αo

19. ⇒ cos (90o
+αo
) / cosec (180o
- αo
) = -sin αo
/ (1/sin αo
)
Jadi, cos (90o
+ αo
) / cosec (180o
- αo
) =- sin2
αo
Jika α, β, dan γ adalah sudut-sudutdalam segitiga ABC, tunjukkanlah bahwa :
a. sin (β + γ) = sin α
b. cos (β + γ) = -cos α
c. tan (β + γ) = -tan α
Pembahasan
Ingatbahwa dalam segitiga jumlah sudutnya samdengan 180o
, sehingga berlaku :
α + β + γ = 180o
, → β + γ = 180o
- α.
sin (β + γ) = sin α
⇒ sin (180o
- α) = sin α
⇒ sin α = sin α
Terbukti.
cos (β + γ) = -cos α
⇒ cos (180o
- α) = -cos α
⇒ -cos α = -cos α
Terbukti.
tan (β + γ) = -tan α
⇒ tan (180o
- α) = -tan α
⇒ -tan α = -tan α
Soal dan Pembahasan TrigonometriSudut berelasi
Nyatakanlah perbandingan trigonometri berikut ini ke dalam perbandingan
trigonometri sudutkomplemennya!
a. sin 52o
b. cos 16o
c. tan 57o
d. cot 28o
e. sec 56o
f. cosec 49o
Pembahasan

20. Perhatikan bahwa semua sudutyang ditanya berada pada kuadran I sehingga
semua nilai perbandingan trigonometrinya positif.
sin 52o
= sin (90o
- 38o
)
⇒ sin 52o
= cos 38o
Jadi, sin 52o
= cos 38o
.
cos 16o
= cos (90o
- 74o
)
⇒ cos 16o
= sin 74o
Jadi, cos 16o
= sin 74o
tan 57o
= tan (90o
- 33o
)
⇒ tan 57o
= cot 33o
Jadi, tan 57o
= cot 33o
cot 28o
= cot (90o
- 62o
)
⇒ cot 28o
= tan 62o
Jadi, cot 28o
= tan 62o
sec 56o
= sec (90o
- 34o
)
⇒ sec 56o
= cosec 34o
Jadi, sec 56o
= cosec 34o
cosec 49o
= cosec (90o
- 41o
)
⇒ cosec 49o
= sec 41o
Jadi, cosec 49o
= sec 41o
RumusPenyelesaianPersamaan
Trigonometri
Untuk sinus
Untuk kosinus

21. Untuk tangen
k diisi nilai 0,1, 2, 3 dan seterusnya.
Contoh:
Soal No.1
Untuk 0° ≤ x ≤ 360° tentukanhimpunanpenyelesaiandari sinx = 1
/2
Pembahasan
Dari:
sinx = 1
/2
Untuk harga awal,sudutyangnilai sinnya1
/2 adalah30°.
Sehingga
sinx = 1
/2
sinx = sin 30°
Denganpolarumusyang pertamadi atas:
(i) x = 30 + k ⋅ 360
k = 0 → x = 30 + 0 = 30 °
k = 1 → x = 30 + 360 = 390 °

22. (ii) x = (180 − 30) + k⋅360
x = 120 + k⋅360
x = 150 + k⋅360
k = 0 → x = 150 + 0 = 150 °
k = 1 → x = 150 + 360 = 510 °
Dari penggabunganhasil (i) danhasil (ii),denganbataspermintaan0°≤ x ≤ 360°, yangdiambil sebagai
himpunanpenyelesaiannyaadalah:
HP = {30°, 150°}
Soal No.2
Untuk 0° ≤ x ≤ 360° tentukanhimpunanpenyelesaiandari cosx = 1
/2
Pembahasan
1
/2 adalah nilai cosinusdari 60°.
Sehingga
cos x = cos 60°
(i) x = 60° + k ⋅ 360°
k = 0 → x = 60 + 0 = 60 °
k = 1 → x = 60 + 360 = 420°
(ii) x = −60° + k⋅360
x = −60 + k⋅360
k = 0 → x = −60 + 0 = −60°
k = 1 → x = −60 + 360° = 300°
Himpunanpenyelesaianyangdiambil adalah:
HP = {60°, 300°}
Soal No.3
Untuk 0° ≤ x ≤ 720° tentukanhimpunanpenyelesaiandari sin(x −30) = 1
/2 √3
Pembahasan
1
/2 √3 miliknyasin60°

23. Sehingga
sin(x − 30) = sin60°
dan
Untuk 0° ≤ x ≤ 720°, HP = {90°, 150°, 450°, 510°}
Soal No.4
Untuk 0° ≤ x ≤ 360° tentukanhimpunanpenyelesaiandari
cos (x − 30°) = 1
/2 √2
Pembahasan
Harga awal untuk 1
/2 √2 adalah 45°
HP = {75°, 345°}
Soal No.5

24. Himpunanpenyelesaianpersamaan:
cos 2x + sinx = 0
untuk0 < x ≤ 2π adalah.....
A. {π/2,4π/3, 5π/3}
B. {π/2, 7π/6, 4π/3}
C. {π/2, 7π/6, 5π/3}
D. {π/2, 7π/6, 11π/6}
E. {π/2, 5π/3, 11π/6}
Pembahasan
Dari rumussudutrangkap dari pelajaransebelumnya:
cos 2x = cos2
x − sin2
x
cos 2x = 2 cos2
x − 1
cos 2x = 1 − 2 sin2
x
cos 2x + sinx = 0
1 − 2 sin2
x + sinx = 0
− 2 sin2
x + sinx + 1 = 0
2 sin2
x − sinx − 1 = 0
Faktorkan:
(2sinx + 1)(sinx − 1) = 0
2sin x + 1 = 0
2sin x = −1
sinx = −1
/2
x = 210° dan x = 330°
atau
sinx − 1 = 0
sinx = 1
x = 90°
Sehingga:
HP = {90°, 210°, 330°} dalamsatuanderajat.
HP = {π/2,7π/6, 11π/6} dalamsatuan radian.
Jawaban :D.
Soal No.6
Himpunanpenyelesaianpersamaan cos2x + 5 sinx + 2 = 0 untuk0 ≤ x ≤ 2π adalah…
A. {2π/3,4π/3}
B. {4π/3, 5π/3}
C. {5π/6, 7π/6}
D. {5π/6, 11π/6}
E. {7π/6, 11π/6}

25. Pembahasan
Persamaantrigonometri:
Misalkansinx sebagai Pdan jugacos 2x = 1 − 2sin2
x
Soal No.7
Himpunanpenyelesaianpersamaan 2cos2
x − 3 cos x + 1 = 0 untuk0 < x < 2π adalah…
A. {π/6,5π/6}
B. {π/6, 11π/6}
C. {π/3, 2π/3}
D. {π/3, 5π/3}
E. {2π/3, 4π/3}
Pembahasan
2cos 2
x − 3 cos x + 1 = 0
Faktorkan:
(2cos x − 1)(cos x − 1) = 0
(2cos x − 1) = 0
2cos x = 1
cos x = 1/2
x = 60° = π/3 danx = 300° = 5π/3
atau
(cosx − 1) = 0 cos x = 1
x = 0° dan x = 360° = 2π (Tidakdiambil,karenadiminta0< x < 2π)
Jadi HP = {π/3, 5π/3}
Jawaban:D
Soal No.8
Himpunanpenyelesaiandari persamaancos4x + 3 sin2x = −1 untuk0° ≤ x ≤ 180° adalah…
A. {150°,165°}
B. {120°,150°}
C. {105°,165°}

26. D. {30°,165°}
E. (15°,105°)
Pembahasan
Ubah ke bentuksinsemua,denganrumussudutrangkap,kemudianfaktorkan:
cos 4x + 3 sin 2x = −1
Untuk faktor
TidakMemenuhi,lanjutke faktor
Diperoleh
Jadi HP = {105°,165°}
Soal No.9
Himpunanpenyelesaiandari 2sin2
x − 3 sinx + 1 = 0 dengan0° ≤ x ≤ 360° adalah....
A. {30°, 90°, 150°}
B. {30°, 120°, 240°}
C. {30°, 120°, 300°}
D. {30°, 150°, 270°}
E. {60°, 120°, 270°}
(UN Matematika SMA IPA 2014)
Pembahasan
Soal ini akan coba diselesaikandengancaracoba-coba.Ambil salahsatusudutdari pilihanjawabanyang
ada, untukmengeliminirpilihanlainnya.Dari yangmudahyaitu30° atau 90°. Nilai sin30° adalah1/2,
jikasudutini termasukjawabanmakaakan samadengannol seperti permintaansoal.
Persamaandi soal:
2 sin2
x − 3 sinx + 1 = ?

27. 30° → 2 sin2
(30°) − 3 sin(30°) + 1 = ?
= 2 (1/2)2
− 3 (1/2) + 1
= 0 (Benar,jadi jawabanharusmemuatangka 30°, pilihanEsalahkarenatidakmemuat30 derajad.)
Berikutnyacoba90°, tentunyasudahtahusin90° = 1
2 sin2
x − 3 sinx + 1 = ?
90° → 2 sin2
90° − 3 sin90° + 1 = ?
= 2 (1)2
− 3 (1) + 1
= 2 − 3 + 1
= 0 (Benar,Jawabanharus memuat90° jadi B, C, D, dan E salah,A dipastikanbenartanpadilakukan
pengecekanpada150°, tentunyakalausoalnyandak error)
Soal No.10
Himpunanpenyelesaianpersamaancos2x − 2 sinx = 1; 0 ≤ x < 2π adalah....
A. {0, π, 3π/2, 2π}
B. {0, π, 4π/3, 2π}
C. {0, 2π/3; π, 2π}
D. {0, π, 2π}
E. {0, π, 3π/2}
Pembahasan
Soal ini lebihmudahlagi,syaratnyaadalah0 ≤ x < 2π , maka x tidakbolehmemuat2π,karenatandanya
adalahlebihkecil dari 2π bukanlebihkecil atausamadengan.Jadi pilihanyangada2π nya salah,hanya
E yang tidakmemuat2π. Jadi jawabnyayang E, soal di atas dari soal UN, namunsoal seperti ini jarang-
jarang ada
Rumus Statistika Matematika
1. Rumus Rataan Hitung (Mean)
Rata-rata hitung dihitung dengan cara membagi jumlah nilai data dengan banyaknya data. Rata-rata
hitung bisa juga disebut mean.
a) Rumus Rataan Hitung dari Data Tunggal
b) Rumus Rataan Hitung Untuk Data yang Disajikan Dalam Distribusi Frekuensi

28. Dengan : fixi = frekuensi untuk nilai xi yang bersesuaian
xi = data ke-i
c) Rumus Rataan Hitung Gabungan
2. Rumus Modus
a. Data yang belum dikelompokkan
Modus dari data yang belum dikelompokkan adalah ukuran yang memiliki frekuensi tertinggi. Modus
dilambangkan mo.
b. Data yang telah dikelompokkan
Rumus Modus dari data yang telah dikelompokkan dihitung dengan rumus:
Dengan : Mo = Modus
L = Tepi bawah kelas yang memiliki frekuensitertinggi (kelas modus) i = Interval kelas
b1 = Frekuensi kelas modus dikurangi frekuensi kelas interval terdekat sebelumnya
b2 = frekuensi kelas modus dikurangi frekuensikelas interval terdekat sesudahnya
3. Rumus Median (Nilai Tengah)
a) Data yang belum dikelompokkan
Untuk mencari median, data harus dikelompokan terlebih dahulu dari yang terkecil sampai yang
terbesar.

29. b) Data yang Dikelompokkan
Dengan : Qj = Kuartil ke-j
j = 1, 2, 3
i = Interval kelas
Lj = Tepi bawah kelas Qj
fk = Frekuensi kumulatif sebelum kelas Qj
f = Frekuensi kelas Qj
n = Banyak data
4. Rumus Jangkauan ( J )
Selisih antara nilai data terbesar dengan nilai data terkecil.
5. Rumus Simpangan Quartil (Qd)
6. Rumus Simpangan baku ( S )
7. Rumus Simpangan rata – rata (SR)
8. Rumus Ragam (R)

30. Contoh soal statistika
Tabel 1.1 dibawah ini:
Jawab :

31. Soal No. 1
Diberikan data sebagai berikut:
6, 6, 7, 8, 9, 10
Tentukan nilai rerata data di atas!
Pembahasan
Mencari rerata untuk data tunggal, jumlahkan datanya kemudian dibagi dengan
banyaknya data.
Sehingga
Soal No. 2
Perhatikan tabel distribusi frekuensi data tunggal berikut ini

32. Nilai frekuensi (f)
5
6
7
8
9
2
5
11
8
4
Tentukan rata-rata!
Pembahasan
Mencari rata-rata untuk data tunggal dengan diketahui frekuensi,
Sehingga
Soal No. 3
Perhatikan tabel berikut!
Berat (kg) Frekuensi
31 - 35
36 - 40
41 - 45
46 - 50
51 - 55
56 - 60
61 - 65
4
6
9
14
10
5
2
Tentukan rata-ratanya!
Pembahasan
Ambil titik tengah untuk setiap interval kelas terlebih dahulu:
Berat (kg)
Titik Tengah
(x)
Frekuensi
(f)

33. 33
38
43
48
53
58
63
4
6
9
14
10
5
2
Setelah titik tengah ditentukan, dengan rumus yang sama soal nomor 2:
Diperoleh nilai rerata:
Soal No. 4
Perhatikan tabel distribusi frekuensi data berkelompok berikut!
Berat (kg) Frekuensi
31 - 35
36 - 40
41 - 45
46 - 50
51 - 55
56 - 60
61 - 65
4
6
9
14
10
5
2
Dengan cara atau metode rataan sementara, tentukan nilai rata-rata data di atas!
Pembahasan
Soal ini sama persis soal nomor 3, tapi disuruh menggunakan rataan sementara.
Tentukan titik tengah tiap kelas dulu seperti soal sebelumnya,..
Berat (kg)
Titik Tengah
(x)
Frekuensi
(f)
33
38
4
6

34. 43
48
53
58
63
9
14
10
5
2
Setelah itu, tentukan rataan sementara yang hendak dipakai, misalkan disini diambil 48
sebagai rataan sementara,
x̅s = 48
Buat kolom baru lagi, isinya titik tengah setiap kelas dikurangi rataan sementara (x − x̅s),
di kolom namakan sebagai d saja:
Berat (kg)
Titik Tengah
(x)
Frekuensi
(f)
d
33
38
43
48
53
58
63
4
6
9
14
10
5
2
− 15
− 10
− 5
0
5
10
15
Langkah berikutnya, tambah kolom baru di kanan, isinya perkalian tiap-tiap frekuensi
dengan d tadi kemudian jumlahkan.
Berat (kg)
Titik Tengah
(x)
Frekuensi
(f)
d f ⋅ d
33
38
43
48
53
58
63
4
6
9
14
10
5
2
− 15
− 10
− 5
0
5
10
15
− 60
− 60
− 45
0
50
50
30
Jumlahnya:
Σ fi = 4 + 6 + 9 + 14 + 10 + 5 + 2 = 50
Σ fi ⋅ di = − 60 − 60 − 45 + 0 + 50 + 50 + 30 = − 35
Terakhir rata-ratanya adalah:

35. Sehingga diperoleh
Soal No. 1
Diberikan data sebagai berikut:
6, 7, 8, 8, 10, 9
Tentukan:
a) Ragam (variansi)
b) Simpangan baku
Pembahasan
Pertama kali cari rata-ratanya dulu:
Sehingga
a) Ragam (variansi)
Untuk menentukan ragam atau variansi (S2
) ,
Sehingga

36. b) Simpangan baku Simpangan baku (S) adalah akar dari ragam
Sehingga diperoleh nilai simpangan baku data di atas
Soal No. 2
Perhatikan tabel distribusi frekuensi data tunggal berikut ini
Nilai frekuensi (f)
5
6
7
8
9
2
5
12
7
4
Tentukan:
a) Ragam (variansi)
b) Simpangan baku
Pembahasan
Pertama kali cari rata-ratanya dulu:
Sehingga
a) Ragam (variansi)
Untuk menentukan ragam atau variansi (S2
) ,

37. Sehingga
b) Simpangan baku Simpangan baku (S) adalah akar dari ragam
Sehingga diperoleh nilai simpangan baku data di atas
Soal No. 3
Perhatikan tabel berikut!
Berat (kg) Frekuensi
31 - 35
36 - 40
41 - 45
46 - 50
4
7
9
10
Tentukan:
a) Ragam (variansi)
b) Simpangan baku
Pembahasan
Ambil titik tengah untuk setiap interval kelas terlebih dahulu:
Berat (kg)
Titik Tengah
(x)
Frekuensi
(f)
33
38
43
4
7
9

38. 48 10
Setelah titik tengah ditentukan, cari rata-rata dulu:
Diperoleh nilai rerata:
a) Ragam (variansi)
Untuk menentukan ragam atau variansi (S2
) ,
Sehingga
b) Simpangan baku Simpangan baku (S) adalah akar dari ragam
Sehingga diperoleh nilai simpangan baku data di atas

39. Konsep Perkalian Matriks
Bila,matriks A dan B seperti diberikan di bawah ini,maka A.B adalah sebagai
berikut :

40. Dari contoh di atas dapat dilihat bahwa ordo hasil kali dua buah matriks
bergantung pada banyak baris matriks pertama dan banyak kolom matriks
kedua.
Amxn . Bnxk = Cmxk
Misal :
A2x3 dikali dengan B3x3 akan menghasilkan matriks C2X3
A3X4 dikali dengan B4x2 akan menghasilkan matriks C3X2
A3X1 dikali dengan B1x3 akan menghasilkan matriks C3X3
A1X3 dikali dengan B3X1 akan menghasilkan matriks C1X1
Kumpulan Soal :
1. Matriks A dan B masing-masing seperti di bawah ini. Tentukan A.B dan B.A
Pembahasan :
A2X2 dikali dengan B2X2 akan menghasilkan matriks 2x2.

41. B2X2 dikali dengan A2X2 akan menghasilkan matriks 2x2.
Dari hasil yang diperoleh dapat kita lihat bahwa AB ≠ BA
2. Matriks P dan Q adalah sebagai berikut :
Pembahasan :
P2X3 dikali dengan Q3X3 akan menghasilkan matriks 2x3.

42. 3. Tentukan hasil kali K.M jika K dan M seperti di bawah ini.
Pembahasan :
K3X1 dikalikan dengan M1X3 akan menghasilkan matriiks 3x3

43. 4. Matriks A dan B masing-masing seperti di bawah ini. Tentukan A.B
Pembahasan :
A1X3 dikali dengan B3X1 akan menghasilkan matriks 1x1
5. Tentukan hasil dari A.B :
Pembahasan :
A4X3 dikali dengan B3X2 akan menghasilkan matriks ordo 4x2

44. 6. Bila matriks A merupakan matriks 2x2 seperti di bawah ini, maka tentukanlah
A2
Pembahasan :

45. 7. Buktikan bahwa A.I = I.A. Dengan matriks A seperti pada soal no 6 dan I matriks
identitas 2x2.
Pembahasan :
8. Tentukan A.B jika A dan B seperti di bawah ini.
Pembahasan :
Karena A2X2 dan B2X1 maka hasilnya adalah matriks ordo 2x1 seperti ini.
9. Berikan dua matriks A dan B yang memenuhi persamaan (A+B)2
= A2
+ B2

46. Pembahasan :
(A+B)2
= A2
+ B2
A2
+ AB + BA + B2
= A2
+ B2
---> ingat bahwa pada matriks belum tentu AB = BA
A2
+ B2
- A2
- B2
+ AB + BA = 0
AB + BA = 0
Untuktujuan praktis,anggaplah AB = 0 dan BA = 0 dengan begitu AB + BA = 0.
Beberapa syarat agar AB = BA = 0 antara lain :
o Kedua matriks merupakan matriks persegi yang memiliki ordo sama karena jika
ordo berbeda pasti AB tidak akan sama dengan -BA. Sebagai contoh, matriks
A2X3.B3X2 ≠ B3X2.A2X3. Kenapa? karena A2X3.B3X2 = C2X2 sedangkan B3X2.A2X3 = C3X3. Jadi
melihat ordonya saja sudah jelas tidak mungkin sama.
o Kedua matriks memiliki komponen yang sama dengan komponen positif pada
baris pertama dan komponen negatif pada baris kedua.
Misalnya matriks A dan B adalah :
Pembuktian :
(A+B)2
= A2
+ B2

47. 10. Berikan dua matriks yang memenuhi persamaan A2
- B2
= (A - B)(A + B)
Pembahasan :
A2
- B2
= (A - B)(A + B)
A2
- B2
= A2
+ AB - BA - B2
---> ingat bahwa pada matriks belum tentu AB = BA
A2
- B2
- A2
+ B2
= AB - BA
0 = AB- BA
AB = BA
Beberapa syarat agar AB = BA antara lain:
o Kedua matriks harus matriks persegi misal 2x2, 3x3 dan lain sebagainya. Kedua
matriks harus memiliki ordo sama karena jika ordo berbeda pasti AB tidak akan
sama dengan BA. Sebagai contoh, matriks A2X3.B3X2 ≠ B3X2.A2X3. Kenapa? karena
A2X3.B3X2 = C2X2 sedangkan B3X2.A2X3= C3X3. Jadi melihat ordonya saja sudah jelas tidak
mungkin sama.
o Masing-masing matriks memiliki komponen yang sama di semua sel karena jika
matriks mengandung komponen yang berbeda, saat dibalik maka hasilnya akan
berbeda.
Misal matriks A dan B adalah sebagai berikut :

48. Berdasarkan prinsip kesamaan matriks, maka diperoleh :
ak + bm = ka + lc
al + an = kb + ld
ak + dm = ma + nc
al + dn = mb + nd
untuk tujuan praktis, maka dapat dibuat a = b = c = d dan k = l = m = n.
Salah satu alternatifyangdapat memenuhi persyaratanAB = BA adalah matriks
persegi ordo 2x2 dengan komponen matriks sama di semua sel. misalnya
seperti berikut :
Pembuktian :
A2
- B2
= (A - B)(A + B)
Matriks Identitas (I)
Matriks identitas (I)adalah matriks yang nilai-nilai elemen pada diagonal utama selalu 1.

49. Matriks Transpose(At
)
Matriks transpose adalah matriks yang mengalami pertukaran elemen dari baris menjadi kolom dan
sebaliknya. Contoh:
maka matriks transposenya (At) adalah
Operasiperhitungan pada matriks
Kesamaan 2 matriks
2 matriks dikatakan sama jika ordonya sama dan elemen yang seletak sama.
Contoh:
Tentukan nilai 2x-y+5z!
Jawab:
maka
maka
maka
Penjumlahanmatriks
2 matriks bisa dijumlahkan jika ordonya sama dan penjumlahan dilakukan
dengan cara menjumlahkan elemen yang seletak.

50. Contoh:
Pengurangan matriks
2 matriks bisa dikurangkan jika ordonya sama dan pengurangan dilakukan
dengan cara mengurangkan dari elemen yang seletak.
Contoh:
Perkalianbilangandengan matriks
Contoh:
Perkalianmatriks
2 Matriks dapat dikalikan jika jumlah baris matriks A = jumlah kolom matriks
B.
Penghitungan perkalian matriks:
Misalkan:
dan
maka
Contoh:
Determinan suatu matriks
Matriks ordo2x2
Misalkan:

51. maka Determinan A (ditulis ) adalah:
Matriks ordo3x3
Cara Sarrus
Misalkan:
Jika maka tentukan !
Penghitungan matriks dilakukan dengan cara menambahkan elemen dari
kiri atas ke kanan bawah (mulai dari a → e → i, b → f → g, dan c → d → h)
lalu dikurangi dengan elemen dari kanan atas ke kiri bawah (mulai dari c →
e → g, a → f → h, dan b → d → i) sehingga menjadi:
Contoh:
maka tentukan !
Cara ekspansi baris-kolom
Misalkan:

52. Jika maka tentukan dengan
ekspansi baris pertama!
Matriks Singular
Matriks singular adalah matriks yang nilai determinannya 0.
Contoh:
Jika A matriks singular, tentukan nilai x!
Jawab:
vs
Invers matriks
Invers matriks 2x2
Misalkan:
maka inversnya adalah:
Sifat-sifat invers matriks

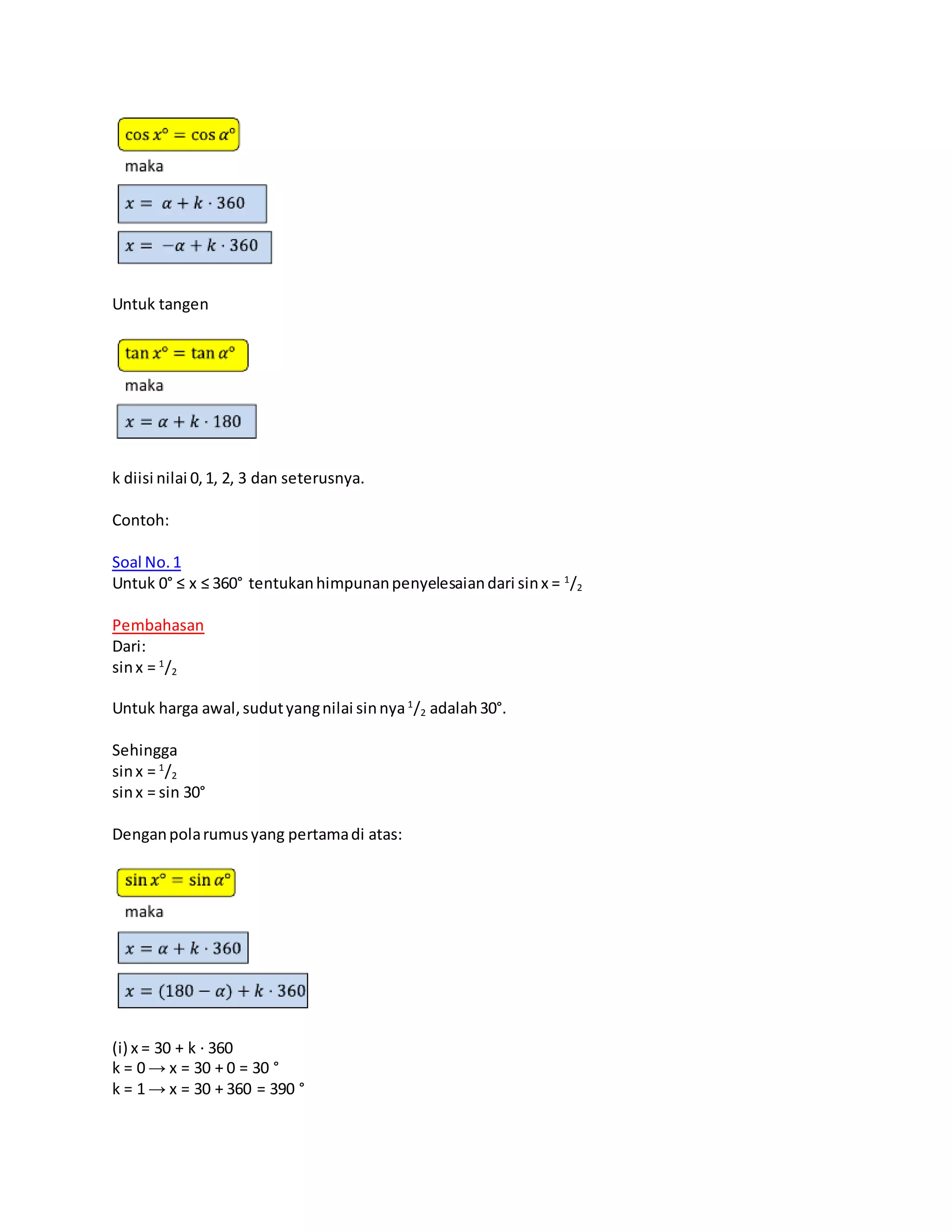
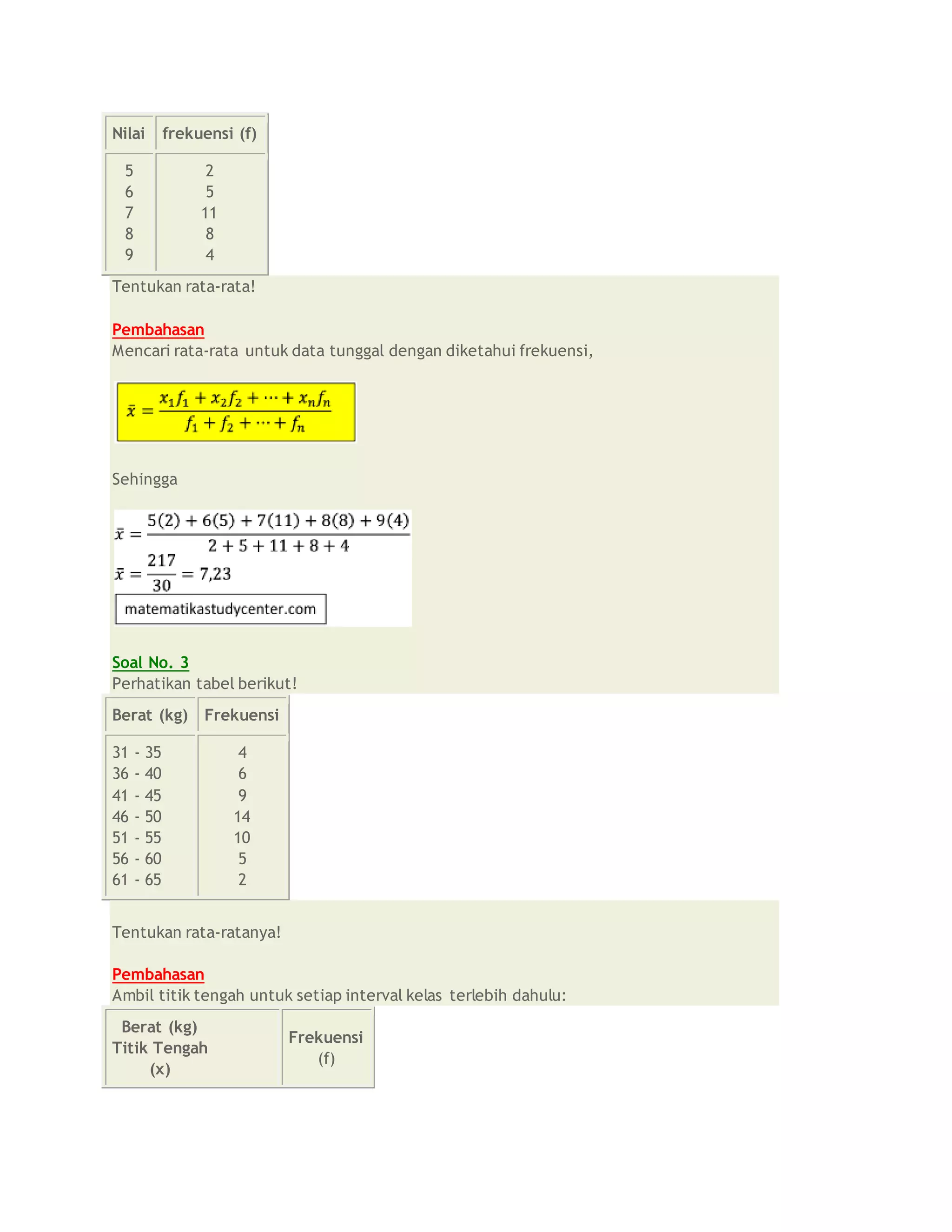
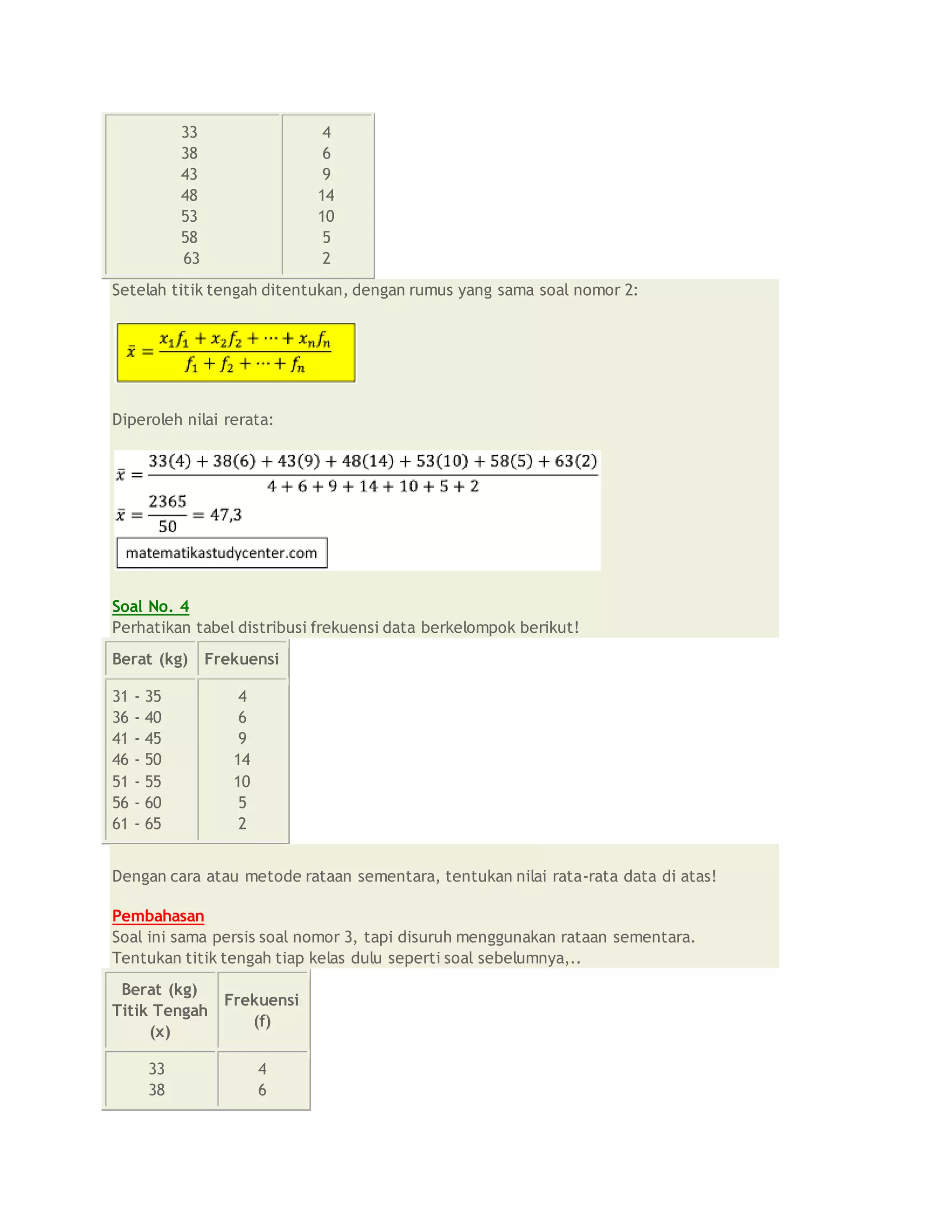
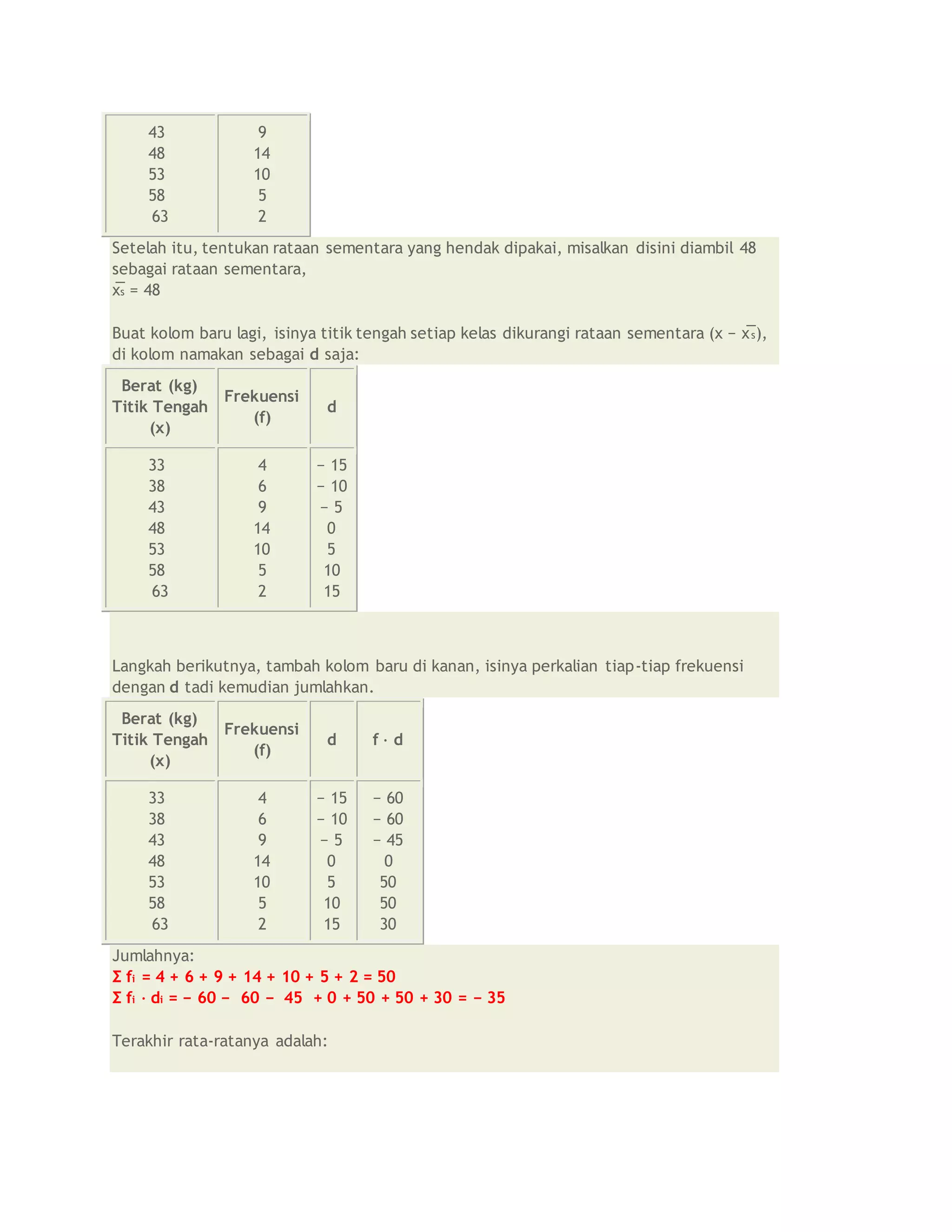
53. Persamaan matriks
Tentukan X matriks dari persamaan:
 Jika diketahui matriks A.X=B
 Jika diketahui
matriks X.A=B
Penjumlahandan penguranganmatriks[sunting | sunting sumber]
Penjumlahan dan pengurangan matriks hanya dapat dilakukan apabila kedua matriks memiliki
ukuran atau tipe yang sama. Elemen-elemen yang dijumlahkan atau dikurangi adalah elemen yang
posisi atau letaknya sama.
atau dalam representasi dekoratfinya
Perkalianskalar[sunting | sunting sumber]
Matriks dapat dikalikan dengan sebuah skalar.
Contoh perhitungan :

54. PerkalianMatriks[sunting | sunting sumber]
Matriks dapat dikalikan, dengan cara tiap baris dikalikan dengan tiap kolom, lalu
dijumlahkan pada baris yang sama.
Contoh perhitungan :
Konsep Perkalian Matriks

55. Bila,matriks A dan B seperti diberikan di bawah ini,maka A.B adalah sebagai
berikut :
Dari contoh di atas dapat dilihat bahwa ordo hasil kali dua buah matriks
bergantung pada banyak baris matriks pertama dan banyak kolom matriks
kedua.
Amxn . Bnxk = Cmxk
Misal :
A2x3 dikali dengan B3x3 akan menghasilkan matriks C2X3
A3X4 dikali dengan B4x2 akan menghasilkan matriks C3X2
A3X1 dikali dengan B1x3 akan menghasilkan matriks C3X3
A1X3 dikali dengan B3X1 akan menghasilkan matriks C1X1
Kumpulan Soal :
1. Matriks A dan B masing-masing seperti di bawah ini. Tentukan A.B dan B.A

56. Pembahasan :
A2X2 dikali dengan B2X2 akan menghasilkan matriks 2x2.
B2X2 dikali dengan A2X2 akan menghasilkan matriks 2x2.
Dari hasil yang diperoleh dapat kita lihat bahwa AB ≠ BA
2. Matriks P dan Q adalah sebagai berikut :

57. Pembahasan :
P2X3 dikali dengan Q3X3 akan menghasilkan matriks 2x3.
3. Tentukan hasil kali K.M jika K dan M seperti di bawah ini.
Pembahasan :
K3X1 dikalikan dengan M1X3 akan menghasilkan matriiks 3x3

58. 4. Matriks A dan B masing-masing seperti di bawah ini. Tentukan A.B
Pembahasan :
A1X3 dikali dengan B3X1 akan menghasilkan matriks 1x1
5. Tentukan hasil dari A.B :

59. Pembahasan :
A4X3 dikali dengan B3X2 akan menghasilkan matriks ordo 4x2
6. Bila matriks A merupakan matriks 2x2 seperti di bawah ini, maka tentukanlah
A2

60. Pembahasan :
7. Buktikan bahwa A.I = I.A. Dengan matriks A seperti pada soal no 6 dan I matriks
identitas 2x2.
Pembahasan :
8. Tentukan A.B jika A dan B seperti di bawah ini.

61. Pembahasan :
Karena A2X2 dan B2X1 maka hasilnya adalah matriks ordo 2x1 seperti ini.
9. Berikan dua matriks A dan B yang memenuhi persamaan (A+B)2
= A2
+ B2
Pembahasan :
(A+B)2
= A2
+ B2
A2
+ AB + BA + B2
= A2
+ B2
---> ingat bahwa pada matriks belum tentu AB = BA
A2
+ B2
- A2
- B2
+ AB + BA = 0
AB + BA = 0
Untuktujuan praktis,anggaplah AB = 0 dan BA = 0 dengan begitu AB + BA = 0.
Beberapa syarat agar AB = BA = 0 antara lain :
o Kedua matriks merupakan matriks persegi yang memiliki ordo sama karena jika
ordo berbeda pasti AB tidak akan sama dengan -BA. Sebagai contoh, matriks
A2X3.B3X2 ≠ B3X2.A2X3. Kenapa? karena A2X3.B3X2 = C2X2 sedangkan B3X2.A2X3 = C3X3. Jadi
melihat ordonya saja sudah jelas tidak mungkin sama.
o Kedua matriks memiliki komponen yang sama dengan komponen positif pada
baris pertama dan komponen negatif pada baris kedua.
Misalnya matriks A dan B adalah :

62. Pembuktian :
(A+B)2
= A2
+ B2
10. Berikan dua matriks yang memenuhi persamaan A2
- B2
= (A - B)(A + B)
Pembahasan :
A2
- B2
= (A - B)(A + B)
A2
- B2
= A2
+ AB - BA - B2
---> ingat bahwa pada matriks belum tentu AB = BA
A2
- B2
- A2
+ B2
= AB - BA
0 = AB- BA
AB = BA
Beberapa syarat agar AB = BA antara lain:
o Kedua matriks harus matriks persegi misal 2x2, 3x3 dan lain sebagainya. Kedua
matriks harus memiliki ordo sama karena jika ordo berbeda pasti AB tidak akan
sama dengan BA. Sebagai contoh, matriks A2X3.B3X2 ≠ B3X2.A2X3. Kenapa? karena
A2X3.B3X2 = C2X2 sedangkan B3X2.A2X3= C3X3. Jadi melihat ordonya saja sudah jelas tidak
mungkin sama.

63. o Masing-masing matriks memiliki komponen yang sama di semua sel karena jika
matriks mengandung komponen yang berbeda, saat dibalik maka hasilnya akan
berbeda.
Misal matriks A dan B adalah sebagai berikut :
Berdasarkan prinsip kesamaan matriks, maka diperoleh :
ak + bm = ka + lc
al + an = kb + ld
ak + dm = ma + nc
al + dn = mb + nd
untuk tujuan praktis, maka dapat dibuat a = b = c = d dan k = l = m = n.
Salah satu alternatifyangdapat memenuhi persyaratanAB = BA adalah matriks
persegi ordo 2x2 dengan komponen matriks sama di semua sel. misalnya
seperti berikut :
Pembuktian :

64. A2
- B2
= (A - B)(A + B)
Kumpulansoal
JikamatriksA diketahui seperti di bawahini,makadeterminanA adalah...
A. (a+ b)(4a- b)
B. (4a + 4b)(a-b)
C. (4a + 2b)(4a + b)
D. (4a + 4b)(4a - 2b)
E. (4a + b)(4a- 4b)
Pembahasan:
detA = 4a2
- 4b2
= 4 (a2
- b2
)
detA = 4 {(a + b)(a- b)}
detA = (4a + 4b)(a- b) --->opsi B
Matriks P danQ adalahmatriksordo2x2 seperti di bawah.AgardeterminanmatriksPsamadengandua
kali determinanQ,makanilai x yangmemenuhi adalah...
A. x = -6 atau x = -2
B. x = 6 atau x = -2
C. x = -6 atau x = 2
D. x = 3 atau x = 4
E. x = -3 atau x = -4
Pembahasan:

65. detP = 2 detQ
2x2
- 6 = 2 (4x - (-9))
2x2
- 6 = 8x + 18
2x2
- 8x - 24 = 0
x2
- 4x - 12 = 0
(x - 6)(x + 2) = 0
x = 6 atau x = -2 --->opsi B
DeterminanmatriksByangmemenuhi persamaandi bawahini adalah...
A. 3
B. -3
C. 1
D. -1
E. 0
Pembahasan:
MisalkankomponenBadalaha,b,c,dan d sebagai berikut:
Dari persamaandi atas diperoleh:
2a + c = 4
a + 2c = 5 --->a = 5 - 2c --->substitusi ke persamaan2a+ c = 4
2 (5-2c) + c = 4
10 - 4c + c = 4
-3c = -6
c = 2
2a + 2 = 4
2a = 2
a = 1
2b + d = 5
b + 2d = 4 ---> b = 4 - 2d --->substitusi ke persamaan2b+ d = 5
2 (4 - 2d) + d = 5
8 - 4d + d = 5
-3d = -3
d = 1

66. 2b + 1 = 5
2b = 4
b = 2
Jadi komponenmatriksBadalahsebagai berikut:
Maka diperoleh:
detB = ac - bd= 1 - 4 = -3 --->opsi B
Diketahui matriksA danB seperti di bawahini.JikadeterminanmatriksA = -8, makadeterminanmatriks
B adalah...
A. 96
B. -96
C. -64
D. 48
E. -48
Pembahasan:
DeterminanA
detA = (aei + bfg+ cdh) - (ceg+ afh+ bdi) = -8
DeterminanB
detB = (-12aei + (-12bfg) + (-12cdh)) - (-12ceg + (-12afh) + (-12bdi))
detB = -12 { (aei + bfg+ cdh) - (ceg+ afh+ bdi)}
detB = -12 detA
detB = -12 (-8)
detB = 96 --->opsi A

67. Nilai zyang memenuhipersamaandi bawahini adalah...
A. 2
B. -2
C. 4
D. 3
E. -3
Pembahasan:
2z2
- (-6) = 8 - (-z(z-1))
2z2
+ 6 = 8 - (-z2
+ z)
2z2
+ 6 = 8 + z2
- z
z2
+ z - 2 = 0
(z + 2)(z - 1) = 0
z = -2 atau z = 1 ---> opsi B
Hubungandua matriksseperti di bawahini.Nilaiayangmemenuhi persamaantersebutadalah...
A. 8
B. 24
C. 64
D. 81
E. 92
Pembahasan:
2 8
loga - 4a = 4a - (- 2
log6 . 6
log16) --->ingatkembali sifatlogaritma:
a
log b . b
logc = a
logc
2 8
loga = 2
log16 = 4
8
loga = 2
a = 82
a = 64 --->opsi C
BiladeterminanmatriksA adalah4 kali determinanmatriksB,makanilai x adalah...

68. A. 4/3
B. 8/3
C. 10/4
D. 5/3
E. 16/7
Pembahasan:
detA = 4 det B
4x
(16x
) - (-16) = 4 (108 - (-152))
4x
(42x
) + 16 = 4 (260)
43x
= 4(260) - 16
43x
= 4(260) - 4(4)
43x
= 4 (260 - 4)
43x
= 4 (256)
43x
= 4. 44
43x
= 45
3x = 5
x = 5/3 --->opsi D