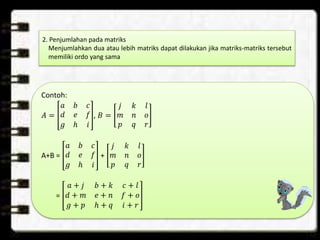
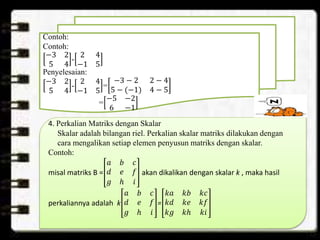
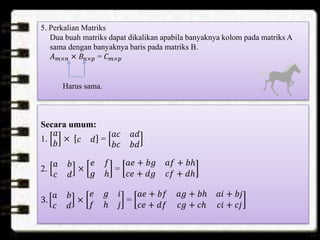
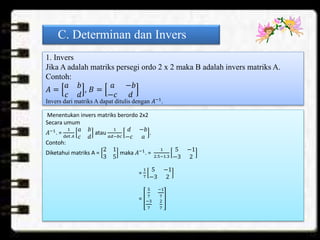
Dokumen tersebut membahas tentang konsep dasar matriks, termasuk pengertian, notasi, ordo, jenis-jenis, dan operasi-operasi matriks seperti penjumlahan, pengurangan, perkalian dengan skalar dan antar matriks, serta determinan dan invers matriks persegi ordo 2x2.

1. MATRIKS
DisusunOleh:
AnggunOktari(18205051)

2. KD : 3.1 Memahami dan menganalisis konsep
dasar operasi matriks dan sifat-sifat
operasi matriks serta menerapkannya
dalam pemecahan masalah.operasi
matriks serta menerapkannya dalam
pemecahan masalah.

3. INDIKATOR:
3.1.1 Mengenal matriks, ordo matriks, baris dan kolom pada
matriks
3.1.2 Mengenal jenis-jenis matrik
3.1.3 Menentukan syarat-syarat penjumlahan dan pengurangan
matriks
3.1.4 Melakukan penjumlahan dan pengurangan matriks
3.1.5 Menentukan syarat-syarat perkalian dua matriks
3.1.6 Melakukan perkalian pada matriks
3.1.7 Menentukan invers suatu matriks
3.1.8 Menentukan determinan suatu matriks persegi ordo 2x2

4. Tujuan Pembelajaran
1. Mengenal matriks, ordo matriks, baris dan kolom pada
matriks
2. Mengenal jenis-jenis matrik
3. Menentukan syarat-syarat penjumlahan dan pengurangan
matriks
4. Melakukan penjumlahan dan pengurangan matriks
5. Melakukan perkalian pada matriks
6. Menentukan syarat-syarat perkalian pada matriks
7. Menentukan invers suatu matriks
8. Menentukan determinan suatu matriks persegi ordo 2 x2

5. PEMBAHASAN
A. Pengertian,Notasi dan Ordo
Matriks
B. Operasi Matriks
C. Determinan dan Invers

6. A. Pengertian, Notasi dan Ordo Matriks
DEFENISI
Matriks adalah susunan-susunan bilangan yang diatur dalam baris dalam
kolom dalam bentuk persegi panjang. Bilangan-bilangan dalam susunan
tersebut disebut elemen.
Matriks dinotasikan dengan huruf besar dan elemen-elemennya akan
dilambangkan dengan huruf kecil.
Contoh:
A=
𝑎11 𝑎12
𝑎21 𝑎22
𝑎31 𝑎32

7. 𝑥
Ordo dari suatu matriks menyatakan banyaknya baris
dan kolom pada matriks itu. Secara umum, jika suatu
matriks A memiliki m baris dan n kolom, maka ordo
matriks A dapat dinyatakan dengan m x n atau ditulis
𝐴 𝑚𝑥𝑛
1. Matriks A adalah matriks ordo 2 × 2
A=
𝑎 𝑏
𝑐 𝑑
, dikatakan matriks ordo 2 × 2 karena matriks A memiliki 2 baris dan 2
kolom.
2. Matriks B adalah matriks ordo 2 × 3
B=
2 4 5
1 3 7
, dikatakan matriks ordo 2 × 3 karena matriks B memiliki 2 baris
dan 3 kolom.
3. Matriks X adalah matriks ordo 3 × 3
X=
𝑎 𝑏 𝑐
𝑑 𝑒 𝑓
𝑔 ℎ 𝑖
, karena matriks X memiliki 3 baris dan 3 kolom maka matriks X
adalah matriks berordo 3 × 3

8. Jenis – jenis Matriks
1. Matriks baris, yaitu
matriks yang terdiri
dari satu baris saja.
Contoh:
A= 1 −2 3
2. Matriks kolom, yaitu
matriks yang terdiri
dari satu kolom saja.
Contoh:
B=
2
−3
−1
3. Matriks persegi, yaitu matriks
yang banyaknya baris sama
dengan banyaknya kolom.
Contoh:
X=
−1 4
2 −5
4. Matriks tegak, yaitu matriks
yang banyak barisnya lebih
banyak dari kolomnya.
Contoh:
C=
−3 3
−4 4
−5 5

9. 5. Matriks datar, yaitu matriks yang banyak
kolomnya lebih banyak dari banyak
barisnya.
Contoh:
J=
2 4 8
−1 3 −5
6. Matriks nol yaitu, matriks yang semua
elemennya adalah nol.
A=
0 0 0
0 0 0
0 0 0
7. Matriks diagonal, yaitu matriks persegi
yang semua elemennya adalah nol kecuali
elemen pada diagonal utamanya.
K=
3 0 0
0 −3 0
0 0 3
8. Matriks segitiga atas, yaitu matriks persegi
yang elemen-elemen diatas diagonalnya
adalah nol.
A=
3 0 0
4 3 0
5 1 −3
9. Matriks segitiga bawah, yaitu matriks persegi yang
elemen-elemen dibawah diagonalnya adalah nol.
K=
3 2 1
0 −3 −2
0 0 3
10. Matriks identitas adalah matriks diagonal yang
semua elemen penyususn pada diagonal utamanya
adalah satu. Biasanya dinyatakan dengan I.
Contoh:
K=
1 0 0
0 1 0
0 0 1
11. Matriks simetri, adalah matriks persegi dengan
elemen pada baris ke-i kolom ke-j sama dengan
elemen pada baris ke-j kolom ke-i.
Contoh:
A=
3 2 1
2 −3 −2
1 0 3

10. B. Operasi Matriks
1. Transpos Matriks
Transpos dari matriks A adalah suatu matriks yang diperoleh dengan cara
menukar setiap elemen baris matriks A dengan elemen kolom matriks
transposnya, maka akan menghasilkan satu matriks baru. Biasanya
transpos matriks dinyatakan dengan 𝐴𝑡
=𝐴 𝑇
=𝐴′
=transpos matriks A
Diberikan sebuah matriks A=
2 −3 7
1 4 −5
Tentukan transposnya.......
Jawab:
𝐴𝑡
=
2 1
−3 4
7 −5

11. 2. Penjumlahan pada matriks
Menjumlahkan dua atau lebih matriks dapat dilakukan jika matriks-matriks tersebut
memiliki ordo yang sama
Contoh:
𝐴 =
𝑎 𝑏 𝑐
𝑑 𝑒 𝑓
𝑔 ℎ 𝑖
, 𝐵 =
𝑗 𝑘 𝑙
𝑚 𝑛 𝑜
𝑝 𝑞 𝑟
A+B =
𝑎 𝑏 𝑐
𝑑 𝑒 𝑓
𝑔 ℎ 𝑖
+
𝑗 𝑘 𝑙
𝑚 𝑛 𝑜
𝑝 𝑞 𝑟
=
𝑎 + 𝑗 𝑏 + 𝑘 𝑐 + 𝑙
𝑑 + 𝑚 𝑒 + 𝑛 𝑓 + 𝑜
𝑔 + 𝑝 ℎ + 𝑞 𝑖 + 𝑟

12. Contoh 2:
Tentukan hasil penjumlahan dari dua buah matriks dibawah ini:
−3 2 6
5 4 6
8 3 5
+
−1 3 −5
8 6 −8
3 2 1
Penyelesaian:
−3 2 6
5 4 6
8 3 5
+
−1 3 −5
8 6 −8
3 2 1
=
−3 + (−1) 2 + 3 6 + (−5)
5 + 8 4 + 6 6 + (−8)
8 + 3 3 + 2 5 + 1
=
−4 5 1
13 10 −2
11 5 6
3. Pengurangan Matriks
Sama dengan penjumlahan pada matriks, pengurangan pada dua atau lebih
matriks dapat dilakukan jika matriks-matriks tersebut memiliki ordo yang
sama.

13. Contoh:
Contoh:
−3 2
5 4
-
2 4
−1 5
Penyelesaian:
−3 2
5 4
-
2 4
−1 5
=
−3 − 2 2 − 4
5 − (−1) 4 − 5
=
−5 −2
6 −1
4. Perkalian Matriks dengan Skalar
Skalar adalah bilangan riel. Perkalian skalar matriks dilakukan dengan
cara mengalikan setiap elemen penyusun matriks dengan skalar.
Contoh:
misal matriks B =
𝑎 𝑏 𝑐
𝑑 𝑒 𝑓
𝑔 ℎ 𝑖
akan dikalikan dengan skalar k , maka hasil
perkaliannya adalah k
𝑎 𝑏 𝑐
𝑑 𝑒 𝑓
𝑔 ℎ 𝑖
=
𝑘𝑎 𝑘𝑏 𝑘𝑐
𝑘𝑑 𝑘𝑒 𝑘𝑓
𝑘𝑔 𝑘ℎ 𝑘𝑖

14. 5. Perkalian Matriks
Dua buah matriks dapat dikalikan apabila banyaknya kolom pada matriks A
sama dengan banyaknya baris pada matriks B.
𝐴 𝑚×𝑛 × 𝐵𝑛×𝑝 = 𝐶 𝑚×𝑝
Harus sama.
Secara umum:
1.
𝑎
𝑏
× 𝑐 𝑑 =
𝑎𝑐 𝑎𝑑
𝑏𝑐 𝑏𝑑
2.
𝑎 𝑏
𝑐 𝑑
×
𝑒 𝑓
𝑔 ℎ
=
𝑎𝑒 + 𝑏𝑔 𝑎𝑓 + 𝑏ℎ
𝑐𝑒 + 𝑑𝑔 𝑐𝑓 + 𝑑ℎ
3.
𝑎 𝑏
𝑐 𝑑
×
𝑒 𝑔 𝑖
𝑓 ℎ 𝑗
=
𝑎𝑒 + 𝑏𝑓 𝑎𝑔 + 𝑏ℎ 𝑎𝑖 + 𝑏𝑗
𝑐𝑒 + 𝑑𝑓 𝑐𝑔 + 𝑐ℎ 𝑐𝑖 + 𝑐𝑗

15. 4.
𝑎 𝑏 𝑐
𝑑 𝑒 𝑓
×
𝑔 𝑗
ℎ 𝑘
𝑖 𝑙
=
𝑎𝑔 + 𝑏ℎ + 𝑐𝑖 𝑎𝑗 + 𝑏𝑘 + 𝑐𝑙
𝑑𝑔 + 𝑒ℎ + 𝑓𝑖 𝑑𝑗 + 𝑒𝑘 + 𝑓𝑙
5.
𝑎 𝑏 𝑐
𝑑 𝑒 𝑓
𝑔 ℎ 𝑖
×
𝑗 𝑚 𝑝
𝑘 𝑛 𝑞
𝑙 𝑜 𝑟
=
𝑎𝑗 + 𝑏𝑘 + 𝑐𝑙 𝑎𝑚 + 𝑏𝑛 + 𝑐0 𝑎𝑝 + 𝑏𝑞 + 𝑐𝑟
𝑑𝑗 + 𝑒𝑘 + 𝑓𝑙 𝑑𝑚 + 𝑒𝑛 + 𝑓𝑜 𝑑𝑝 + 𝑒𝑞 + 𝑓𝑟
𝑔𝑗 + ℎ𝑘 + 𝑖𝑙 𝑔𝑚 + ℎ𝑛 + 𝑖𝑜 𝑔𝑝 + ℎ𝑞 + 𝑖𝑟

16. Contoh soal :
1.
2 5
3 1
×
4 7
6 9
=
2.4 + 5.6 2.7 + 5.9
3.4 + 1.6 3.7 + 1.9
=
38 59
18 30
2.
1 −3 2
−4 5 0
−6 −1 −2
×
1 0 1
2 2 −6
5 8 3
=
1.1 + (−3.2) + 2.5 1.0 + (−3). 2 + 2.8 1.1 + −3 −6 + 2.3
−4.1 + 5.2 + 0.5 −4.0 + 5.2 + 0.8 −4.1 + 5(−6) + 0.3
−6.1 + −1 . 2 + −2 . 5 −6.0 + −1 . 2 + −2 . 8 −6.1 + −1 −6 + (−2). 3
=
1 − 6 + 10 0 − 6 + 10 1 + 18 + 6
−4 + 10 + 0 0 + 10 + 0 −4 − 30 + 0
−6 − 2 − 10 0 − 2 − 16 −6 + 6 − 6
=
5 4 25
6 10 −34
−18 −18 −6

17. C. Determinan dan Invers
1. Invers
Jika A adalah matriks persegi ordo 2 x 2 maka B adalah invers matriks A.
Contoh:
𝐴 =
𝑎 𝑏
𝑐 𝑑
, 𝐵 =
𝑎 −𝑏
−𝑐 𝑑
Invers dari matriks A dapat ditulis dengan 𝐴−1
.
Menentukan invers matriks berordo 2x2
Secara umum
𝐴−1
. =
1
det 𝐴
𝑎 𝑏
𝑐 𝑑
atau
1
𝑎𝑑−𝑏𝑐
𝑑 −𝑏
−𝑐 𝑎
.
Contoh:
Diketahui matriks A =
2 1
3 5
maka 𝐴−1
. =
1
2.5−1.3
5 −1
−3 2
=
1
7
5 −1
−3 2
=
5
7
−1
7
−3
7
2
7

18. 2. Determinan Matriks
Determinan matriks berordo 2x2
Determinan dari matriks berordo 2x2 adalah megurangkan hasil
kali antara elemen-elemen diagonal pertama dengan hasil kali
elemen-elemen diagonal ke dua. Determinan A bisa ditulis dengan
Det A atau 𝐴 .
Contoh:
Misalkan matriks 𝐴 =
𝑎 𝑏
𝑐 𝑑
, determinan matriks A adalah
Det A = 𝐴 =
𝑎 𝑏
𝑐 𝑑
= ad – bc
Contoh lain:
Misalkan matriks 𝐴 =
1 2
3 4
Det A = Det
1 2
3 4
= 1.4 – 2.3
= 4 – 6
= -2

19. EVALUASI
MULAI

20. EVALUASI
1. Diketahui matriks B=
2 −3 7
2 6 −3
, termasuk matriks ordo manakah
matriks B ...
A
B
C
D
Matriks B adalah matriks ordo 2 × 3
Matriks B adalah matriks ordo 2 × 2
Matriks B adalah matriks ordo 3 × 3
Matriks B adalah matriks ordo 3 × 2

21. EVALUASI
2. Diketahui matriks B=
2 −3 7
2 6 −3
, termasuk jenis yang manakah
matriks B . . . .
A
B
C
D
Matriks datar
Matriks tegak
Matriks nol
Matriks persegi

22. EVALUASI
3. Kapan dua buah matriks dapat dijumlahkan. . .
A
B
C
D
Jika memiliki ordo yang sama
Jika memiliki baris yang sama
Jika memiliki kolom yang sama
Boleh kapan saja

23. EVALUASI
4. Berapakah hasil dari pengurangan dua matriks berikut
−3 2
5 4
-
2 4
−1 5
. . . .
A
B
C
D
−1 −2
6 −1
−5 −2
6 −1
−5 −2
6 −9
−1 −2
6 −9

24. EVALUASI
5. Dua matriks dibawah ini dapat dikalikan, kecuali . . . . .
A
B
C
D
2 5
3 1
×
4 7
6 9
−3 2
5 4
×
2 4 2
−1 5 −3
−3 2
5 4
×
0 2
1 −3
−7 −4
1
3
× 2 5

25. EVALUASI
6. Matriks A=
2 5
3 1
dan matriks 𝐵 =
4 7
6 9
, tentukan A X B . . . . .
A
B
C
D
38 21
18 30
38 59
18 30
38 59
19 30
38 21
19 30

26. EVALUASI
7. Jika matriks A =
5 −2
3 −1
dan matriks B=
−2 4
3 −2
, maka
tentukan 𝐴−1 . . . .
A
B
C
D
1 2
3 5
−1 −2
−3 5
−1 −2
−3 −5
5 −3
2 −1

27. EVALUASI
8. Jika matriks A =
5 −2
3 −1
dan matriks B=
−2 4
3 −2
, maka
tentukan det matriks A . . . .
A
B
C
D
2
3
4
1

28. 10. Jika matriks A =
7 −2
3 −1
dan matriks B=
2 1
3 −2
maka
tentukan 𝐴−1
. . . .

29. EVALUASI
Selamat anda sudah mengerjakan soal dengan baik,
silakan klik tombol cek jawaban untuk mengetahui
Hasil jawaban Anda!
Cek jawaban

30. 0
0
0