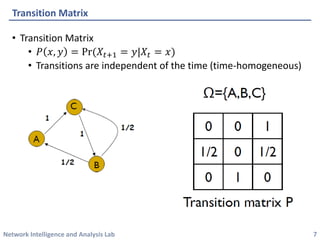
This document discusses Markov chains and their use for algorithmic sampling. It introduces Markov chains and their transition matrices. An example of using a Markov chain for card shuffling is provided. It is shown that an ergodic Markov chain has a unique stationary distribution that it converges to. Coupling techniques are introduced to prove this, and the mixing time is defined as the time it takes to converge to the stationary distribution. An example of using a Markov chain to sample matchings in a graph uniformly is given.

1. Network Intelligence and Analysis Lab
Network Intelligence and Analysis Lab
Markov Chain Basic
2014.07.11
SanghyukChun

2. Network Intelligence and Analysis Lab
•Exact Counting
•#P Complete
•Sampling and Counting
Previous Chapters
2

3. Network Intelligence and Analysis Lab
•Markov Chain Basic
•ErgodicMC has an unique stationary distribution
•Some basic concepts (Coupling, Mixing time)
•Coupling from past
•Coupling detail
•IsingModel
•Bounding Mixing time via Coupling
•Random spanning tree
•Path coupling framework
•MC for k-coloring graph
Remaining Chapters
3
Today!

4. Network Intelligence and Analysis Lab
•Introduce Markov Chain
•Show a potential algorithmic use of Markov Chain for sampling from complex distribution
•Prove that ErgodicMarkov Chain always converge to unique stationary distribution
•Introduce Coupling techniques and Mixing time
In this chapter…
4

5. Network Intelligence and Analysis Lab
•For a finite state space Ω, we say a sequence of random variables (푋푡) on Ωis a Markov chain if the sequence is Markovianin the following sense
•For all t, all 푥0,…,푥푡,푦∈Ω, we require
•Pr푋푡+1=푦푋0=푥0,…,푋푡=푥푡=Pr(푋푡+1=푦|푋푡=푥푡)
•The Markov property: “Memoryless”
Markov Chain
5

6. Network Intelligence and Analysis Lab
•For a finite state space Ω, we say a sequence of random variables (푋푡) on Ωis a Markov chain if the sequence is Markovian
•Let’s Ωdenote the set of shuffling (ex. 푋1=1,2,3,…,52)
•The next shuffling state only depends on previous shuffling state, or 푋푡only depends on 푋푡+1
•Question 1: How can we uniformly shuffle the card?
•Question 2: Can we get fast uniform shuffling algorithm?
Example of Markov Chain (Card Shuffling)
6

7. Network Intelligence and Analysis Lab
•Transition Matrix
•푃푥,푦=Pr(푋푡+1=푦|푋푡=푥)
•Transitions are independent of the time (time-homogeneous)
Transition Matrix
7

8. Network Intelligence and Analysis Lab
•Transition Matrix
•푃푥,푦=Pr(푋푡+1=푦|푋푡=푥)
•Transitions are independent of the time (time-homogeneous)
•The t-step distribution is defined in the natural way
•푃푡푥,푦= 푃푥,푦,푡=1 푧∈Ω푃푥,푧푃푡−1(푧,푦),푡>1
Transition Matrix
8

9. Network Intelligence and Analysis Lab
•A distribution 휋is a stationary distribution if it is invariant with respect to the transition matrix
• forall푦∈Ω,휋푦= 푥∈Ω 휋푥푃(푥,푦)
•Theorem 1
•For a finite ergodicMarkov Chain, there exists a unique stationary distribution 휋
•Proof?
Stationary Distribution
9

10. Network Intelligence and Analysis Lab
•A Markov Chain is ergodicif there exists t such that for all x,푦∈Ω, 푃푥,푦푡>0
•It is possible to go from every state to every state (not necessarily in one move)
•For finite MC following conditions are equivalent to ergodicity
•Irreducible:
•Forall푥,푦∈Ω,thereexists푡=푡푥,푦푠.푡.푃푡푥,푦>0
•Aperiodic:
•Forall푥∈Ω,gcd푡:푃푡푥,푥>0=1
•Since regardless of their initial state, ErgodicMCs eventually reach a unique stationary distribution, EMCs are useful algorithmic tools
ErgodicMarkov Chain
10

11. Network Intelligence and Analysis Lab
•Goal: we have a probability distribution we’d like to generate random sample from
•Solution via MC: If we can design an ergodicMC whose unique stationary distribution is desired distribution, we then run the chain and can get the distribution
•Example: sampling matching
Algorithmic usage of ErgodicMarkov Chains
11

12. Network Intelligence and Analysis Lab
•For a graph 퐺=(푉,퐸), let Ωdenote the set of matching of G
•We define a MC on Ωwhose transitions are as
•Choose an edge e uniformly at random from E
•Let, 푋′= 푋푡∪푒,if푒∉푋푡 푋푡푒,if푒∈푋푡
•If 푋′∈Ω, then set 푋푡+1=푋′with probability ½; otherwise set 푋푡+1=푋푡
•The MC is aperiodic (푃푀,푀≥1/2forall푀∈Ω)
•The MC is irreducible (via empty set) with symmetric transition probabilities
•Symmetric transition matrix has uniform stationary distribution
•Thus, the unique stationary distribution is uniform over all matching of G
Sampling Matching
12

13. Network Intelligence and Analysis Lab
•We will prove the theorem using the coupling technique and coupling Lemma
Proof of Theorem (introduction)
13

14. Network Intelligence and Analysis Lab
•For distribution 휇,휈on a finite setΩ, a distribution ωon Ω×Ωis a coupling if
•In other words, ωis a joint distribution whose marginal distributions are the appropriate distributions
•Variation distance between 휇,휈is defined as
Coupling Technique
14

15. Network Intelligence and Analysis Lab
Coupling Lemma
15

16. Network Intelligence and Analysis Lab
Proof of Lemma (a)
16

17. Network Intelligence and Analysis Lab
•For all 푧∈Ω, let
•휔푧,푧=min{휇푧,휈(푧)}
•푑푇푉=Pr(푋≠푌)
•We need to complete the construction of w in valid way
•For y,푧∈Ω,y≠푧, let
•It is straight forward to verify that w is valid coupling
Proof of Lemma (b)
17

18. Network Intelligence and Analysis Lab
•Consider a pair of Markov chains 푋푡,푌푡on Ωwith transition matrices 푃푋,푃푌respectively
•Typically, MCs are identical in applications (푃푋=푃푌)
•The Markov chainXt′ ,Yt′onΩ×Ωis a Markoviancoupling if
•For such a Markoviancoupling we have variance distance as
•If we choose 푌0as stationary distribution πthen we have
•This shows how can we use coupling to bound the distance from stationary
Couplings for Markov Chain
18

19. Network Intelligence and Analysis Lab
•Create MCs 푋푡,푌푡, where initial 푋0,푌0are arbitrary state on Ω
•Create coupling for there chains in the following way
•From 푋푡,푌푡, choose 푋푡+1according to transition matrix P
•If Yt=푋푡,setYt+1=푋푡+1, otherwise choose Yt+1according to P, independent of the choice for 푋푡
•By ergodicity, there exist 푡∗s.t.forall푥,푦∈Ω,푃푡∗ 푥,푦≥휖>0
•Therefore, for all 푋0,푌0∈Ω
•We can see similarly get step 푡∗→2푡∗
Proof of Theorem(1/4)
19

20. Network Intelligence and Analysis Lab
•Create coupling for there chains in the following way
•From 푋푡,푌푡, choose 푋푡+1according to transition matrix P
•If Yt=푋푡,setYt+1=푋푡+1, otherwise choose Yt+1according to P, independent of the choice for 푋푡
•If once 푋푠=푌푠,wehave푋푠′=푌푠′forall푠′≥푠
•From earlier observation,
Proof of Theorem(2/4)
20

21. Network Intelligence and Analysis Lab
•For integer k > 0,
•Therefore,
•Since Xt=푌푡,impliesXt+1=푌푡+1,forall푡′≥푡, we have
•Note that coupling of MC we defined, defines a coupling of Xt,푌푡. Hence by Coupling Lemma,
•This proves that from any initial points we reach same distribution
Proof of Theorem(3/4)
21
For all 푥,푦∈Ω

22. Network Intelligence and Analysis Lab
•From previous result, we proves there is a limiting distribution σ
•Question: is σa stationary distribution? Or satisfiesforall푦∈Ω,휎푦= 푥∈Ω 휎푥푃(푥,푦)
Proof of Theorem (4/4)
22

23. Network Intelligence and Analysis Lab
•Convergence itself is guaranteed if MC is ErgodicMC
•However, it gives no indication to the convergence rate
•We define the mixing time 휏푚푖푥(휖)as the time until the chain is within variance distance εfrom the worst initial state
•휏푚푖푥휖=maxmin푋0∈Ω{푡:푑푇푉푃푡푋0,∙,휋≤ϵ}
•To get efficient sampling algorithms (e.x. matching chain), we hope that mixing time is polynomial for input size
Markov Chains for Algorithmic Purpose: Mixing Time
23