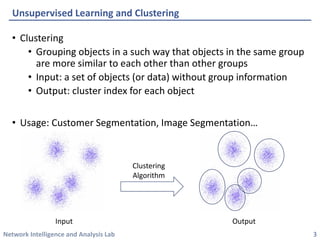
This document discusses clustering methods using the EM algorithm. It begins with an overview of machine learning and unsupervised learning. It then describes clustering, k-means clustering, and how k-means can be formulated as an optimization of a biconvex objective function solved via an iterative EM algorithm. The document goes on to describe mixture models and how the EM algorithm can be used to estimate the parameters of a Gaussian mixture model (GMM) via maximum likelihood.