1. The document proposes an algorithmic framework for large-scale circuit simulation using exponential integrators. It uses exponential Rosenbrock methods and an invert Krylov subspace approach to efficiently compute the matrix exponential-vector product to solve the circuit equations explicitly without needing Newton-Raphson iterations. 2. The framework was shown to accurately simulate benchmark circuits while achieving speedups over traditional approaches. It can handle large-scale, strongly coupled circuits that traditional methods have difficulty with. 3. Future work includes exploring parallelization opportunities to further accelerate the method using multicore/many-core systems and developing additional tools based on the proposed derivatives-based approach.

1. 1. University of California, San Diego
2. Tsinghua University
An Algorithmic Framework of
Large-Scale Circuit Simulation Using
Exponential Integrators
Hao Zhuang1, Wenjian Yu2, Ilgweon Kang1, Xinan
Wang1, and Chung-Kuan Cheng1

2. 2
Outline
• Motivation & Contributions
• Background of time-domain circuit
simulation
• Our algorithmic framework
• Exponential integrators
• Invert Krylov subspace method
• Experimental results
• Conclusions & future directions

3. Motivation
• SPICE
– critical to wide ranges of IC
• Modern IC
– billions of transistors
– complex interconnects
• Requirement:
– new structures e.g., FinFET, 3D
– strong coupled
– post-layout effects
– capability & accuracy
• Simulation runtime
– Long or ∞
3
From Dick Sites, “Datacenter
Computers modern challenges in CPU
design” Google Inc. 2015 & Intel i7
From Synopsys Inc. Issue 3, 2012
Technology Update FinFET: The Promises
and the Challenges

4. • Target of matrix factorization:
conductance matrix 𝐺 ONLY Less expensive
4
Contributions
• Exponential Integration
Stable, Explicit No Newton-Raphson
• Handling tasks (even when traditional schemes
FAIL)
• large-scale, strong coupled, post-layout
A promising framework

5. Basic & BENR as An Example (1)
• Differential Equations
• BE: Backward Euler
5
capacitance
(/inductance)
conductance
(/incidence)
time step
input
nonlinear devices dynamics

6. Basic & BENR as An Example (2)
• NR: Newton-Raphson
• BENR: Backward Euler + Newton-Raphson
iterations
6
Jacobian matrix

7. Basic & BENR as An Example (3)
• NR: Newton-Raphson
• BENR: Backward Euler + Newton-Raphson
iterations
7
Jacobian matrix
capacitance
matrix

8. Matrix Exponential Method
• Our previous attempt [Weng12]
where
8

9. Matrix Exponential Method
• Our previous attempt [Weng12]
where
• It also uses NR
The Jacobian matrix
9
capacitance matrix

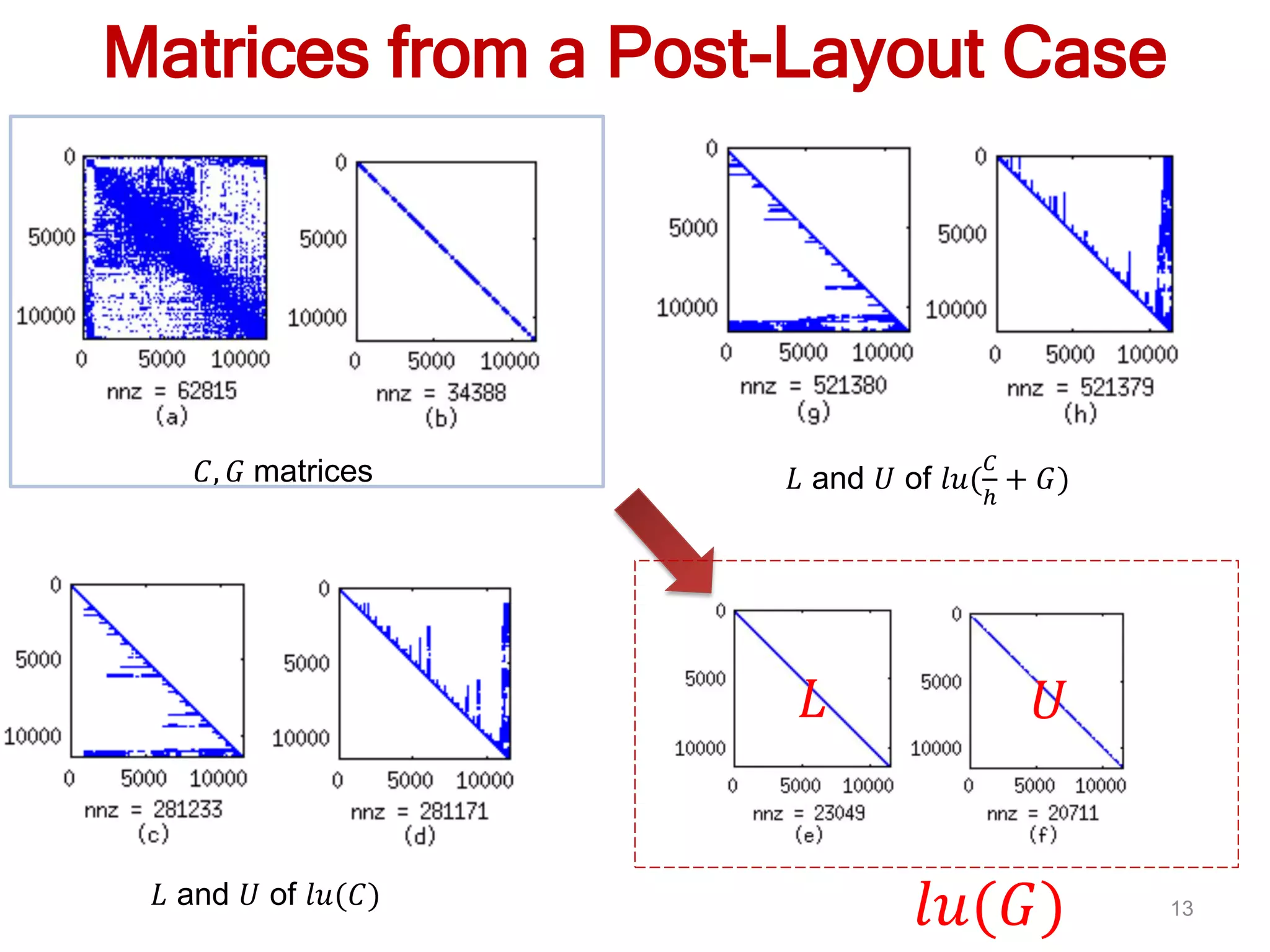
10. 10
𝐶, 𝐺 matrices from FreeCPU [Zhang, Yu TCAD 2013]
nnz: non-zero terms
𝐺𝐶
Matrices from a Post-Layout Case

11. 11𝑙𝑢(𝐶)
𝐶, 𝐺 matrices
𝐺𝐶
𝐿 𝑈
Matrices from a Post-Layout Case

12. 12
𝑙𝑢(
𝐶
𝑕
+ 𝐺)
𝐶, 𝐺 matrices
𝐺𝐶 𝐿 𝑈
Matrices from a Post-Layout Case

13. 13
Matrices from a Post-Layout Case
𝐿 and 𝑈 of 𝑙𝑢(𝐶)
𝐿 and 𝑈 of 𝑙𝑢(
𝐶
ℎ
+ 𝐺)
𝑙𝑢(𝐺)
𝐿 𝑈
𝐶, 𝐺 matrices

14. 14
𝐿 and 𝑈 of 𝑙𝑢(
𝐶
ℎ
+ 𝐺)
𝐿 and 𝑈 of 𝑙𝑢(𝐺)
In this example, 𝑙𝑢(𝐺)
• contains less nnz (~10%)
&
• less complicated nnz
distributions
Matrices from a Post-Layout Case
• Traditional methods are
all challenged by 𝐶,
when 𝐶 is complicated,

15. • Two techniques:
– ER: Exponential Rosenbrock Formulation
– Invert Krylov subspace to compute 𝑒 𝐽 𝑣
• Computational advantages
– Simple matrix factorization target: exploit the
feature of 𝑙𝑢(𝐺)
– Stable explicit method to solve circuit system
15
Our proposed framework

16. ER: Exponential Rosenbrock
Start from
𝑑𝑥 𝑡
𝑑𝑡
= 𝑔(𝑥, 𝑢, 𝑡)
• The next time step solution [Hochbruck, et. al. SIAM09]
𝑥 𝑘+1 = 𝑥 𝑘 + 𝑕 𝑘 𝜙1 𝑕 𝑘 𝐽 𝑘 𝑔(𝑥 𝑘, 𝑢, 𝑡 𝑘) + 𝑕 𝑘
2
𝜙2 𝑕 𝑘 𝐽 𝑘 𝑏k
where 𝐽 𝑘 = 𝜕𝑔/𝜕𝑥, 𝑏 𝑘 = 𝜕𝑔/𝜕𝑡
𝜙1 𝑕 𝑘 𝐽 𝑘 = (𝑒ℎ 𝑘 𝐽 𝑘−𝐼 𝑛)/𝑕 𝑘 𝐽 𝑘
𝜙2 𝑕 𝑘 𝐽 𝑘 = (𝑒ℎ 𝑘 𝐽 𝑘−𝐼 𝑛)/𝑕 𝑘
2
𝐽 𝑘
2
− 𝐼 𝑛/𝑕 𝑘 𝐽 𝑘
16
Exponential Integrators:
Proved to be Stable, Explicit, High-Order Accuracy for ODE

17. ER in Circuit Simulation
Chain rule:
𝑑𝑞 𝑥 𝑡
𝑑𝑥
𝑑𝑥 𝑡
𝑑𝑡
= 𝐵𝑢 𝑡 − 𝑓(𝑥)
where
𝑑𝑞 𝑥 𝑡
𝑑𝑥
= 𝐶 𝑥 𝑡 = 𝐶 𝑘, 𝐽 𝑘 = −𝐶 𝑘
−1
𝐺 𝑘,
𝑔 𝑘 = 𝐽 𝑘 + 𝐶 𝑘
−1
𝐹𝑘 + 𝐵𝑢 𝑡 , 𝑏 𝑘 = 𝐶 𝑘
−1 𝐵𝑢 𝑡 𝑘+1 −𝐵𝑢 𝑡 𝑘
ℎ 𝑘
We have ALL the components to obtain 𝑥 𝑘+1
𝑥 𝑘+1(𝑕 𝑘) = 𝑥 𝑘 + 𝑕 𝑘 𝜙1 𝑕 𝑘 𝐽 𝑘 𝑔(𝑥 𝑘, 𝑢, 𝑡) + 𝑕 𝑘
2
𝜙2 𝑕 𝑘 𝐽 𝑘 𝑏k
17

18. Local Nonlinear Error Control
The local nonlinear error estimator [Caliari09]
𝑒 𝑟𝑟 𝑥 𝑘+1, 𝑥 𝑘 = 𝜙1 𝑕 𝑘 𝐽 𝑘 𝐶 𝑘
−1
Δ𝐹𝑘
where Δ𝐹𝑘 = 𝐹 𝑥 𝑘+1 − 𝐹(𝑥 𝑘)
18
ER-C: ER with Correction Term
Reuse Δ𝐹𝑘 to improve the accuracy by padding
the extra term
𝐷 𝑘 = 𝛾𝑕 𝑘 𝜙2 𝑕 𝑘 𝐽 𝑘 𝐶 𝑘
−1
Δ𝐹𝑘
The further corrected solution is
𝑥 𝑘+1,𝑐 = 𝑥 𝑘+1 − 𝐷 𝑘

19. Krylov Method for MEVP 𝑒 𝐽
𝑣
• 𝑒 𝐽 𝑣: Matrix Exponential and Vector Product
(MEVP) via standard Krylov subspace [Weng12]
𝐾 𝑚 𝐽, 𝑣 ≔ 𝑠𝑝𝑎𝑛 𝑣, 𝐽𝑣, 𝐽2 𝑣, … , 𝐽 𝑚−1 𝑣
– Arnoldi process and Matrix reduction:
𝐽𝑉𝑚 = 𝑉𝑚 𝐻 𝑚 + 𝑕 𝑚+1,𝑚 𝑣 𝑚+1 𝑒 𝑚
T
• MEVP is computed by
𝑒 𝐽 𝑣 ≈ 𝑣 2 𝑉𝑚 𝑒 𝐻 𝑚 𝑒1
• Explicit feature: time stepping only by scaling 𝐻 𝑚
with h,
𝑒ℎ𝐽 𝑣 ≈ 𝑣 2 𝑉𝑚 𝑒ℎ𝐻 𝑚 𝑒1
19

20. 20
Standard Krylov subspace
Im
Re0
“like” these eigenvalues
Eigenvalues of J: small magnitude of Re
Eigenvalues of J: large magnitude of Re
(a) Standard Krylov Basis [Weng12]
𝐾 𝑚 𝐽, 𝑣 ≔ 𝑠𝑝𝑎𝑛 𝑣, 𝐽𝑣, 𝐽2
𝑣, … , 𝐽 𝑚−1
𝑣
spectrum of
𝐽 = −𝑪−𝟏
𝑮

21. 21
Standard Krylov subspace
Im
Re0
• these eigenvalues
defines the major
dynamical behavior
• demand more bases to
characterize
Eigenvalues of J: small magnitude of Re
Eigenvalues of J: large magnitude of Re
(a) Standard Krylov Basis [Weng12]
𝐾 𝑚 𝐽, 𝑣 ≔ 𝑠𝑝𝑎𝑛 𝑣, 𝐽𝑣, 𝐽2
𝑣, … , 𝐽 𝑚−1
𝑣
spectrum of
𝐽 = −𝑪−𝟏
𝑮

22. 22
Im
Re
Im
Re00
Invert Krylov subspace method captures
“important” eigenvalues in the original spectrum
Eigenvalues of J: small magnitude of Re
Eigenvalues of J: large magnitude of Re
Invert Krylov subspace
Invert Krylov Basis [Zhuang, et. al. DAC14]
𝐾 𝑚 𝐽−1, 𝑣 ≔ 𝑠𝑝𝑎𝑛 𝑣, 𝐽−1 𝑣, 𝐽−2 𝑣, … , 𝐽−𝑚+1 𝑣
spectrum of 𝐽−1
spectrum of 𝐽

23. Simple Matrix Fct. Taget
23
Invert Krylov Subspace approach transfers
𝐽 = −𝐶−1
𝐺 𝐽−1
= −𝐺−1
𝐶
At each iteration, we
generate invert
Krylov subspace
𝑉𝑚 = 𝑣1, 𝑣2, ⋯ , 𝑣 𝑚
by solving
−𝑮𝒘 = 𝑪𝒗𝒊−𝟏

24. 24
Overall Framework
ER-C: further
improve the solution
• No Newton-Raphson
• Build upon exponential
integrators
• explicit method for
DAE solver
• adjust error by step
size control

25. Experimental Results
• Implemented in MATLAB2013a & C/C++ (GCC
4.7.3)
– Opensource BSIM3 device model with C
– MATLAB Executable (MEX) external interface
between device evaluation and matrix solvers
• Linux workstation
– Intel CPU i7 3.4GHZ
– 32GB memory.
– Utilize single thread mode.
25

26. Accuracy
26

27. 27
Runtime Performance
• #Dev.: the number of devices.
• nnzC & nnzG: the number of non-zero
elements in linear C and G.
• #step: the number of steps for transient
simulation;
For each time step,
• #NRa: the average NR iterations
• #ma: the average dimension of invert
Krylov subspace
• RT(s): the runtime.
• SP: the runtime speedup Test circuits

28. 28
Conclusions and Future Directions
Accelerate SPICE-level time-domain simulation
• Exponential Integrators
• Stable explicit formulation
• 𝑒 𝐽 𝑣 w/ invert Krylov Subspace & Less expensive
matrix factorizations.
• Handling tasks even when traditional methods fail.
Future directions:
• parallelism, can be accelerated further by
multicore/many-core computing systems.
• many derivatives & tools can be built upon.

29. Thanks and Q&A
29