The document discusses auto-encoding variational Bayes (VAE), detailing its key concepts such as loss function, neural network architecture, and variational inference. It covers the reparameterization trick, stochastic gradient variational Bayes estimators, and provides insights on how these methods enhance posterior inference and scalability for large datasets. It also envelops a variety of applications and theoretical underpinnings that support the implementation of VAE in generative modeling.

1. IS ANYONE INTEREST IN AUTO-ENCODING
VARIATIONAL-BAYES ?
INSTEAD OF “VAE”

2. 1. TBD

3. INTRODUCTION TO VAE (1)
Loss Function
Neural network
architecture
• Variational Inference • Auto encoder
• Mixture Density Network

4. • Characteristics
• Scalable generative model
• Amortized variational inference
• Simple network architecture
• Stochastic gradient descent (Back-propagation)
• Scales to huge datasets
• Inference based on probability graphical model
• Continuous Latent Space
• Data reduction / Data Imputation
• Liable to noisy
INTRODUCTION TO VAE (2)

5. • Paper “Auto-encoding variational bayes”
• “VAE” is a example of experiment results in this paper.
• Introduce the rest of this paper without “VAE”
• Stochastic Gradient Variational Bayes(SGVB) estimator
• Auto-encoding Variational Bayes algorithm
• Reparameterization trick
• Appendix
• Full Variational Bayes
• Marginal Likelihood estimator
• Research trend of VAE
THIS SEMINAR

6. PRELIMINARY

7. • General expression
• A random variable 𝑥 ∈ 𝑋
• A set 𝑦%, ⋯ , 𝑦( of i.i.d observations
𝑝 𝑥, 𝑦%, ⋯ , 𝑦( = 𝑝+ 𝑥 ∏ 𝑝(𝑦.|𝑥)(
.1%
• Given prior 𝑝+ 2 and observations, posterior can be evaluated.
𝑝 𝑥 𝑦%, ⋯ , 𝑦( =
𝑝+(𝑥) ∏ 𝑝 𝑦. 𝑥(
.1%
𝑍
≔
𝑝̅ 𝑥
𝑍
𝑍 ≔ 7 𝑝̅ 𝑥 𝑑𝑥
:
BAYESIAN INFERENCE

8. • Variational Inference
• Approximate the target distribution 𝑝 𝑥 by using a tractable distribution 𝑞(𝑥)
in Q
𝑞∗
= 𝑎𝑟𝑔𝑚𝑖𝑛C∈D 𝐾𝐿(𝑞||𝑝)
• Variational Bound
𝑙𝑜𝑔𝑝 𝑥 = ∫ 𝑙𝑜𝑔𝑝 𝑥 ⋅ 𝑞 𝑧 𝑑𝑧 = 7 𝑙𝑜𝑔
𝑝 𝑥, 𝑧
𝑝 𝑧 𝑥
⋅ 𝑞 𝑧 𝑑
= ∫ 𝑙𝑜𝑔
𝑝 𝑥, 𝑧
𝑞 𝑧
⋅ 𝑞 𝑧 𝑑𝑧 − ∫ 𝑙𝑜𝑔
𝑞 𝑧
𝑝 𝑧 𝑥
⋅ 𝑞 𝑧 𝑑𝑧
VARIATIONAL INFERENCE

9. • Supervised Learning
PROBABILITY GRAPHICAL MODEL
• Unsupervised Learning
(Latent Variable Model)
NX
Z
Φ
NY
Z
Φ
X
e.g) Bayesian Logistic regression e.g) EM algorithm for
Gaussian Mixture Model

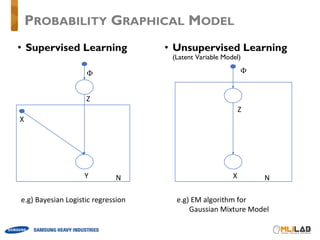
10. • Supervised learning
e.g) Bayesian logistic regression
𝑝 𝑥 𝑤, 𝑦 ⋅ 𝑝 𝑤 ∝ 𝑝 𝑤, 𝑥 𝑦
𝑝 𝑥 𝑤, 𝑦 ∶ ∏ 𝜎 𝑤R
𝑥 ST ⋅ (1 − 𝜎 𝑤R
𝑥 %VST).
W1% à Approximate Gaussian Dist.
• Latent Variable Model
e.g) Gaussian Mixture Model (EM algorithm)
à tractable conditional pdf : 𝑝(𝑧|𝑥)
𝑞 𝑧 ≈ 𝑝 𝑧 𝑥, 𝜃Z[
𝜃∗
= 𝑎𝑟𝑔𝑚𝑎𝑥] ^ 𝑝 𝑧 𝑥, 𝜃Z[
⋅ 𝑙𝑛𝑝(𝑥, 𝑧|𝜃)
_
PROBABILITY GRAPHICAL MODEL

11. • Mean field assumption
• If 𝑝(𝑧|𝑥) is intractable ?
𝑞 𝒛 = a 𝑞W(𝑧W)
W
𝑙𝑛𝑞b
∗
𝑧b = 𝐸Wdb 𝑙𝑛𝑝 𝒙, 𝒛 + 𝑐𝑜𝑛𝑠𝑡
𝑞b
∗
𝑧b =
exp ( 𝐸Wdb[𝑙𝑛𝑝 𝒙, 𝒛 ]
∫ exp ( 𝐸Wdb 𝑙𝑛𝑝 𝒙, 𝒛 𝑑𝑧
• Under specific probabilistic graphical model, approximate distribution can be evaluated by
expectation of 𝐸Wdb[𝑙𝑛𝑝 𝒙, 𝒛 ]
• Depending on each problem, we have to derive the form of 𝐸Wdb[𝑙𝑛𝑝 𝒙, 𝒛 ]
• Through sequential optimization, All of 𝑞b(𝑧b) can be updated in order until converged.
TRADITIONAL VARIATIONAL INFERENCE

12. • VI with Stochastic gradient descent
𝐿 = ∫ 𝑙𝑜𝑔
𝑝 𝑥, 𝑧
𝑞o 𝑧
⋅ 𝑞o 𝑧 𝑑𝑧
𝛻o 𝐿 = ∫ 𝑙𝑛𝑝 𝑥, 𝑧 ⋅ 𝛻o 𝑙𝑛𝑞 𝑧 ⋅ 𝑞 𝑧 𝑑𝑧 = 𝐸2∼C[𝑙𝑛𝑝 𝑥, 𝑧 ⋅ 𝛻o 𝑙𝑛𝑞 𝑧 ]
𝛻o 𝐿 = 𝐸2∼C 𝑙𝑛𝑝 𝑥, 𝑧 ⋅ 𝛻o 𝑙𝑛𝑞 𝑧 ≈
1
𝑛
^ 𝑙𝑛𝑝 𝑥W, 𝑧
W
⋅ 𝛻o 𝑙𝑛𝑞 𝑧
• In order to avoid exact derivation of expectation and sequential optimization, stochastic
gradient descent method was introduced.
• This method only requires 𝑙𝑜𝑔𝑝 𝑥, 𝑧 , 𝑞o 𝑧 and its derivative
• All components can be easily handed
• 𝑙𝑜𝑔𝑝 𝑥, 𝑧 can be derived from probabilistic graphical model
• 𝑞o 𝑧 and 𝛻o 𝑞o 𝑧 are decided by users.
• However, since this estimator has a huge variance, it also requires many samples.
TRADITIONAL VARIATIONAL INFERENCE (2)

13. • Mixture density network
• 𝑝 𝑥 𝑤, 𝑦 ⋅ 𝑝 𝑤 ∝ 𝑝 𝑤, 𝑥 𝑦
𝐸 𝑤 = − ^ ln { ^ 𝜋v 𝑥., 𝑤 𝑁(𝑡.|𝑢v 𝑥., 𝑤 , 𝜎v
y
𝑥., 𝑤 )}
{
v1%
(
.1%
Mixture density network presents that artificial neural network trains hyper-parameters for
learning parameters of distributions
NETWORK FOR LEARNING PARAMETERS
[ Structure of Mixture density Network ] [ Data point and result by Mixture Density Network]

14. • Variational Inference
• It provide the evidence in which mathematical analysis can be conducted
• Before emerging amortized VI, Most researches had a interest in efficient usage of VI using
stochastic gradient descent and improving performance of approximate distribution for
classification model
: Basic example : Bayesian logistic regression.
• Especially, VI with stochastic gradient descent influenced that “Auto-encoding variational bayes”
were published.
• Mixture Density Network
• Mixture Density Network is known to learn parameters of specific distributions using NN
• It is starting point to derive an approach to bayesian neural network
CHAPTER SUMMARY

15. AUTO-ENCODING VARIATIONAL BAYES

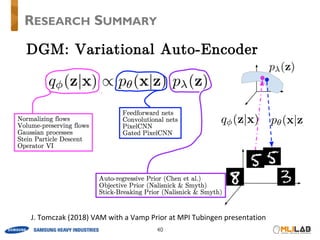
16. • Amortized generative model
• 𝜙 : hyper-parameters in recognition network
• 𝜃 : hyper-parameters in generative network
PROBABILISTIC GRAPHICAL MODEL
NX
Z
𝜙 𝜃
p
𝜇 𝜎
NX
Z
𝜃
𝜙
Generative model
Variational
approximation
[ AEVB algorithm ] [ VAE ]

17. • Traditional Latent variable model
• Intractable : 𝑝(𝑧|𝑥)
• A large data set : Sampling based EM algorithm à Too slow
• This paper has interested in
• Using stochastic gradient descent
• Efficient approximate posterior inference of latent variable 𝑧
• This paper introduce (The reason why this method referred ”Variational”)
• 𝑞o 𝑧 𝑥 : recognition model / approximate posterior distribution to 𝑝] 𝑧 𝑥
• Figure out parameters of approximate distribution
• 𝑝] 𝑥 𝑧 : generative model (defined as graphical model)
• Learning the recognition model parameter 𝜙 with generative model parameter 𝜃
using reparameterization trick
PROBLEMS SCENARIO

18. • Developing variational Bound
∫ 𝑙𝑜𝑔
𝑝 𝑥, 𝑧
𝑞 𝑧
⋅ 𝑞 𝑧 𝑑𝑧 = ∫ 𝑙𝑜𝑔
𝑝 𝑥 𝑧 ⋅ 𝑝 𝑧
𝑞 𝑧
⋅ 𝑞 𝑧 𝑑𝑧
∫ 𝑙𝑜𝑔𝑝 𝑥 𝑧 + 𝑙𝑜𝑔𝑝 𝑧 − 𝑙𝑜𝑔𝑞 𝑧 ⋅ 𝑞 𝑧 𝑑𝑧
= ∫ 𝑙𝑜𝑔𝑝 𝑥 𝑧 ⋅ 𝑞 𝑧 𝑑𝑧 + ∫ 𝑙𝑜𝑔𝑝 𝑧 − 𝑙𝑜𝑔𝑞 𝑧 𝑑𝑧
= ∫ 𝑙𝑜𝑔𝑝 𝑥 𝑧 ⋅ 𝑞 𝑧 𝑑𝑧 − 𝐷{•(𝑞(𝑧)||𝑝(𝑧)
VARIATIONAL BOUND

19. • Reparametrization Trick
• Random variable z à Function of variables (Deterministic)
• Capable of using neural network
• 𝑧 ~ 𝑞 𝑧 𝑥 à 𝑧̅ = 𝑔o(𝑥, ϵ), 𝜖 ~ 𝑝 𝜖
• Assume that 𝑝 𝜖 is defined (𝑝 𝜖 ~ 𝑁(0,1))
• The function 𝑔] is determined depending on 𝑞 𝑧 𝑥
(In subsequent chapter, the forms of function 𝑔] is represented)
• Form of function 𝑔]
• Tractable inverse CDF : similar to finding PDF
• 𝐹 𝑥 = 𝑝, 𝐹V%
𝑝 = 𝑥 𝑢𝑛𝑖𝑞𝑢𝑒 𝑥 / 𝑔o 𝜖, 𝑥 = Fo
V%
𝜖; 𝑥 = 𝑍̅
• Location Scale Model :
• 𝑔o 𝜖, 𝑥 = location + scale ⋅ 𝜖
STOCHASTIC GRADIENT VARIATIONAL BAYES
ESTIMATOR (1)

20. • SGVB Estimator
𝐸Cˆ
(‰|ŠT)
𝑓 𝑧 = 𝐸Œ(•) 𝑓 𝑔o 𝜖, 𝑥W ≈
1
𝐿
^ 𝑓 𝑔o 𝜖[, 𝑥W
W
𝑤ℎ𝑒𝑟𝑒, 𝜖[ ~ 𝑝 𝜖
• 𝑓 𝑧 = 𝑙𝑜𝑔𝑝 𝑥 𝑧 + 𝑞 𝑧 − 𝑝(𝑧)
• 𝐺𝑖𝑣𝑒𝑛 𝑥, 𝜖 𝑠𝑎𝑚𝑝𝑙𝑒𝑑 𝑓𝑟𝑜𝑚 𝑝 𝜖 , 𝑧 ≈ 𝑧̅ = 𝑔o 𝜖, 𝑥W , 𝑓 𝑧 can be evaluated.
• The form of
%
•
∑ 𝑓 𝑔o 𝜖[, 𝑥W
W
• Stochastic gradient method can be introduced w.r.t 𝜙 , 𝜃
(Back propagation)
STOCHASTIC GRADIENT VARIATIONAL BAYES
ESTIMATOR (2)

21. • SGVB Estimator A
𝐿’“(𝜃, 𝜙; 𝑥W
) =
1
𝐿
^ 𝑙𝑜𝑔𝑝 ] 𝑥W
, 𝑧W,[
− 𝑙𝑜𝑔𝑞o(𝑧W,[
|𝑥W
)
[
𝑤ℎ𝑒𝑟𝑒, 𝑔o 𝜖, 𝑥W
, 𝜖[
~ 𝑝 𝜖
• 𝑙𝑜𝑔𝑝 ] 𝑥W
, 𝑧W,[
is defined by probabilistic graphical model
• 𝑙𝑜𝑔𝑞o(𝑧W,[
|𝑥W
) can be determined 𝑔o 𝜖, 𝑥W
, 𝜖[
~ 𝑝 𝜖
• SGVB Estimator B
𝐿”“(𝜃, 𝜙; 𝑥W
) =
1
𝐿
^ 𝑙𝑜𝑔𝑝 ] 𝑥W
|𝑧W,[
− 𝐷{•(𝑞o(𝑧|𝑥W
)||𝑝] 𝑧 )
[
𝑤ℎ𝑒𝑟𝑒, 𝑔o 𝜖, 𝑥W
, 𝜖[
~ 𝑝 𝜖
• 𝐷{•(𝑞o(𝑧|𝑥W
)||𝑝] 𝑧 ) is analytically evaluated (Gaussian Dist.)
• 𝐷{•(𝑞o(𝑧|𝑥W
)||𝑝] 𝑧 ) doesn’t require sample z, only require parameter of approximate dist.
STOCHASTIC GRADIENT VARIATIONAL BAYES
ESTIMATOR (3)

22. 𝑙𝑛𝑝] 𝑋, 𝑍 = ^ 𝑙𝑛𝑝](𝑥W
|𝑧W
)
W
𝑙𝑛𝑞o 𝑍 = ^ 𝑙𝑛𝑞o(𝑧W
)
W
𝑙𝑛𝑝] 𝑍 = ^ 𝑙𝑛𝑝](𝑧W
)
W
AUTO ENCODING VARIATIONAL BAYES
ALGORITHM(1)
NX
Z𝜙 𝜃

23. AUTO ENCODING VARIATIONAL BAYES
ALGORITHM (2)
• AEVB for SGVB estimator
1
𝑀
^ 𝐿’“(𝜃, 𝜙; 𝑥W
)
W
=
1
𝑀
^
1
𝐿
^ 𝑙𝑜𝑔𝑝 ] 𝑥W
, 𝑧W,[
− 𝑙𝑜𝑔𝑞o(𝑧W,[
|𝑥W
)
[
W
1
𝑀
^ 𝐿”“(𝜃, 𝜙; 𝑥W
)
W
=
1
𝑀
^
1
𝐿
^ 𝑙𝑜𝑔𝑝 ] 𝑥W
|𝑧W,[
− 𝐷{•(𝑞o(𝑧|𝑥W
)||𝑝] 𝑧 )
[W

24. • SGVB Estimator
• This estimator was developed to use an approach of neural network for
learning probabilistic latent variable model
• Reparameterization trick is the key point to implement SGVB estimator
• AEVB algorithm
• It can train a neural network using gradient of loss function (SGVB estimator)
w.r.t hyper-parameters in recognition and generative network at once.
• This gradient can be evaluated by back-propagation
CHAPTER SUMMARY

25. VARIATIONAL AUTO ENCODER

26. • Loss function (Bernoulli Case)
• 𝑝 𝑧 ~ 𝑁(0, 𝐼)
• 𝑝] 𝑥|𝑧 ~ 𝑁 𝑢] 𝑧 , 𝜎] 𝑧 𝑜𝑟 𝐵𝑒𝑟𝑛(p] 𝑧 )
• 𝑞o 𝑧|𝑥 ~ 𝑁(𝑢o(𝑥), 𝑑𝑖𝑎𝑔o(𝑥))
• Estimator (Loss function)
𝐿”“(𝜃, 𝜙; 𝑥W
) =
1
𝐿
^ 𝑙𝑜𝑔𝑝 ] 𝑥W
|𝑧W,[
− 𝐷{•(𝑞o(𝑧|𝑥W
)||𝑝] 𝑧 )
[
𝑤ℎ𝑒𝑟𝑒 𝑔o 𝜖, 𝑥W
= 𝑢] 𝑥 + 𝜖 ⋅ 𝜎] 𝑥
𝜖 ~ 𝑁 0, 𝐼 , 𝑙 = 1
• Since 𝑙 = 1, neural network architecture can be similar to “auto-encoder”
FRAMEWORK (1)

27. • Loss function
• 𝑝] 𝑥|𝑧 ~ 𝐵𝑒𝑟𝑛 p] 𝑧
à 𝑙𝑜𝑔𝑝] 𝑥|𝑧 ~ ∑ 𝑥W 𝑙𝑜𝑔pW ]
𝑧W + 1 − 𝑥W 𝑙𝑜𝑔(1 − p](𝑧W))
• 𝐷{•(𝑞o(𝑧|𝑥W)||𝑝] 𝑧 )
• 𝑝 𝑧 ~ 𝑁 0, 𝐼 , 𝑞o 𝑧|𝑥 ~ 𝑁(𝑢o(𝑥), 𝑑𝑖𝑎𝑔o(𝑥))
• 𝐷{•(𝑞o(𝑧|𝑥)| 𝑝] 𝑧 =
%
y
{ 0 − 𝑢o 𝑥 𝐼V% 0 − 𝑢o 𝑥 + 𝑡𝑟𝑎𝑐𝑒(𝐼V% 𝑑𝑖𝑎𝑔o(𝑥)) − 𝑘 + 𝑙𝑛
|™|
|Wš›ˆ 2 |
= ^ 𝑢o 𝑥 (b)
y
− 1 + 𝜎o
y
𝑥 b − 𝑙𝑛𝜎o
y
𝑥 (b)
b
𝑤ℎ𝑒𝑟𝑒 𝑗 = 𝑖𝑛𝑑𝑒𝑥 𝑜𝑓 𝑑𝑖𝑚𝑒𝑛𝑠𝑖𝑜𝑛 𝑜𝑓 𝑙𝑎𝑡𝑒𝑛𝑡 𝑣𝑎𝑟𝑖𝑎𝑏𝑙𝑒 𝑧
FRAMEWORK (2)

28. • Loss Function
∴ ∑ 𝑥W 𝑙𝑜𝑔pW ]
𝑧W + 1 − 𝑥W 𝑙𝑜𝑔(1 − p](𝑧W)) +
^ ^ 𝑢o 𝑥W (b)
y
− 1 + 𝜎o
y
𝑥W b − 𝑙𝑛𝜎o
y
𝑥W (b)
bW
FRAMEWORK (3)

29. • Network Architecture
• Recognition network (like density network)
𝑢o 𝑥W = 𝑤y 𝑡𝑎𝑛ℎ 𝑤% 𝑥W + 𝑏% + 𝑏y
𝜎o 𝑥W = 𝑤Ÿ 𝑡𝑎𝑛ℎ 𝑤 𝑥W + 𝑏 + 𝑏Ÿ
• Generative network
• Bernoulli Case
p] 𝑧W = 𝑓š 𝑤y tanh 𝑤% 𝑧W + 𝑏% + 𝑏y
𝑤ℎ𝑒𝑟𝑒 𝑓š ⋅ : 𝑒𝑙𝑒𝑚𝑒𝑛𝑡 − 𝑤𝑖𝑠𝑒 𝑠𝑖𝑔𝑚𝑜𝑖𝑑 𝑓𝑢𝑛𝑐𝑡𝑖𝑜𝑛
𝜃 = {𝑤%, 𝑏%, 𝑤y, 𝑏y}
• Gaussian Case
𝑢] 𝑧W = 𝑤Ÿ(𝑡𝑎𝑛ℎ 𝑤 𝑧 + 𝑏 + 𝑏Ÿ
𝜎] 𝑧W = 𝑤¥(𝑡𝑎𝑛ℎ 𝑤 𝑧 + 𝑏 + 𝑏¥
𝜃 = {𝑤 , 𝑤Ÿ, 𝑤¥, 𝑏 , 𝑏Ÿ, 𝑏¥}
STRUCTURE OF VAE(1)

30. VAE
• Probabilistic modeling
• All data should be mapped to latent space defined by probability graph model
• Robust against some noises
• Key difference between VAE and general AE

31. • Derivation
• Marginal Likelihood : 𝑝 ] (𝑥)
• Marginal likelihood estimator
1
𝑝](𝑥W)
= ∫
𝑞 𝑧
𝑝] 𝑥W
𝑑𝑧 =
∫ 𝑞 𝑧 ⋅
𝑝] 𝑥W, 𝑧
𝑝] 𝑥W, 𝑧
𝑑𝑧
𝑝] 𝑥W
= ∫
𝑝] 𝑥W, 𝑧
𝑝] 𝑥W
⋅
𝑞 𝑧
𝑝] 𝑥W, 𝑧
𝑑𝑧
= ∫ 𝑝] 𝑧 𝑥W
𝑞 𝑧
𝑝] 𝑥W, 𝑧
𝑑𝑧 ≈
1
𝐿
^
𝑞o(𝑧 [
)
𝑝] 𝑧 𝑝](𝑥W|𝑧 [ )
[
• In VAE, marginal likelihood estimator cannot be evaluated
because it requires 𝑙 > 1
• If it was forced to evaluate the marginal likelihood in VAE, the result is almost same
as loss function, it doesn’t give any special meaning.
MARGINAL LIKELIHOOD ESTIMATOR (1)

32. • Gradient MCMC
• Max Welling and published ”Bayesian learning via stochastic gradient langevin
dynamics (2011), ICML2011”
Δ𝜃¨ =
𝜖¨
2
(∇𝑙𝑜𝑔𝑝 𝜃¨ +
𝑁
𝑛
^ ∇𝑙𝑜𝑔𝑝(𝑥W|𝜃¨
.
W1%
)) + 𝜂¨
𝑤ℎ𝑒𝑟𝑒 𝜂¨~𝑁(0, 𝜖¨)
Update (stochastic gradient descent)
𝜃 = 𝜃¨ + 𝜖¨
¬
⋅ Δ𝜃¨
• In this paper, 𝛻 log 𝑝 𝑧¨ , ∇ log 𝑝(𝑥W|𝑧¨) can be evaluated.
• Under this method, marginal likelihood estimator is established.
MARGINAL LIKELIHOOD ESTIMATOR (2)

33. • Framework
• 𝑝] 𝑧 ~ 𝑁 0, 𝐼 , 𝑤ℎ𝑒𝑟𝑒 𝑧 ∈ 𝑅°, 𝐼 ∈ 𝑅°×°
• 𝑝² 𝜃 ~ 𝑁 0, 𝐼 , 𝑤ℎ𝑒𝑟𝑒 𝜃 ∈ 𝑅³, 𝐼 ∈ 𝑅³×³
• 𝑝] 𝑥|𝑧 ~ 𝑁 𝑢] 𝑧 , 𝜎] 𝑧 𝑜𝑟 𝐵𝑒𝑟𝑛(p] 𝑧 )
• 𝑞o 𝑧|𝑥 ~ 𝑁(𝑢o(𝑥), 𝑑𝑖𝑎𝑔o(𝑥))
FULL VARIATIONAL BAYES
NX
Z
𝜙 𝜃
[ AEVB algorithm ]
𝛼

34. • Variational Bound
𝑙𝑛𝑝] 𝑋 ≈ ∫ 𝑙𝑛𝑃² 𝑋 𝜃 + 𝑙𝑛𝑃² 𝜃 − 𝑙𝑛𝑞o 𝜃 ⋅ 𝑞] 𝜃 𝑑𝜃
=
1
𝐿
^ 𝐸 𝑙𝑛𝑃² 𝑋 𝜃 +
1
2
^{1 + 𝑙𝑛𝜎]
y
¶
[
− 𝜇]
y
¶
[
³
³1%
−𝜎]·
y ([)
}
•
[1%
𝑙𝑛𝑃² 𝑋 𝜃 = ∫ 𝑙𝑜𝑔
𝑝 𝑥, 𝑧
𝑞 𝑧
⋅ 𝑞 𝑧 𝑑𝑧 − ∫ 𝑙𝑜𝑔
𝑞 𝑧
𝑝 𝑧 𝑥
⋅ 𝑞 𝑧 𝑑𝑧
≈
1
𝐾
^(
(
W1%
^ ln𝑝] 𝑥W 𝑧W,b +
1
2
{
v1%
^{1 + 𝑙𝑛𝜎_
y
W,b
v
− 𝜇_
y
W,b
v
°
b1%
−𝜎_T,b
y (v)
})
• In this paper, 𝐿 = 𝐾 = 1 and ln𝑝] 𝑥W 𝑧W,b = 𝑙𝑛𝑝](𝑥|𝑧) , ∀𝑥W
∴ 𝑁 ⋅ 𝑙𝑛𝑝 𝑥 𝑧 +
𝑁
2
⋅ ^{1 + 𝑙𝑛𝜎_
y
W,b
¬
− 𝜇_
y
W,b
¬
°
b1%
−𝜎_T,b
y ¬
} +
1
2
^{1 + 𝑙𝑛𝜎]
y
¶
[
− 𝜇]
y
¶
[
³
³1%
−𝜎]·
y ([)
}
FULL VARIATIONAL BAYES

35. EXPERIMENTAL RESULT

36. STANDARD VAE

37. HIERARCHICAL VAE

38. • Table
EXPERIMENTAL RESULTS

39. WHAT’S NEXT?

40. RESEARCH SUMMARY
J. Tomczak (2018) VAM with a Vamp Prior at MPI Tubingen presentation

41. • Iterative update : 𝒛𝒊 ~ 𝒒 𝝓(𝒛𝒊|𝒙𝒊)
• Based on change of variable
• Objective : minimizing 𝐾𝐿𝐷(𝑞||𝑝)
• Normalizing flow : using tractable determinant of Jacobian
• Stein method : using the RKHS kernel to describe direction for minimizing
KLD
NORMALIZING FLOW / STEIN METHOD

42. VAE WITH VAMPPRIOR
• Main Idea
-. Prior Distribution = Aggregate Posterior Distribution
-. Pseudo inputs
. Users should select learnable pseudo inputs.
. If pseudo inputs are randomly chosen, we couldn’t expect better performance.
-. Expectation for this approach

43. VAE WITH VAMPPRIOR
• Variational Bound

44. VAE WITH VAMPPRIOR
• Experimental Result

45. ANY QUESTIONS?

46. • Kingma and Welling(2013), Auto-encoding Variational Bayes,
ICLR2014
• Bishop(2006), Pattern recognition and Machine learning
• Rezende, Mohamed and Wiestra(2014) Stochastic
Backpropagation and Approximate Inference in Deep Generative
Models, ICML2014
• Liu and Wang(2016), Stein Variational Gradient Descent: A
General Purpose Bayesian Inference Algorithm, NIPS2016
• Tomczak and Welling(2018), VAE with a VampPrior,
AISTAT2018
REFERENCES
J. Tomczak (2018) VAM with a Vamp Prior at MPI Tubingen presentation