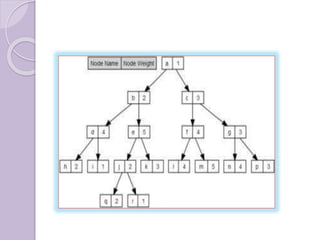
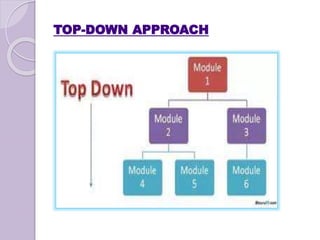
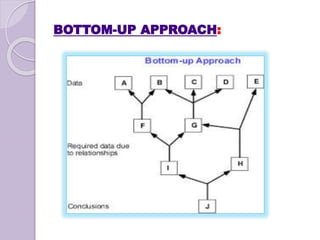
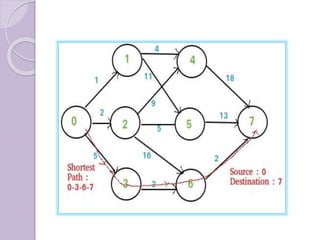
Dynamic programming is a mathematical optimization method and computer programming technique used to solve complex problems by breaking them down into simpler subproblems. It was developed by Richard Bellman in the 1950s and has been applied in many fields. Dynamic programming problems can be solved optimally by breaking them into subproblems with optimal substructures that can be solved recursively. It uses techniques like top-down or bottom-up approaches and storing results of subproblems to solve larger problems efficiently by avoiding recomputing the common subproblems. Multistage graphs are a type of problem well-suited for dynamic programming solutions using techniques like greedy algorithms, Dijkstra's algorithm, or dynamic programming to find shortest paths. Traversal and search algorithms like breadth-

1. Dynamic programming
M.SUJITHA,
II-M.SC (CS&IT),
Nadar Saraswathi College Of Arts and Science,
Theni.

2. • Dynamic programming is both a mathematical
optimization method and a computer programming
method.
• The method was developed by Richard Bellman in 1950s.
• It has found applications in numerous fields,
from Aerospace Engineering to economics.
• It refers to simplifying a complicated problem .
• While some decision problems cannot be taken apart this
way.
• Decisions that span several points in time do often break
apart recursively.

4.  A problem can be solved optimally by breaking it
into sub-problems.
 A recursive form for finding the optimal solutions
to the sub-problems, then it is said to have optimal
substructure.
 The sub-problems can be nested recursively
inside larger problems.
 The dynamic programming methods are
applicable.

5. TOP-DOWN APPROACH

6.  This is the direct fall-out of the recursive
formulation of any problem.
 The solution to any problem can be formulated
recursively using the solution.
 To solve a new sub-problem, first check the table
to see if it is already solved.
 If a solution has been recorded, it may be used
directly, otherwise we solve the sub-problem and
add its solution to the table.

7. BOTTOM-UP APPROACH:

8. • The solution to a problem recursively as in terms
of its sub-problems.
• Solving the sub-problems first and use their
solutions to build-on and arrive at solutions to
bigger sub-problems.
• This is also usually done in a tabular form by
iteratively generating solutions.
EXAMPLE
If already know the values of F41 and F40, we
can directly calculate the value of F42.

9. MULTISTAGE GRAPH

10. • A Multistage graph is a directed graph.
• The nodes can be divided into a set of stages.
• All edges from a stage to next stage .
• There is no edge between vertices of same stage .
• A vertex of current stage to previous stage
• A multistage graph, a source and a destination, we
need to find shortest path from source to
destination.

12. VARIOUS STRATEGIES
• The Brute force method of finding all possible
paths between Source and Destination.
• Dijkstra’s Algorithm has a Single Source shortest
paths.
• This method will find shortest paths from source
to all other nodes which is not required.
• It will take a lot of time and it doesn’t even use the
SPECIAL feature that this MULTI-STAGE graph.

13. Simple Greedy Method
• At each node, choose the shortest outgoing path.
• we apply this approach to the example graph give
above we get the solution as 1 + 4 + 18 = 23.
• But a quick look at the graph will show much
shorter paths available than 23. So the greedy
method fails.
• The best option is Dynamic Programming.
• To find Optimal Sub-structure, Recursive
Equations and Overlapping Sub-problems.

14. BASIC TRAVERSAL AND
SEARCH TECHNIQUES

15. • Traversal of a binary tree involves examining
every node in the tree.
• Search involves visiting nodes in a graph in a
systematic manner, and may or may not result into
a visit to all nodes.
• Different nodes of a graph may be visited,
possibly more than once, during traversal or
search.
• If search results into a visit to all the vertices, it is
called traversal.

16. TECHNIQUES FOR BINARY TREES
 Determine a vertex or a subset of vertices that
satisfy a specified property .
 Possible problem:
 Find all nodes in a binary tree with data value less
than some specified value .
 Solved by systematically examining all the
vertices
 Does searching for a specified item in a binary
search tree result into a traversal.

17. TECHNIQUES FOR GRAPHS
• Reachability problem in graph theory.
• Determine whether a vertex v is reachable from a
vertex u in a graph G = (V,E).
• Whether there exists a path from u to v.
• A more general form:
• Given a vertex u ∈ V , find all vertices vi ∈ V
such that there is a path from u to vi.
• Solved by starting at vertex u and systematically
searching the graph G for vertices reachable from
u.
• Breadth first search and traversal

18.  Explore all vertices adjacent from a starting
vertex.
 A vertex is said to be explored when the
algorithm has visited all the vertices adjacent
from it.
 As a vertex is reached or visited, it becomes a
new unexplored vertex.
 Explore unexplored vertices that are adjacent
to all the explored vertices.
 Breadth-first search operates using a queue to
maintain the list of unexplored vertices.

19. THANKYOU