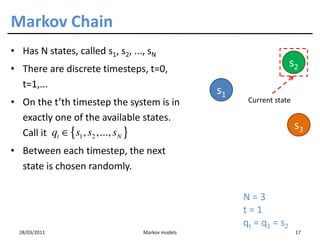
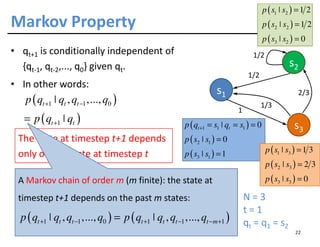
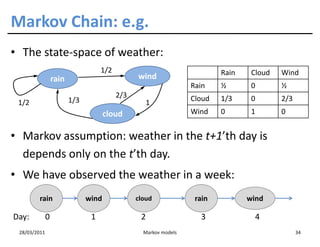
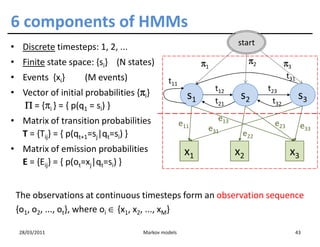
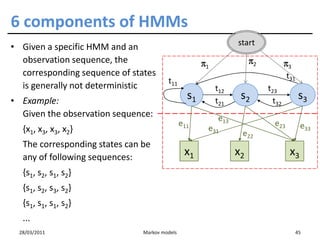
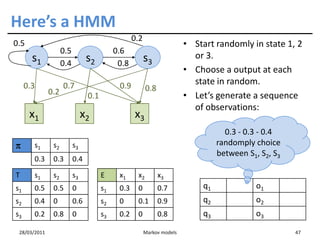
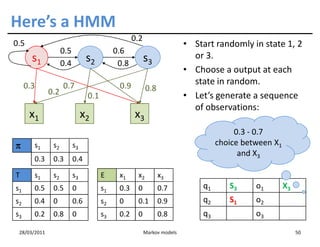
The document discusses Markov models, their origins from Andrei Markov, and applications across various fields such as natural language processing and bioinformatics. It explains concepts like Markov chains, Hidden Markov Models (HMMs), and the transition probabilities between states. The document highlights the importance of context-dependent classification in dealing with dependent random variables.

1. PATTERN RECOGNITION
Markov models
Vu PHAM
phvu@fit.hcmus.edu.vn
Department of Computer Science
March 28th, 2011
28/03/2011 Markov models 1

2. Contents
• Introduction
– Introduction
– Motivation
• Markov Chain
• Hidden Markov Models
• Markov Random Field
28/03/2011 Markov models 2

3. Introduction
• Markov processes are first proposed by
Russian mathematician Andrei Markov
– He used these processes to investigate
Pushkin’s poem.
• Nowadays, Markov property and HMMs are
widely used in many domains:
– Natural Language Processing
– Speech Recognition
– Bioinformatics
– Image/video processing
– ...
28/03/2011 Markov models 3

4. Motivation [0]
• As shown in his paper in 1906, Markov’s original
motivation is purely mathematical:
– Application of The Weak Law of Large Number to dependent
random variables.
• However, we shall not follow this motivation...
28/03/2011 Markov models 4

5. Motivation [1]
• From the viewpoint of classification:
– Context-free classification: Bayes classifier
p (ωi | x ) > p (ω j | x ) ∀j ≠ i
28/03/2011 Markov models 5

6. Motivation [1]
• From the viewpoint of classification:
– Context-free classification: Bayes classifier
p (ωi | x ) > p (ω j | x ) ∀j ≠ i
• Classes are independent.
• Feature vectors are independent.
28/03/2011 Markov models 6

7. Motivation [1]
• From the viewpoint of classification:
– Context-free classification: Bayes classifier
p (ωi | x ) > p (ω j | x ) ∀j ≠ i
– However, there are some applications where various
classes are closely realated:
• POS Tagging, Tracking, Gene boundary recover...
s1 s2 s3 ... sm ...
28/03/2011 Markov models 7

8. Motivation [1]
• Context-dependent classification:
s1 s2 s3 ... sm ...
– s1, s2, ..., sm: sequence of m feature vector
– ω1, ω2,..., ωN: classes in which these vectors are classified: ωi = 1...k.
28/03/2011 Markov models 8

9. Motivation [1]
• Context-dependent classification:
s1 s2 s3 ... sm ...
– s1, s2, ..., sm: sequence of m feature vector
– ω1, ω2,..., ωN: classes in which these vectors are classified: ωi = 1...k.
• To apply Bayes classifier:
– X = s1s2...sm: extened feature vector
– Ωi = ωi1, ωi2,..., ωiN : a classification Nm possible classifications
p ( Ωi | X ) > p ( Ω j | X ) ∀j ≠ i
p ( X | Ωi ) p ( Ωi ) > p ( X | Ω j ) p ( Ω j ) ∀j ≠ i
28/03/2011 Markov models 9

10. Motivation [1]
• Context-dependent classification:
s1 s2 s3 ... sm ...
– s1, s2, ..., sm: sequence of m feature vector
– ω1, ω2,..., ωN: classes in which these vectors are classified: ωi = 1...k.
• To apply Bayes classifier:
– X = s1s2...sm: extened feature vector
– Ωi = ωi1, ωi2,..., ωiN : a classification Nm possible classifications
p ( Ωi | X ) > p ( Ω j | X ) ∀j ≠ i
p ( X | Ωi ) p ( Ωi ) > p ( X | Ω j ) p ( Ω j ) ∀j ≠ i
28/03/2011 Markov models 10

11. Motivation [2]
• From a general view, sometimes we want to evaluate the joint
distribution of a sequence of dependent random variables
28/03/2011 Markov models 11

12. Motivation [2]
• From a general view, sometimes we want to evaluate the joint
distribution of a sequence of dependent random variables
Hôm nay mùng tám tháng ba
Chị em phụ nữ đi ra đi vào...
Hôm nay mùng ... vào ...
q1 q2 q3 qm
28/03/2011 Markov models 12

13. Motivation [2]
• From a general view, sometimes we want to evaluate the joint
distribution of a sequence of dependent random variables
Hôm nay mùng tám tháng ba
Chị em phụ nữ đi ra đi vào...
Hôm nay mùng ... vào ...
q1 q2 q3 qm
• What is p(Hôm nay.... vào) = p(q1=Hôm q2=nay ... qm=vào)?
28/03/2011 Markov models 13

14. Motivation [2]
• From a general view, sometimes we want to evaluate the joint
distribution of a sequence of dependent random variables
Hôm nay mùng tám tháng ba
Chị em phụ nữ đi ra đi vào...
Hôm nay mùng ... vào ...
q1 q2 q3 qm
• What is p(Hôm nay.... vào) = p(q1=Hôm q2=nay ... qm=vào)?
p(s1s2... sm-1 sm)
p(sm|s1s2...sm-1) =
p(s1s2... sm-1)
28/03/2011 Markov models 14

15. Contents
• Introduction
• Markov Chain
• Hidden Markov Models
• Markov Random Field
28/03/2011 Markov models 15

16. Markov Chain
• Has N states, called s1, s2, ..., sN
• There are discrete timesteps, t=0,
s2
t=1,...
s1
• On the t’th timestep the system is in
exactly one of the available states.
s3
Call it qt ∈ {s1 , s2 ,..., sN }
Current state
N=3
t=0
q t = q 0 = s3
28/03/2011 Markov models 16

17. Markov Chain
• Has N states, called s1, s2, ..., sN
• There are discrete timesteps, t=0,
s2
t=1,...
s1
• On the t’th timestep the system is in Current state
exactly one of the available states.
s3
Call it qt ∈ {s1 , s2 ,..., sN }
• Between each timestep, the next
state is chosen randomly.
N=3
t=1
q t = q 1 = s2
28/03/2011 Markov models 17

18. p ( s1 ˚ s2 ) = 1 2
Markov Chain p ( s2 ˚ s2 ) = 1 2
p ( s3 ˚ s2 ) = 0
• Has N states, called s1, s2, ..., sN
• There are discrete timesteps, t=0,
s2
t=1,...
s1
• On the t’th timestep the system is in
exactly one of the available states.
p ( qt +1 = s1 ˚ qt = s1 ) = 0 s3
Call it qt ∈ {s1 , s2 ,..., sN }
p ( s2 ˚ s1 ) = 0
• Between each timestep, the next p ( s3 ˚ s1 ) = 1 p ( s1 ˚ s3 ) = 1 3
state is chosen randomly. p ( s2 ˚ s3 ) = 2 3
p ( s3 ˚ s3 ) = 0
• The current state determines the
probability for the next state. N=3
t=1
q t = q 1 = s2
28/03/2011 Markov models 18

19. p ( s1 ˚ s2 ) = 1 2
Markov Chain p ( s2 ˚ s2 ) = 1 2
p ( s3 ˚ s2 ) = 0
• Has N states, called s1, s2, ..., sN 1/2
• There are discrete timesteps, t=0,
s2
1/2
t=1,...
s1 2/3
• On the t’th timestep the system is in 1/3
1
exactly one of the available states.
p ( qt +1 = s1 ˚ qt = s1 ) = 0 s3
Call it qt ∈ {s1 , s2 ,..., sN }
p ( s2 ˚ s1 ) = 0
• Between each timestep, the next p ( s3 ˚ s1 ) = 1 p ( s1 ˚ s3 ) = 1 3
state is chosen randomly. p ( s2 ˚ s3 ) = 2 3
p ( s3 ˚ s3 ) = 0
• The current state determines the
probability for the next state. N=3
– Often notated with arcs between states
t=1
q t = q 1 = s2
28/03/2011 Markov models 19

20. p ( s1 ˚ s2 ) = 1 2
Markov Property p ( s2 ˚ s2 ) = 1 2
p ( s3 ˚ s2 ) = 0
• qt+1 is conditionally independent of 1/2
{qt-1, qt-2,..., q0} given qt. s2
1/2
• In other words:
s1 2/3
p ( qt +1 ˚ qt , qt −1 ,..., q0 ) 1/3
1
= p ( qt +1 ˚ qt ) p ( qt +1 = s1 ˚ qt = s1 ) = 0 s3
p ( s2 ˚ s1 ) = 0
p ( s3 ˚ s1 ) = 1 p ( s1 ˚ s3 ) = 1 3
p ( s2 ˚ s3 ) = 2 3
p ( s3 ˚ s3 ) = 0
N=3
t=1
q t = q 1 = s2
28/03/2011 Markov models 20

21. p ( s1 ˚ s2 ) = 1 2
Markov Property p ( s2 ˚ s2 ) = 1 2
p ( s3 ˚ s2 ) = 0
• qt+1 is conditionally independent of 1/2
{qt-1, qt-2,..., q0} given qt. s2
1/2
• In other words:
s1 2/3
p ( qt +1 ˚ qt , qt −1 ,..., q0 ) 1/3
1
= p ( qt +1 ˚ qt ) p ( qt +1 = s1 ˚ qt = s1 ) = 0 s3
The state at timestep t+1 depends p ( s2 ˚ s1 ) = 0
p ( s3 ˚ s1 ) = 1 p ( s1 ˚ s3 ) = 1 3
only on the state at timestep t
p ( s2 ˚ s3 ) = 2 3
p ( s3 ˚ s3 ) = 0
N=3
t=1
q t = q 1 = s2
28/03/2011 Markov models 21

22. p ( s1 ˚ s2 ) = 1 2
Markov Property p ( s2 ˚ s2 ) = 1 2
p ( s3 ˚ s2 ) = 0
• qt+1 is conditionally independent of 1/2
{qt-1, qt-2,..., q0} given qt. s2
1/2
• In other words:
s1 2/3
p ( qt +1 ˚ qt , qt −1 ,..., q0 ) 1/3
1
= p ( qt +1 ˚ qt ) p ( qt +1 = s1 ˚ qt = s1 ) = 0 s3
The state at timestep t+1 depends p ( s2 ˚ s1 ) = 0
p ( s3 ˚ s1 ) = 1 p ( s1 ˚ s3 ) = 1 3
only on the state at timestep t
p ( s2 ˚ s3 ) = 2 3
A Markov chain of order m (m finite): the state at p ( s3 ˚ s3 ) = 0
timestep t+1 depends on the past m states: N=3
t=1
p ( qt +1 ˚ qt , qt −1 ,..., q0 ) = p ( qt +1 ˚ qt , qt −1 ,..., qt − m +1 ) q t = q 1 = s2
28/03/2011 Markov models 22

23. p ( s1 ˚ s2 ) = 1 2
Markov Property p ( s2 ˚ s2 ) = 1 2
p ( s3 ˚ s2 ) = 0
• qt+1 is conditionally independent of 1/2
{qt-1, qt-2,..., q0} given qt. s2
1/2
• In other words:
s1 2/3
p ( qt +1 ˚ qt , qt −1 ,..., q0 ) 1/3
1
= p ( qt +1 ˚ qt ) p ( qt +1 = s1 ˚ qt = s1 ) = 0 s3
The state at timestep t+1 depends p ( s2 ˚ s1 ) = 0
p ( s3 ˚ s1 ) = 1 p ( s1 ˚ s3 ) = 1 3
only on the state at timestep t
p ( s2 ˚ s3 ) = 2 3
• How to represent the joint p ( s3 ˚ s3 ) = 0
distribution of (q0, q1, q2...) using
N=3
graphical models? t=1
q t = q 1 = s2
28/03/2011 Markov models 23

24. p ( s1 ˚ s2 ) = 1 2
Markov Property p ( s2 ˚ s2 ) = 1 2
q0p ( s 3 ˚ s2 ) = 0
• qt+1 is conditionally independent of 1/2
{qt-1, qt-2,..., q0} given qt. s2
1/2
• In other words: q1
s1 1/3
p ( qt +1 ˚ qt , qt −1 ,..., q0 ) 1/3
1
= p ( qt +1 ˚ qt ) p ( qt +1 = s1 ˚ qt = s1 ) = 0
q2 s3
The state at timestep t+1 depends p ( s2 ˚ s1 ) = 0
p ( s3 ˚ s1 ) = 1 p ( s1 ˚ s3 ) = 1 3
only on the state at timestep t
• How to represent the joint q3 p ( s 2 ˚ s3 ) = 2 3
p ( s3 ˚ s3 ) = 0
distribution of (q0, q1, q2...) using
N=3
graphical models? t=1
q t = q 1 = s2
28/03/2011 Markov models 24

25. Markov chain
• So, the chain of {qt} is called Markov chain
q0 q1 q2 q3
28/03/2011 Markov models 25

26. Markov chain
• So, the chain of {qt} is called Markov chain
q0 q1 q2 q3
• Each qt takes value from the countable state-space {s1, s2, s3...}
• Each qt is observed at a discrete timestep t
• {qt} sastifies the Markov property: p ( qt +1 ˚ qt , qt −1 ,..., q0 ) = p ( qt +1 ˚ qt )
28/03/2011 Markov models 26

27. Markov chain
• So, the chain of {qt} is called Markov chain
q0 q1 q2 q3
• Each qt takes value from the countable state-space {s1, s2, s3...}
• Each qt is observed at a discrete timestep t
• {qt} sastifies the Markov property: p ( qt +1 ˚ qt , qt −1 ,..., q0 ) = p ( qt +1 ˚ qt )
• The transition from qt to qt+1 is calculated from the transition
probability matrix
1/2
s1 s2 s3
s2 s1 0 0 1
1/2
s1 s2 ½ ½ 0
2/3
1
1/3 s3 1/3 2/3 0
28/03/2011
s3 Markov models
Transition probabilities
27

28. Markov chain
• So, the chain of {qt} is called Markov chain
q0 q1 q2 q3
• Each qt takes value from the countable state-space {s1, s2, s3...}
• Each qt is observed at a discrete timestep t
• {qt} sastifies the Markov property: p ( qt +1 ˚ qt , qt −1 ,..., q0 ) = p ( qt +1 ˚ qt )
• The transition from qt to qt+1 is calculated from the transition
probability matrix
1/2
s1 s2 s3
s2 s1 0 0 1
1/2
s1 s2 ½ ½ 0
2/3
1
1/3 s3 1/3 2/3 0
28/03/2011
s3 Markov models
Transition probabilities
28

29. Markov Chain – Important property
• In a Markov chain, the joint distribution is
m
p ( q0 , q1 ,..., qm ) = p ( q0 ) ∏ p ( q j | q j −1 )
j =1
28/03/2011 Markov models 29

30. Markov Chain – Important property
• In a Markov chain, the joint distribution is
m
p ( q0 , q1 ,..., qm ) = p ( q0 ) ∏ p ( q j | q j −1 )
j =1
• Why? m
p ( q0 , q1 ,..., qm ) = p ( q0 ) ∏ p ( q j | q j −1 , previous states )
j =1
m
= p ( q0 ) ∏ p ( q j | q j −1 )
j =1
Due to the Markov property
28/03/2011 Markov models 30

31. Markov Chain: e.g.
• The state-space of weather:
rain wind
cloud
28/03/2011 Markov models 31

32. Markov Chain: e.g.
• The state-space of weather:
1/2 Rain Cloud Wind
rain wind
Rain ½ 0 ½
2/3 Cloud 1/3 0 2/3
1/2 1/3 1
cloud Wind 0 1 0
28/03/2011 Markov models 32

33. Markov Chain: e.g.
• The state-space of weather:
1/2 Rain Cloud Wind
rain wind
Rain ½ 0 ½
2/3 Cloud 1/3 0 2/3
1/2 1/3 1
cloud Wind 0 1 0
• Markov assumption: weather in the t+1’th day is
depends only on the t’th day.
28/03/2011 Markov models 33

34. Markov Chain: e.g.
• The state-space of weather:
1/2 Rain Cloud Wind
rain wind
Rain ½ 0 ½
2/3 Cloud 1/3 0 2/3
1/2 1/3 1
cloud Wind 0 1 0
• Markov assumption: weather in the t+1’th day is
depends only on the t’th day.
• We have observed the weather in a week:
rain wind cloud rain wind
Day: 0 1 2 3 4
28/03/2011 Markov models 34

35. Markov Chain: e.g.
• The state-space of weather:
1/2 Rain Cloud Wind
rain wind
Rain ½ 0 ½
2/3 Cloud 1/3 0 2/3
1/2 1/3 1
cloud Wind 0 1 0
• Markov assumption: weather in the t+1’th day is
depends only on the t’th day.
• We have observed the weather in a week: Markov Chain
rain wind cloud rain wind
Day: 0 1 2 3 4
28/03/2011 Markov models 35

36. Contents
• Introduction
• Markov Chain
• Hidden Markov Models
– Independent assumptions
– Formal definition
– Forward algorithm
– Viterbi algorithm
– Baum-Welch algorithm
• Markov Random Field
28/03/2011 Markov models 36

37. Modeling pairs of sequences
• In many applications, we have to model pair of sequences
• Examples:
– POS tagging in Natural Language Processing (assign each word in a
sentence to Noun, Adj, Verb...)
– Speech recognition (map acoustic sequences to sequences of words)
– Computational biology (recover gene boundaries in DNA sequences)
– Video tracking (estimate the underlying model states from the observation
sequences)
– And many others...
28/03/2011 Markov models 37

38. Probabilistic models for sequence pairs
• We have two sequences of random variables:
X1, X2, ..., Xm and S1, S2, ..., Sm
• Intuitively, in a pratical system, each Xi corresponds to an observation
and each Si corresponds to a state that generated the observation.
• Let each Si be in {1, 2, ..., k} and each Xi be in {1, 2, ..., o}
• How do we model the joint distribution:
p ( X 1 = x1 ,..., X m = xm , S1 = s1 ,..., S m = sm )
28/03/2011 Markov models 38

39. Hidden Markov Models (HMMs)
• In HMMs, we assume that
p ( X 1 = x1 ,..., X m = xm , S1 = s1 ,..., Sm = sm )
m m
= p ( S1 = s1 ) ∏ p ( S j = s j ˚ S j −1 = s j −1 ) ∏ p ( X j = x j ˚ S j = s j )
j =2 j =1
• This is often called Independence assumptions in
HMMs
• We are gonna prove it in the next slides
28/03/2011 Markov models 39

40. Independence Assumptions in HMMs [1]
p ( ABC ) = p ( A | BC ) p ( BC ) = p ( A | BC ) p ( B ˚ C ) p ( C )
• By the chain rule, the following equality is exact:
p ( X 1 = x1 ,..., X m = xm , S1 = s1 ,..., S m = sm )
= p ( S1 = s1 ,..., S m = sm ) ×
p ( X 1 = x1 ,..., X m = xm ˚ S1 = s1 ,..., S m = sm )
• Assumption 1: the state sequence forms a Markov chain
m
p ( S1 = s1 ,..., S m = sm ) = p ( S1 = s1 ) ∏ p ( S j = s j ˚ S j −1 = s j −1 )
j =2
28/03/2011 Markov models 40

41. Independence Assumptions in HMMs [2]
• By the chain rule, the following equality is exact:
p ( X 1 = x1 ,..., X m = xm ˚ S1 = s1 ,..., S m = sm )
m
= ∏ p ( X j = x j ˚ S1 = s1 ,..., Sm = sm , X 1 = x1 ,..., X j −1 = x j −1 )
j =1
• Assumption 2: each observation depends only on the underlying
state
p ( X j = x j ˚ S1 = s1 ,..., Sm = sm , X 1 = x1 ,..., X j −1 = x j −1 )
= p( X j = xj ˚ S j = sj )
• These two assumptions are often called independence
assumptions in HMMs
28/03/2011 Markov models 41

42. The Model form for HMMs
• The model takes the following form:
m m
p ( x1 ,.., xm , s1 ,..., sm ;θ ) = π ( s1 ) ∏ t ( s j ˚ s j −1 ) ∏ e ( x j ˚ s j )
j =2 j =1
• Parameters in the model:
– Initial probabilities π ( s ) for s ∈ {1, 2,..., k }
– Transition probabilities t ( s ˚ s′ ) for s, s ' ∈ {1, 2,..., k }
– Emission probabilities e ( x ˚ s ) for s ∈ {1, 2,..., k }
and x ∈ {1, 2,.., o}
28/03/2011 Markov models 42

43. 6 components of HMMs
start
• Discrete timesteps: 1, 2, ...
• Finite state space: {si} (N states) π1 π2 π3
• Events {xi} (M events) t31
t11
t12 t23
π
• Vector of initial probabilities {πi} s1 s2 s3
t21 t32
Π = {πi } = { p(q1 = si) }
• Matrix of transition probabilities e13
e11 e23 e33
e31
T = {Tij} = { p(qt+1=sj|qt=si) } e22
• Matrix of emission probabilities x1 x2 x3
E = {Eij} = { p(ot=xj|qt=si) }
The observations at continuous timesteps form an observation sequence
{o1, o2, ..., ot}, where oi ∈ {x1, x2, ..., xM}
28/03/2011 Markov models 43

44. 6 components of HMMs
start
• Discrete timesteps: 1, 2, ...
• Finite state space: {si} (N states) π1 π2 π3
• Events {xi} (M events) t31
t11
t12 t23
π
• Vector of initial probabilities {πi} s1 s2 s3
t21 t32
Π = {πi } = { p(q1 = si) }
• Matrix of transition probabilities e13
e11 e23 e33
e31
T = {Tij} = { p(qt+1=sj|qt=si) } e22
• Matrix of emission probabilities x1 x2 x3
E = {Eij} = { p(ot=xj|qt=si) }
Constraints:
The observations at continuous timesteps form an observation sequence
N N M
∑ πi = 1 ∑ ∑
{o1, o2, ..., ot}, where oi ∈ {x1Tij 2=..., xM} Eij = 1
i =1 j =1
,x , 1
j =1
28/03/2011 Markov models 44

45. 6 components of HMMs
start
• Given a specific HMM and an
observation sequence, the π1 π2 π3
corresponding sequence of states t31
t11
is generally not deterministic t12 t23
• Example: s1 t21
s2 t32
s3
Given the observation sequence: e13
e11 e23 e33
{x1, x3, x3, x2} e31
e22
The corresponding states can be
any of following sequences:
x1 x2 x3
{s1, s2, s1, s2}
{s1, s2, s3, s2}
{s1, s1, s1, s2}
...
28/03/2011 Markov models 45

46. Here’s an HMM
0.2
0.5
0.5 0.6
s1 0.4
s2 0.8
s3
0.3 0.7 0.9 0.8
0.2 0.1
x1 x2 x3
T s1 s2 s3 E x1 x2 x3 π s1 s2 s3
s1 0.5 0.5 0 s1 0.3 0 0.7 0.3 0.3 0.4
s2 0.4 0 0.6 s2 0 0.1 0.9
s3 0.2 0.8 0 s3 0.2 0 0.8
28/03/2011 Markov models 46

47. Here’s a HMM
0.2
0.5 • Start randomly in state 1, 2
0.5 0.6
s1 s2 s3 or 3.
0.4 0.8
• Choose a output at each
0.3 0.7 0.9 state in random.
0.2 0.8
0.1 • Let’s generate a sequence
of observations:
x1 x2 x3
0.3 - 0.3 - 0.4
π s1 s2 s3 randomply choice
between S1, S2, S3
0.3 0.3 0.4
T s1 s2 s3 E x1 x2 x3
s1 0.5 0.5 0 s1 0.3 0 0.7 q1 o1
s2 0.4 0 0.6 s2 0 0.1 0.9 q2 o2
s3 0.2 0.8 0 s3 0.2 0 0.8 q3 o3
28/03/2011 Markov models 47

48. Here’s a HMM
0.2
0.5 • Start randomly in state 1, 2
0.5 0.6
s1 s2 s3 or 3.
0.4 0.8
• Choose a output at each
0.3 0.7 0.9 state in random.
0.2 0.8
0.1 • Let’s generate a sequence
of observations:
x1 x2 x3
0.2 - 0.8
π s1 s2 s3 choice between X1
and X3
0.3 0.3 0.4
T s1 s2 s3 E x1 x2 x3
s1 0.5 0.5 0 s1 0.3 0 0.7 q1 S3 o1
s2 0.4 0 0.6 s2 0 0.1 0.9 q2 o2
s3 0.2 0.8 0 s3 0.2 0 0.8 q3 o3
28/03/2011 Markov models 48

49. Here’s a HMM
0.2
0.5 • Start randomly in state 1, 2
0.5 0.6
s1 s2 s3 or 3.
0.4 0.8
• Choose a output at each
0.3 0.7 0.9 state in random.
0.2 0.8
0.1 • Let’s generate a sequence
of observations:
x1 x2 x3
Go to S2 with
π s1 s2 s3 probability 0.8 or
S1 with prob. 0.2
0.3 0.3 0.4
T s1 s2 s3 E x1 x2 x3
s1 0.5 0.5 0 s1 0.3 0 0.7 q1 S3 o1 X3
s2 0.4 0 0.6 s2 0 0.1 0.9 q2 o2
s3 0.2 0.8 0 s3 0.2 0 0.8 q3 o3
28/03/2011 Markov models 49

50. Here’s a HMM
0.2
0.5 • Start randomly in state 1, 2
0.5 0.6
s1 s2 s3 or 3.
0.4 0.8
• Choose a output at each
0.3 0.7 0.9 state in random.
0.2 0.8
0.1 • Let’s generate a sequence
of observations:
x1 x2 x3
0.3 - 0.7
π s1 s2 s3 choice between X1
and X3
0.3 0.3 0.4
T s1 s2 s3 E x1 x2 x3
s1 0.5 0.5 0 s1 0.3 0 0.7 q1 S3 o1 X3
s2 0.4 0 0.6 s2 0 0.1 0.9 q2 S1 o2
s3 0.2 0.8 0 s3 0.2 0 0.8 q3 o3
28/03/2011 Markov models 50

51. Here’s a HMM
0.2
0.5 • Start randomly in state 1, 2
0.5 0.6
s1 s2 s3 or 3.
0.4 0.8
• Choose a output at each
0.3 0.7 0.9 state in random.
0.2 0.8
0.1 • Let’s generate a sequence
of observations:
x1 x2 x3
Go to S2 with
π s1 s2 s3 probability 0.5 or
S1 with prob. 0.5
0.3 0.3 0.4
T s1 s2 s3 E x1 x2 x3
s1 0.5 0.5 0 s1 0.3 0 0.7 q1 S3 o1 X3
s2 0.4 0 0.6 s2 0 0.1 0.9 q2 S1 o2 X1
s3 0.2 0.8 0 s3 0.2 0 0.8 q3 o3
28/03/2011 Markov models 51

52. Here’s a HMM
0.2
0.5 • Start randomly in state 1, 2
0.5 0.6
s1 s2 s3 or 3.
0.4 0.8
• Choose a output at each
0.3 0.7 0.9 state in random.
0.2 0.8
0.1 • Let’s generate a sequence
of observations:
x1 x2 x3
0.3 - 0.7
π s1 s2 s3 choice between X1
and X3
0.3 0.3 0.4
T s1 s2 s3 E x1 x2 x3
s1 0.5 0.5 0 s1 0.3 0 0.7 q1 S3 o1 X3
s2 0.4 0 0.6 s2 0 0.1 0.9 q2 S1 o2 X1
s3 0.2 0.8 0 s3 0.2 0 0.8 q3 S1 o3
28/03/2011 Markov models 52

53. Here’s a HMM
0.2
0.5 • Start randomly in state 1, 2
0.5 0.6
s1 s2 s3 or 3.
0.4 0.8
• Choose a output at each
0.3 0.7 0.9 state in random.
0.2 0.8
0.1 • Let’s generate a sequence
of observations:
x1 x2 x3
We got a sequence
of states and
π s1 s2 s3 corresponding
0.3 0.3 0.4 observations!
T s1 s2 s3 E x1 x2 x3
s1 0.5 0.5 0 s1 0.3 0 0.7 q1 S3 o1 X3
s2 0.4 0 0.6 s2 0 0.1 0.9 q2 S1 o2 X1
s3 0.2 0.8 0 s3 0.2 0 0.8 q3 S1 o3 X3
28/03/2011 Markov models 53

54. Three famous HMM tasks
• Given a HMM Φ = (T, E, π). Three famous HMM tasks are:
• Probability of an observation sequence (state estimation)
– Given: Φ, observation O = {o1, o2,..., ot}
– Goal: p(O|Φ), or equivalently p(st = Si|O)
• Most likely expaination (inference)
– Given: Φ, the observation O = {o1, o2,..., ot}
– Goal: Q* = argmaxQ p(Q|O)
• Learning the HMM
– Given: observation O = {o1, o2,..., ot} and corresponding state sequence
– Goal: estimate parameters of the HMM Φ = (T, E, π)
28/03/2011 Markov models 54

55. Three famous HMM tasks
• Given a HMM Φ = (T, E, π). Three famous HMM tasks are:
• Probability of an observation sequence (state estimation)
– Given: Φ, observation O = {o1, o2,..., ot}
– Goal: p(O|Φ), or equivalently p(st = Si|O) Calculating the probability of
• Most likely expaination (inference) observing the sequence O over
all of possible sequences.
– Given: Φ, the observation O = {o1, o2,..., ot}
– Goal: Q* = argmaxQ p(Q|O)
• Learning the HMM
– Given: observation O = {o1, o2,..., ot} and corresponding state sequence
– Goal: estimate parameters of the HMM Φ = (T, E, π)
28/03/2011 Markov models 55

56. Three famous HMM tasks
• Given a HMM Φ = (T, E, π). Three famous HMM tasks are:
• Probability of an observation sequence (state estimation)
– Given: Φ, observation O = {o1, o2,..., ot}
– Goal: p(O|Φ), or equivalently p(st = Si|O) Calculating the best
• Most likely expaination (inference) corresponding state sequence,
given an observation
– Given: Φ, the observation O = {o1, o2,..., ot}
sequence.
– Goal: Q* = argmaxQ p(Q|O)
• Learning the HMM
– Given: observation O = {o1, o2,..., ot} and corresponding state sequence
– Goal: estimate parameters of the HMM Φ = (T, E, π)
28/03/2011 Markov models 56

57. Three famous HMM tasks
• Given a HMM Φ = (T, E, π). Three famous HMM tasks are:
• Probability of an observation sequence (state estimation)
– Given: Φ, observation O = {o1, o2,..., ot}
Given an (or a set of)
– Goal: p(O|Φ), or equivalently p(st = Si|O) observation sequence and
• Most likely expaination (inference) corresponding state sequence,
– Given: Φ, the observation O = {o1, o2,..., ot} estimate the Transition matrix,
– Goal: Q* = argmaxQ p(Q|O) Emission matrix and initial
probabilities of the HMM
• Learning the HMM
– Given: observation O = {o1, o2,..., ot} and corresponding state sequence
– Goal: estimate parameters of the HMM Φ = (T, E, π)
28/03/2011 Markov models 57

58. Three famous HMM tasks
Problem Algorithm Complexity
State estimation Forward O(TN2)
Calculating: p(O|Φ)
Inference Viterbi decoding O(TN2)
Calculating: Q*= argmaxQp(Q|O)
Learning Baum-Welch (EM) O(TN2)
Calculating: Φ* = argmaxΦp(O|Φ)
T: number of timesteps
N: number of states
28/03/2011 Markov models 58

59. State estimation problem
• Given: Φ = (T, E, π), observation O = {o1, o2,..., ot}
• Goal: What is p(o1o2...ot) ?
• We can do this in a slow, stupid way
– As shown in the next slide...
28/03/2011 Markov models 59

60. Here’s a HMM
0.5 0.2
0.5 0.6 • What is p(O) = p(o1o2o3)
s1 0.4
s2 0.8
s3 = p(o1=X3 ∧ o2=X1 ∧ o3=X3)?
0.3 0.7 0.9 • Slow, stupid way:
0.2 0.8
0.1
p (O ) = ∑ p ( OQ )
x1 x2 x3 Q∈paths of length 3
= ∑
Q∈paths of length 3
Q∈
p (O | Q ) p (Q )
• How to compute p(Q) for an
arbitrary path Q?
• How to compute p(O|Q) for an
arbitrary path Q?
28/03/2011 Markov models 60

61. Here’s a HMM
0.5 0.2
0.5 0.6 • What is p(O) = p(o1o2o3)
s1 0.4
s2 0.8
s3 = p(o1=X3 ∧ o2=X1 ∧ o3=X3)?
0.3 0.7 0.9 • Slow, stupid way:
0.2 0.8
0.1
p (O ) = ∑ p ( OQ )
x1 x2 x3 Q∈paths of length 3
π s1 s2 s3 = ∑
Q∈paths of length 3
Q∈
p (O | Q ) p (Q )
0.3 0.3 0.4
p(Q) = p(q1q2q3) • How to compute p(Q) for an
= p(q1)p(q2|q1)p(q3|q2,q1) (chain) arbitrary path Q?
= p(q1)p(q2|q1)p(q3|q2) (why?) • How to compute p(O|Q) for an
arbitrary path Q?
Example in the case Q=S3S1S1
P(Q) = 0.4 * 0.2 * 0.5 = 0.04
28/03/2011 Markov models 61

62. Here’s a HMM
0.5 0.2
0.5 0.6 • What is p(O) = p(o1o2o3)
s1 0.4
s2 0.8
s3 = p(o1=X3 ∧ o2=X1 ∧ o3=X3)?
0.3 0.7 0.9 • Slow, stupid way:
0.2 0.8
0.1
p (O ) = ∑ p ( OQ )
x1 x2 x3 Q∈paths of length 3
π s1 s2 s3 = ∑
Q∈paths of length 3
Q∈
p (O | Q ) p (Q )
0.3 0.3 0.4
p(O|Q) = p(o1o2o3|q1q2q3) • How to compute p(Q) for an
= p(o1|q1)p(o2|q1)p(o3|q3) (why?) arbitrary path Q?
• How to compute p(O|Q) for an
Example in the case Q=S3S1S1 arbitrary path Q?
P(O|Q) = p(X3|S3)p(X1|S1) p(X3|S1)
=0.8 * 0.3 * 0.7 = 0.168
28/03/2011 Markov models 62

63. Here’s a HMM
0.5 0.2
0.5 0.6 • What is p(O) = p(o1o2o3)
s1 0.4
s2 0.8
s3 = p(o1=X3 ∧ o2=X1 ∧ o3=X3)?
0.3 0.7 0.9 • Slow, stupid way:
0.2 0.8
0.1
p (O ) = ∑ p ( OQ )
x1 x2 x3 Q∈paths of length 3
π s1 s2 s3 = ∑
Q∈paths of length 3
Q∈
p (O | Q ) p (Q )
0.3 0.3 0.4
p(O|Q) = p(o1o2o3|q1q2q3) • How to compute p(Q) for an
p(O) needs 27 p(Q) arbitrary path Q?
= p(o1|q1)p(o2|q1)p(o3|q3) (why?)
computations and 27
• How to compute p(O|Q) for an
p(O|Q) computations.
Example in the case Q=S3S1S1 arbitrary path Q?
P(O|Q) = p(X3|S3)p(Xsequence3has )
What if the
1|S1) p(X |S1
20 observations?
=0.8 * 0.3 * 0.7 = 0.168 So let’s be smarter...
28/03/2011 Markov models 63

64. The Forward algorithm
• Given observation o1o2...oT
• Forward probabilities:
αt(i) = p(o1o2...ot ∧ qt = si | Φ) where 1 ≤ t ≤ T
αt(i) = probability that, in a random trial:
– We’d have seen the first t observations
– We’d have ended up in si as the t’th state visited.
• In our example, what is α2(3) ?
28/03/2011 Markov models 64

65. αt(i): easy to define recursively
α t ( i ) = p ( o1o2 ...ot ∧ qt = si | Φ )
Π = {π i } = { p ( q1 = si )}
α1 ( i ) = p ( o1 ∧ q1 = si )
= p ( q1 = si ) p ( o1 | q1 = si )
{
T = {Tij } = p ( qt +1 = s j | qt = si ) }
= π i Ei ( o1 ) E = {E } = { p ( o = x
ij t j | q = s )}
t i
α t +1 ( i ) = p ( o1o2 ...ot +1 ∧ qt +1 = si )
N
= ∑ p ( o1o2 ...ot ∧ qt = s j ∧ ot +1 ∧ qt +1 = si )
j =1
N
= ∑ p ( ot +1 ∧ qt +1 = si | o1o2 ...ot ∧ qt = s j ) p ( o1o2 ...ot ∧ qt = s j )
j =1
N
= ∑ p ( ot +1 ∧ qt +1 = si | qt = s j ) α t ( j )
j =1
N
= ∑ p ( ot +1 | qt +1 = si ) p ( qt +1 = si | qt = s j ) α t ( j )
j =1
N
= ∑T ji Ei ( ot +1 ) α t ( j )
j =1
28/03/2011 Markov models 65

66. In our example
0.5 0.2
αt ( i ) = p ( o1o2 ...ot ∧ qt = si | Φ ) s1 0.5
s2 0.6
s3
0.4 0.8
α1 ( i ) = Ei ( o1 ) π i
0.3 0.7 0.9
αt +1 ( i ) = ∑Tji Ei ( ot +1 ) αt ( j ) = Ei ( ot +1 ) ∑Tjiαt ( j ) 0.2 0.1
0.8
j j
x1 x2 x3
π s1 s2 s3
0.3 0.3 0.4
We observed: x1x2
α1(1) = 0.3 * 0.3 = 0.09 α2(1) = 0 * (0.09*0 .5+ 0*0.4 + 0.08*0.2) = 0
α1(2) = 0 α2(2) = 0.1 * (0.09*0.5 + 0*0 + 0.08*0.8) = 0.0109
α1(3) = 0.2 * 0.4 = 0.08 α2(3) = 0 * (0.09*0 + 0*0.6 + 0.08*0) = 0
28/03/2011 Markov models 66

67. Forward probabilities - Trellis
N
s4
s3
s2
s1
1 2 3 4 5 6 T
28/03/2011 Markov models 67

68. Forward probabilities - Trellis
N
α1 (4)
s4
α1 (3) α2 (3) α6 (3)
s3
α1 (2) α3 (2) α5 (2)
s2
α1 (1) α4 (1)
s1
1 2 3 4 5 6 T
28/03/2011 Markov models 68

69. Forward probabilities - Trellis
N α1 ( i ) = Ei ( o1 ) π i
α1 (4)
s4
α1 (3) α2 (3)
s3
α1 (2)
s2
α1 (1)
s1
1 2 3 4 5 6 T
28/03/2011 Markov models 69

70. Forward probabilities - Trellis
N αt +1 ( i ) = Ei ( ot +1 ) ∑Tjiαt ( j )
α1 (4) j
s4
α1 (3) α2 (3)
s3
α1 (2)
s2
α1 (1)
s1
1 2 3 4 5 6 T
28/03/2011 Markov models 70

71. Forward probabilities
• So, we can cheaply compute:
αt ( i ) = p ( o1o2 ...ot ∧ qt = si )
• How can we cheaply compute:
p ( o1 o 2 ...o t )
• How can we cheaply compute:
p ( q t = s i | o1 o 2 ...o t )
28/03/2011 Markov models 71

72. Forward probabilities
• So, we can cheaply compute:
αt ( i ) = p ( o1o2 ...ot ∧ qt = si )
• How can we cheaply compute:
p ( o1 o 2 ...o t ) = ∑ α (i )
i
t
• How can we cheaply compute:
αt ( i )
p ( q t = s i | o1 o 2 ...o t ) =
∑α t ( j )
j
Look back the trellis...
28/03/2011 Markov models 72

73. State estimation problem
• State estimation is solved:
N
p ( O | Φ ) = p ( o1o2 … ot ) = ∑ α i ( i )
i =1
• Can we utilize the elegant trellis to solve the Inference
problem?
– Given an observation sequence O, find the best state sequence Q
Q = arg max p ( Q | O )
*
Q
28/03/2011 Markov models 73

74. Inference problem
• Given: Φ = (T, E, π), observation O = {o1, o2,..., ot}
• Goal: Find Q * = arg max p ( Q | O )
Q
= arg max p ( q1q2 … qt | o1o2 … ot )
q1q2 … qt
• Practical problems:
– Speech recognition: Given an utterance (sound), what is
the best sentence (text) that matches the utterance?
– Video tracking s1 s2 s3
– POS Tagging
28/03/2011
x1
Markov models
x2 x3 74

75. Inference problem
• We can do this in a slow, stupid way:
Q * = arg max p ( Q | O )
Q
p (O | Q ) p (Q )
= arg max
Q p (O )
= arg max p ( O | Q ) p ( Q )
Q
= arg max p ( o1o2 … ot | Q ) p ( Q )
Q
• But it’s better if we can find another way to
compute the most probability path (MPP)...
28/03/2011 Markov models 75

76. Efficient MPP computation
• We are going to compute the following variables:
δ t ( i ) = max p ( q1q2 … qt −1 ∧ qt = si ∧ o1o2 …ot )
q1q2 …qt −1
• δt(i) is the probability of the best path of length
t-1 which ends up in si and emits o1...ot.
• Define: mppt(i) = that path
so: δt(i) = p(mppt(i))
28/03/2011 Markov models 76

77. Viterbi algorithm
δ t ( i ) = max p ( q1q2 … qt −1 ∧ qt = si ∧ o1o2 … ot )
q1q2 …qt −1
mppt ( i ) = arg max p ( q1q2 … qt −1 ∧ qt = si ∧ o1o2 …ot )
q1q2 …qt −1
δ1 ( i ) = max p ( q1 = si ∧ o1 )
one choice
= π i Ei ( o1 ) = α1 ( i )
N δ (4)
1
s4
δ 1 (3)
s3 δ 2 (3)
δ 1 (2)
s2
s1
δ 1 (1)
1 2 3 4 5 6 T
28/03/2011 Markov models 77

78. Viterbi algorithm
time t time t + 1
• The most prob path with last two states
s1
sisj is the most path to si, followed by
...
transition si sj.
si sj
• The prob of that path will be:
...
...
δt(i) × p(si sj ∧ ot+1)
= δt(i)TijEj(ot+1)
• So, the previous state at time t is:
i* = arg max δ t ( i ) Tij E j ( ot +1 )
i
28/03/2011 Markov models 78

79. Viterbi algorithm
• Summary: δ t +1 ( j ) = δ t ( i* ) Tij E j ( ot +1 ) δ1 ( i ) = π i Ei ( o1 ) = α1 ( i )
mppt +1 ( j ) = mppt i* s j ( )
i* = arg max δ t ( i ) Tij E j ( ot +1 )
i
N δ (4)
1
s4
δ 1 (3)
s3 δ 2 (3)
δ 1 (2)
s2
s1
δ 1 (1)
1 2 3 4 5 6 T
28/03/2011 Markov models 79

80. What’s Viterbi used for?
• Speech Recognition
Chong, Jike and Yi, Youngmin and Faria, Arlo and Satish, Nadathur Rajagopalan and Keutzer, Kurt, “Data-Parallel Large Vocabulary
Continuous Speech Recognition on Graphics Processors”, EECS Department, University of California, Berkeley, 2008.
28/03/2011 Markov models 80

81. Training HMMs
• Given: large sequence of observation o1o2...oT
and number of states N.
• Goal: Estimation of parameters Φ = 〈T, E, π〉
• That is, how to design an HMM.
• We will infer the model from a large amount of
data o1o2...oT with a big “T”.
28/03/2011 Markov models 81

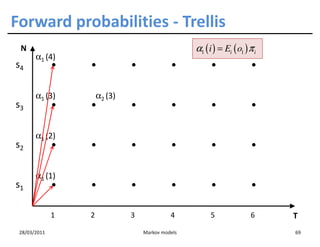
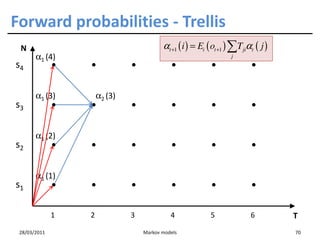
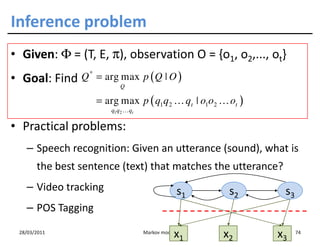
82. Training HMMs
• Remember, we have just computed
p(o1o2...oT | Φ)
• Now, we have some observations and we want to inference Φ
from them.
• So, we could use:
– MAX LIKELIHOOD: Φ = arg max p ( o1 … oT | Φ )
Φ
– BAYES:
Compute p ( Φ | o1 … oT )
then take E [ Φ ] or max p ( Φ | o1 … oT )
Φ
28/03/2011 Markov models 82

83. Max likelihood for HMMs
• Forward probability: the probability of producing o1...ot while
ending up in state si
α1 ( i ) = Ei ( o1 ) π i
αt ( i ) = p ( o1o2 ...ot ∧ qt = si )
α t +1 ( i ) = Ei ( ot +1 ) ∑ T jiα t ( j )
j
• Backward probability: the probability of producing ot+1...oT given
that at time t, we are at state si
βt ( i ) = p ( ot +1ot +2 ...oT | qt = si )
28/03/2011 Markov models 83

84. Max likelihood for HMMs - Backward
• Backward probability: easy to define recursively
βt ( i ) = p ( ot +1ot +2 ...oT | qt = si ) βT ( i ) = 1
N
βT ( i ) = 1 βt ( i ) = ∑ βt +1 ( j ) Tij E j ( ot +1 )
N j =1
βt ( i ) = ∑ p ( ot +1 ∧ ot +2 ...oT ∧ qt +1 = s j | qt = si )
j =1
N
= ∑ p ( ot +1 ∧ qt +1 = s j | qt = si ) p ( ot + 2 ...oT | ot +1 ∧ qt +1 = s j ∧ qt = si )
j =1
N
= ∑ p ( ot +1 ∧ qt +1 = s j | qt = si ) p ( ot + 2 ...oT | qt +1 = s j )
j =1
N
= ∑ βt +1 ( j ) Tij E j ( ot +1 )
j =1
28/03/2011 Markov models 84

85. Max likelihood for HMMs
• The probability of traversing a certain arc at time t given
o1o2...oT:
ε ij ( t ) = p ( qt = si ∧ qt +1 = s j | o1o2 …oT )
p ( qt = si ∧ qt +1 = s j ∧ o1o2 …oT )
=
p ( o1o2 …oT )
p ( o1o2 … ot ∧ qt = si ) p ( qt = si ∧ qt +1 = s j ) p ( ot +1ot + 2 …oT | qt = si )
= N
∑ p ( o o …o ∧ q
i =1
1 2 t t = si ) p ( ot +1ot + 2 … oT | qt = si )
α t ( i ) Tij β t ( i )
ε ij ( t ) = N
∑α (i ) β (i )
i =1
t t
28/03/2011 Markov models 85

86. Max likelihood for HMMs
• The probability of being at state si at time t given o1o2...oT:
γ i ( t ) = p ( qt = si | o1o2 …oT )
N
= ∑ p ( qt = si ∧ qt +1 = s j | o1o2 …oT )
j =1
N
γ i ( t ) = ∑ ε ij ( t )
j =1
28/03/2011 Markov models 86

87. Max likelihood for HMMs
• Sum over the time index:
– Expected # of transitions from state i to j in o1o2...oT:
T −1
∑ ε (t )
t =1
ij
– Expected # of transitions from state i in o1o2...oT :
T −1 T −1 N N T −1
∑ γ ( t ) = ∑∑ ε ( t ) = ∑ ∑ε ( t )
t =1
i
t =1 j =1
ij
j =1 t =1
ij
28/03/2011 Markov models 87

88. Π = {π i } = { p ( q1 = si )}
Update parameters {
T = {Tij } = p ( qt +1 = s j | qt = si ) }
E = {E } = { p ( o = x
ij t j | q = s )}
t i
π i = expected frequency in state i at time t = 1 = γ i (1)
ˆ
T −1 T −1
expected # of transitions from state i to j ∑ ε (t )
t =1
ij ∑ ε (t )
t =1
ij
Tij = = T −1
= N T −1
expected # of transitions from state i
∑ γ ( t ) ∑∑ ε ( t )
t =1
i
j =1 t =1
ij
expected # of transitions from state i with x k observed
Eik =
expected # of transitions from state i
T −1 N T −1
∑ δ ( o , x ) γ ( t ) ∑∑ δ ( o , x ) ε ( t )
t =1
t k i
j =1 t =1
t k ij
= T −1
= N T −1
∑ γ (t )
t =1
i ∑∑ ε ( t )
j =1 t =1
ij
28/03/2011 Markov models 88

89. The inner loop of Forward-Backward
Given an input sequence.
1. Calculate forward probability:
– Base case: α1 ( i ) = Ei ( o1 ) π i
– Recursive case: α t +1 ( i ) = Ei ( ot +1 ) ∑ T jiα t ( j )
j
2. Calculate backward probability:
– Base case: βT ( i ) = 1
N
– Recursive case: βt ( i ) = ∑ βt +1 ( j ) Tij E j ( ot +1 )
j =1
α t ( i ) Tij βt ( i )
3. Calculate expected count: ε ij ( t ) = N
4. Update parameters: ∑α (i ) β (i )
i =1
t t
T −1 N T −1
∑ ε ij ( t ) ∑∑ δ ( o , x ) ε ( t )
j =1 t =1
t k ij
t =1
Tij = N T −1
Eik = N T −1
∑∑ ε ( t )
j =1 t =1
ij ∑∑ ε ( t )
j =1 t =1
ij
28/03/2011 Markov models 89

90. Forward-Backward: EM for HMM
• If we knew Φ we could estimate expectations of quantities
such as
– Expected number of times in state i
– Expected number of transitions i j
• If we knew the quantities such as
– Expected number of times in state i
– Expected number of transitions i j
we could compute the max likelihood estimate of Φ = 〈T, E, Π〉
• Also known (for the HMM case) as the Baum-Welch algorithm.
28/03/2011 Markov models 90

91. EM for HMM
• Each iteration provides values for all the parameters
• The new model always improve the likeliness of the
training data:
( ˆ )
p o1o2 …oT | Φ ≥ p ( o1o2 …oT | Φ )
• The algorithm does not guarantee to reach global
maximum.
28/03/2011 Markov models 91

92. EM for HMM
• Bad News
– There are lots of local minima
• Good News
– The local minima are usually adequate models of the data.
• Notice
– EM does not estimate the number of states. That must be given (tradeoffs)
– Often, HMMs are forced to have some links with zero probability. This is done
by setting Tij = 0 in initial estimate Φ(0)
– Easy extension of everything seen today: HMMs with real valued outputs
28/03/2011 Markov models 92

93. Contents
• Introduction
• Markov Chain
• Hidden Markov Models
• Markov Random Field (from the viewpoint of
classification)
28/03/2011 Markov models 93

94. Example: Image segmentation
• Observations: pixel values
• Hidden variable: class of each pixel
• It’s reasonable to think that there are some underlying relationships
between neighbouring pixels... Can we use Markov models?
• Errr.... the relationships are in 2D!
28/03/2011 Markov models 94

95. MRF as a 2D generalization of MC
• Array of observations: X = { xij } , 0 ≤ i < Nx , 0 ≤ j < N y
• Classes/States: S = {sij } , sij = 1...M
• Our objective is classification: given the array of
observations, estimate the corresponding values of the
state array S so that
p( X | S ) p(S ) is maximum.
28/03/2011 Markov models 95

96. 2D context-dependent classification
• Assumptions:
– The values of elements in S are mutually dependent.
– The range of this dependence is limited within a neighborhood.
• For each (i, j) element of S, a neighborhood Nij is defined so
that
– sij ∉ Nij: (i, j) element does not belong to its own set of neighbors.
– sij ∈ Nkl ⇔ skl ∈ Nij: if sij is a neighbor of skl then skl is also a neighbor
of sij
28/03/2011 Markov models 96

97. 2D context-dependent classification
• The Markov property for 2D case:
( )
p sij | Sij = p ( sij | N ij )
where Sij includes all the elements of S except the (i, j) one.
• The elegeant dynamic programing is not applicable: the problem is
much harder now!
28/03/2011 Markov models 97

98. 2D context-dependent classification
• The Markov property for 2D case:
( )
p sij | Sij = p ( sij | N ij )
where Sij includes all the elements of S except the (i, j) one.
We are gonna see an
• The elegeant dynamic programing is not applicable: the problem is
application of MRF for
much harder now! Image Segmentation
and Restoration.
28/03/2011 Markov models 98

99. MRF for Image Segmentation
• Cliques: a set of each pixel which are neighbors
of each other (w.r.t the type of neighborhood)
28/03/2011 Markov models 99

100. MRF for Image Segmentation
• Dual Lattice number
• Line process:
28/03/2011 Markov models 100

101. MRF for Image Segmentation
• Gibbs distribution:
1 −U ( s )
π ( s ) = exp
Z T
– Z: normalizing constant
– T: parameter
• It turns out that Gibbs distribution implies MRF
([Gema 84])
28/03/2011 Markov models 101

102. MRF for Image Segmentation
• A Gibbs conditional probability is of the form:
1  1 
p ( sij | N ij ) = exp  − ∑ Fk ( Ck ( i, j ) ) 
Z  T k 
– Ck(i, j): clique of the pixel (i, j)
– Fk: some functions, e.g.
1
(
− sij α1 + α 2 ( si −1, j + si +1, j ) + α 2 ( si , j −1 + si , j +1 )
T
)
28/03/2011 Markov models 102

103. MRF for Image Segmentation
• Then, the joint probability for the Gibbs model is
 ∑∑ Fk ( Ck ( i, j ) ) 
 i, j k 
p ( S ) = exp  − 
 T 
 
– The sum is calculated over all possible cliques associated
with the neighborhood.
• We also need to work out p(X|S)
• Then p(X|S)p(S) can be maximized... [Gema 84]
28/03/2011 Markov models 103

104. More on Markov models...
• MRF does not stop there... Here are some related models:
– Conditional random field (CRF)
– Graphical models
– ...
• Markov Chain and HMM does not stop there...
– Markov chain of order m
– Continuous-time Markov chains...
– Real-value observations
– ...
28/03/2011 Markov models 104

105. What you should know
• Markov property, Markov Chain
• HMM:
– Defining and computing αt(i)
– Viterbi algorithm
– Outline of the EM algorithm for HMM
• Markov Random Field
– And an application in Image Segmentation
– [Geman 84] for more information.
28/03/2011 Markov models 105

106. Q&A
28/03/2011 Markov models 106

107. References
• L. R. Rabiner, "A Tutorial on Hidden Markov Models and Selected Applications
in Speech Recognition“, Proc. of the IEEE, Vol.77, No.2, pp.257--286, 1989.
• Andrew W. Moore, “Hidden Markov Models”, http://www.autonlab.org/tutorials/
• Geman S., Geman D. “Stochastic relaxation, Gibbs distributions and the
Bayesian restoration of images,” IEEE Transactions on Pattern Analysis and
Machine Intelligence, Vol. 6(6), pp. 721-741, 1984.
28/03/2011 Markov models 107