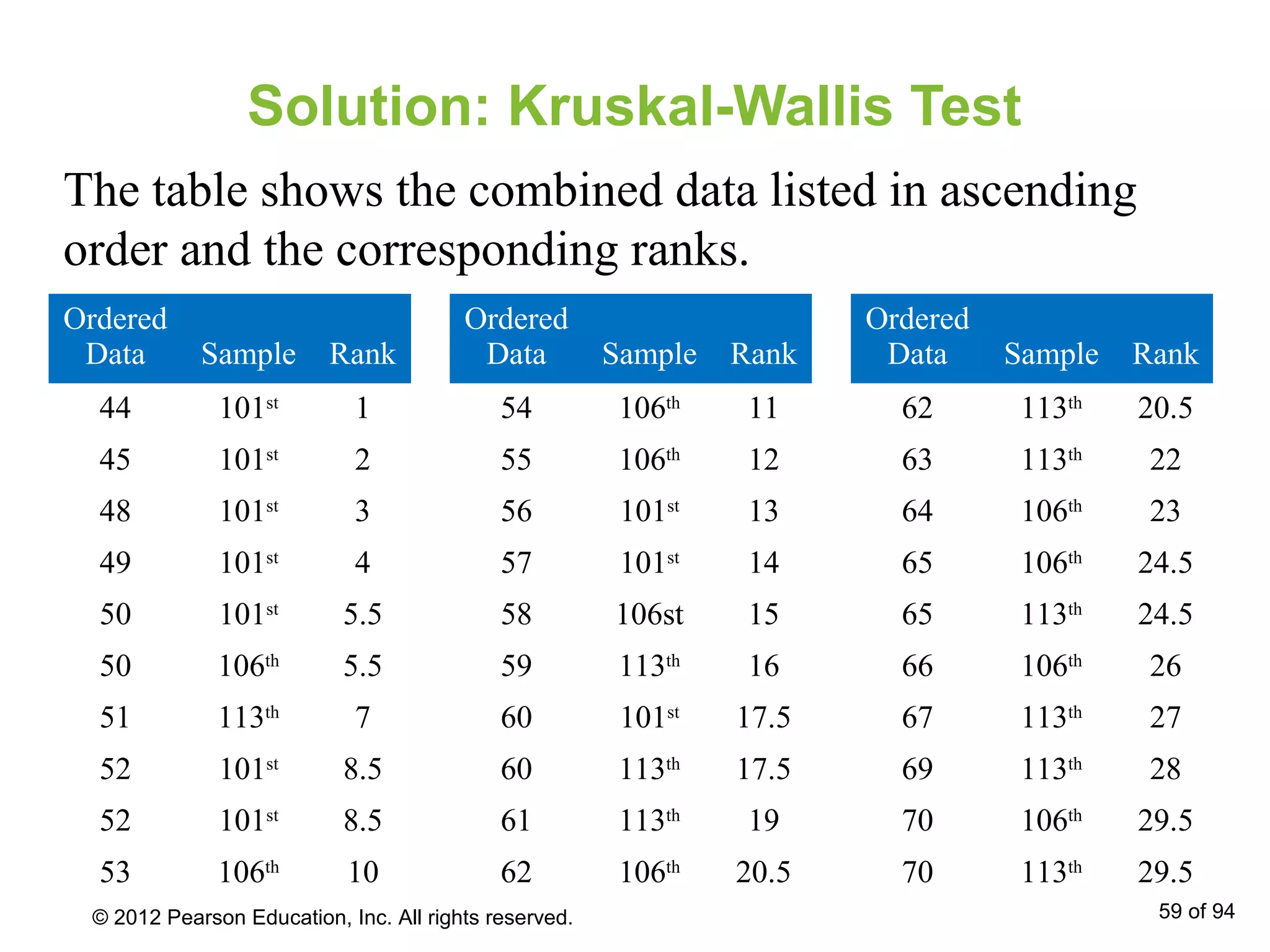
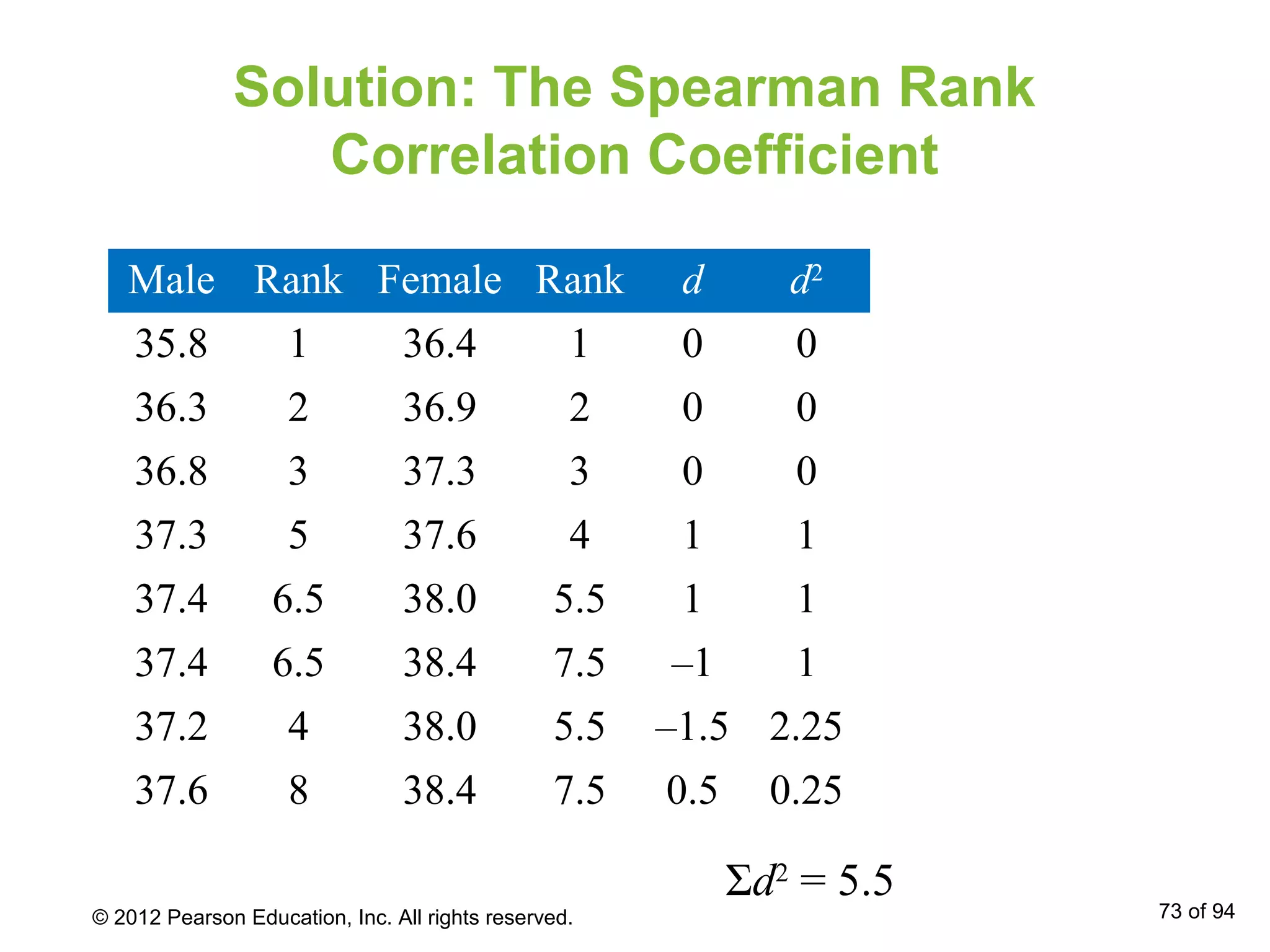
This document provides an overview of nonparametric tests, including the sign test and Wilcoxon tests. It discusses how to perform the sign test to test a population median and the paired sample sign test. It also reviews how to conduct the Wilcoxon signed-rank test to compare two dependent samples and determine if they come from populations with the same distribution. Examples are provided to demonstrate how to apply these nonparametric tests and interpret the results.